관계(2)
(1) 서술식방법
(2) 나열식 방법
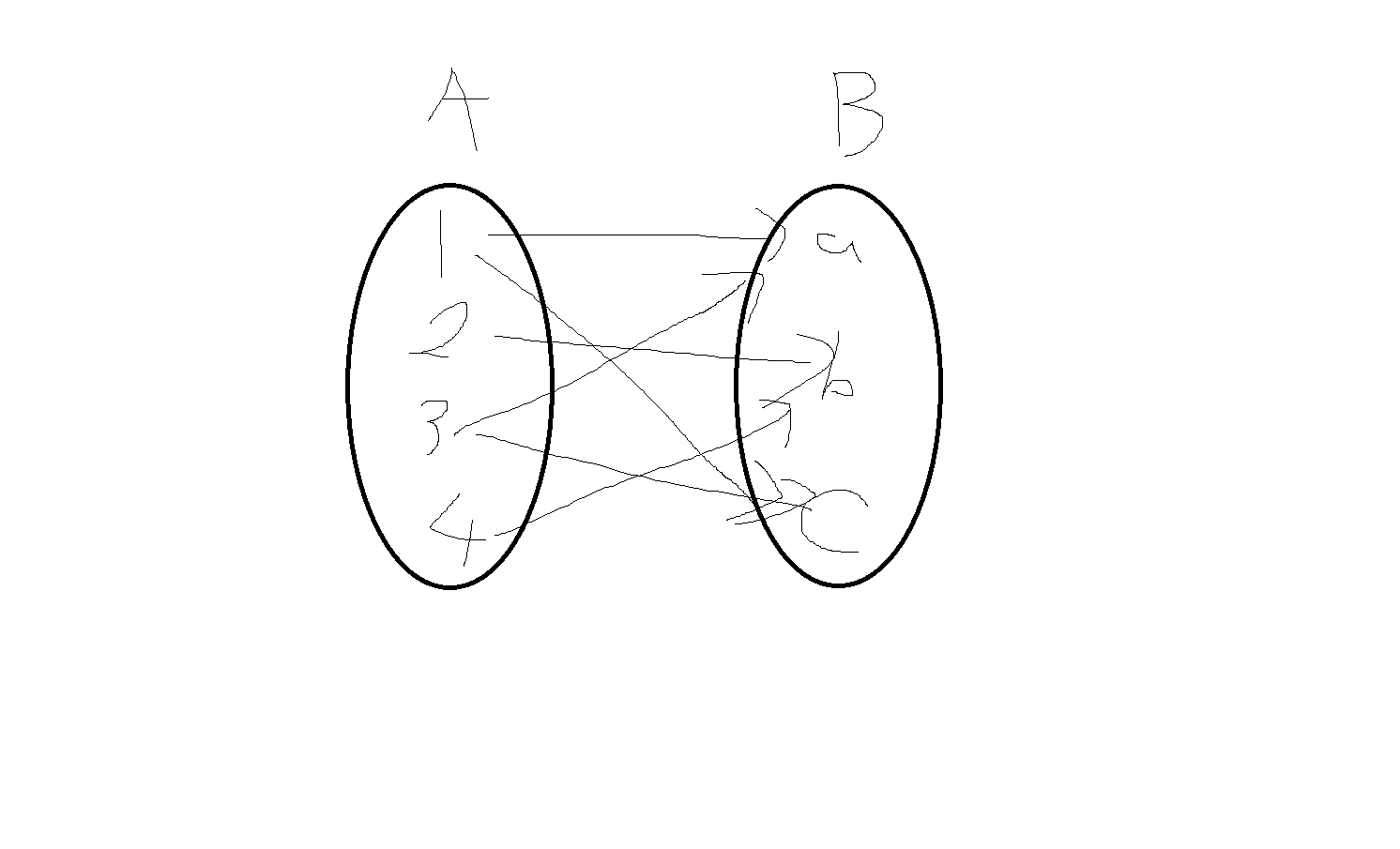
(1) 화살표 도표
집합 A에 속하는 a. 집합 B에 속하는 b
예제 5-8) 집합 A={1,2,3,4}, B={a,b,c}
R = {(1,a), (1,c), (2,b), (3,a), (3,c), (4,b)}
관계 R을 화살표 도표로 그려라
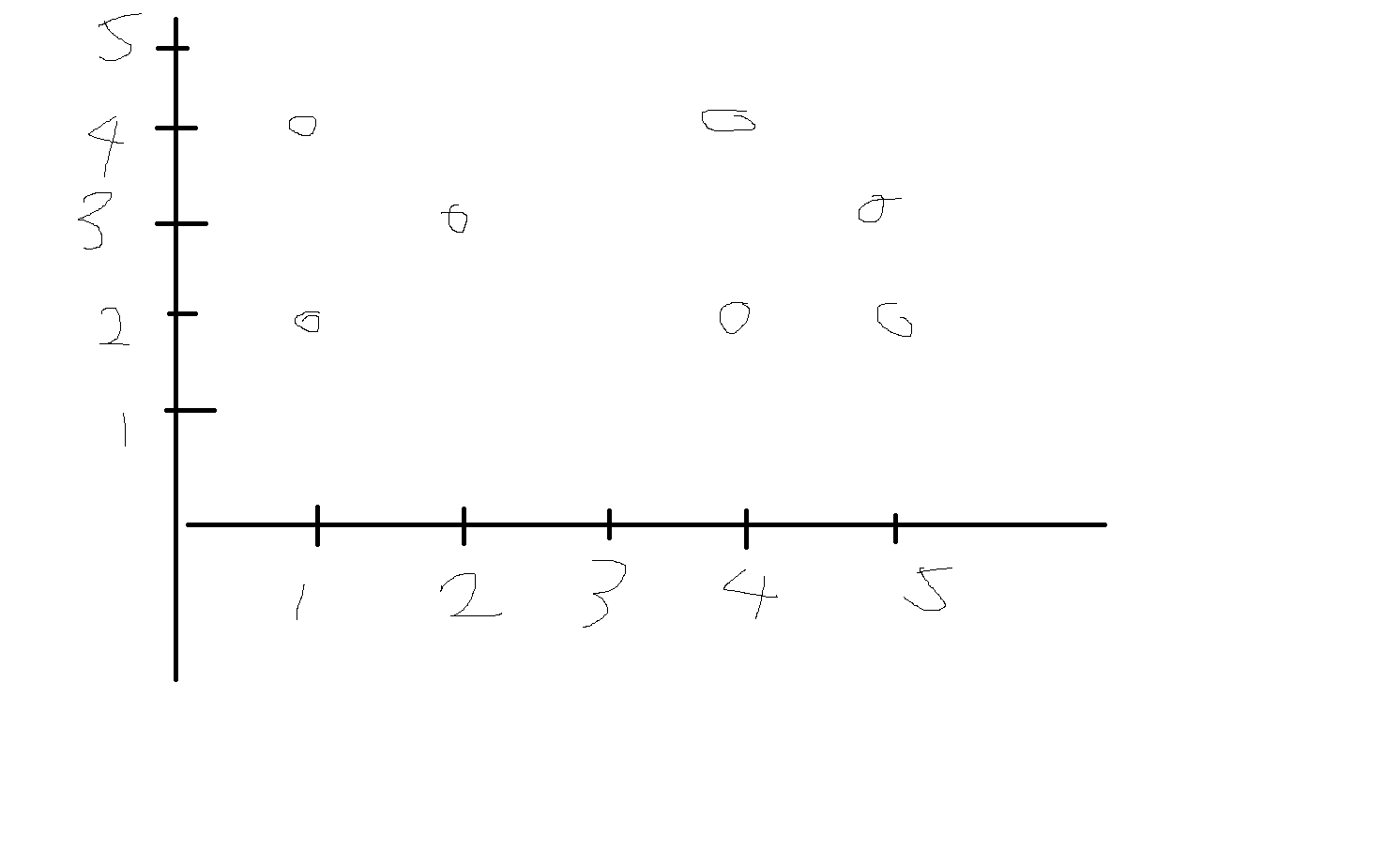
(2) 좌표도표
집합 A, B. a∈A, b∈B
예제 5-9) A={1,2,3,4,5}, B={2,3,4}이고 집합 A에서 집합 B로의 관계
R = {(1,2), (1,4), (2,3), (4,2), (4,4), (5,2), (5,3)}
관계 R을 좌표도표를 이용하여 표시해라.
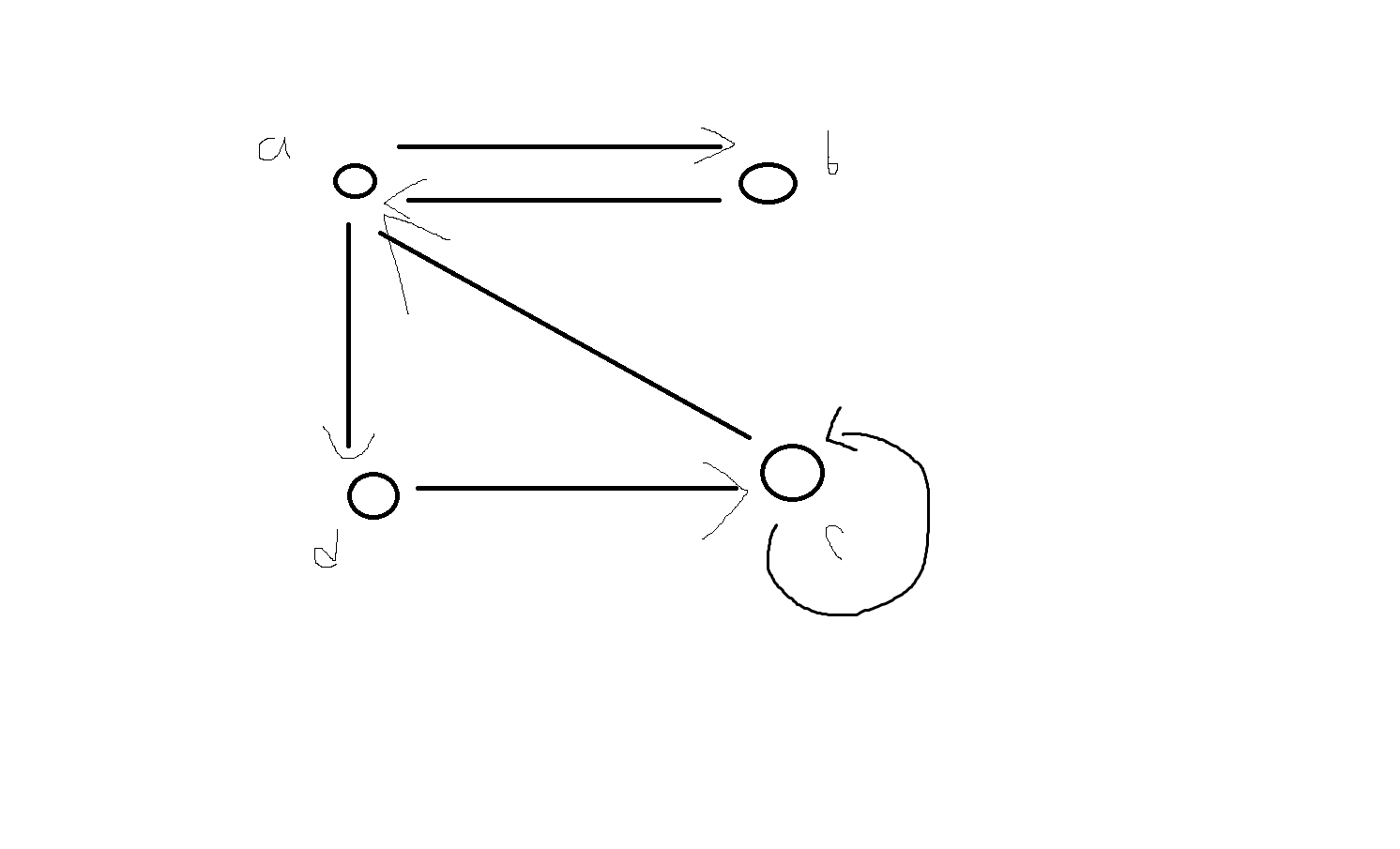
(3) 방향 그래프
G = (V, E)
Graph = (Vertex, Edge)
에제 5-10) R = {(a,b), (b,a), (a,d), (d,c), (c,c), (c,a)}
R을 방향그래프로 그리시오
예제 5-11) 관계 R에 대한 방향그래프가 다음과 같은때 관계 R의 순서쌍을 구해보자
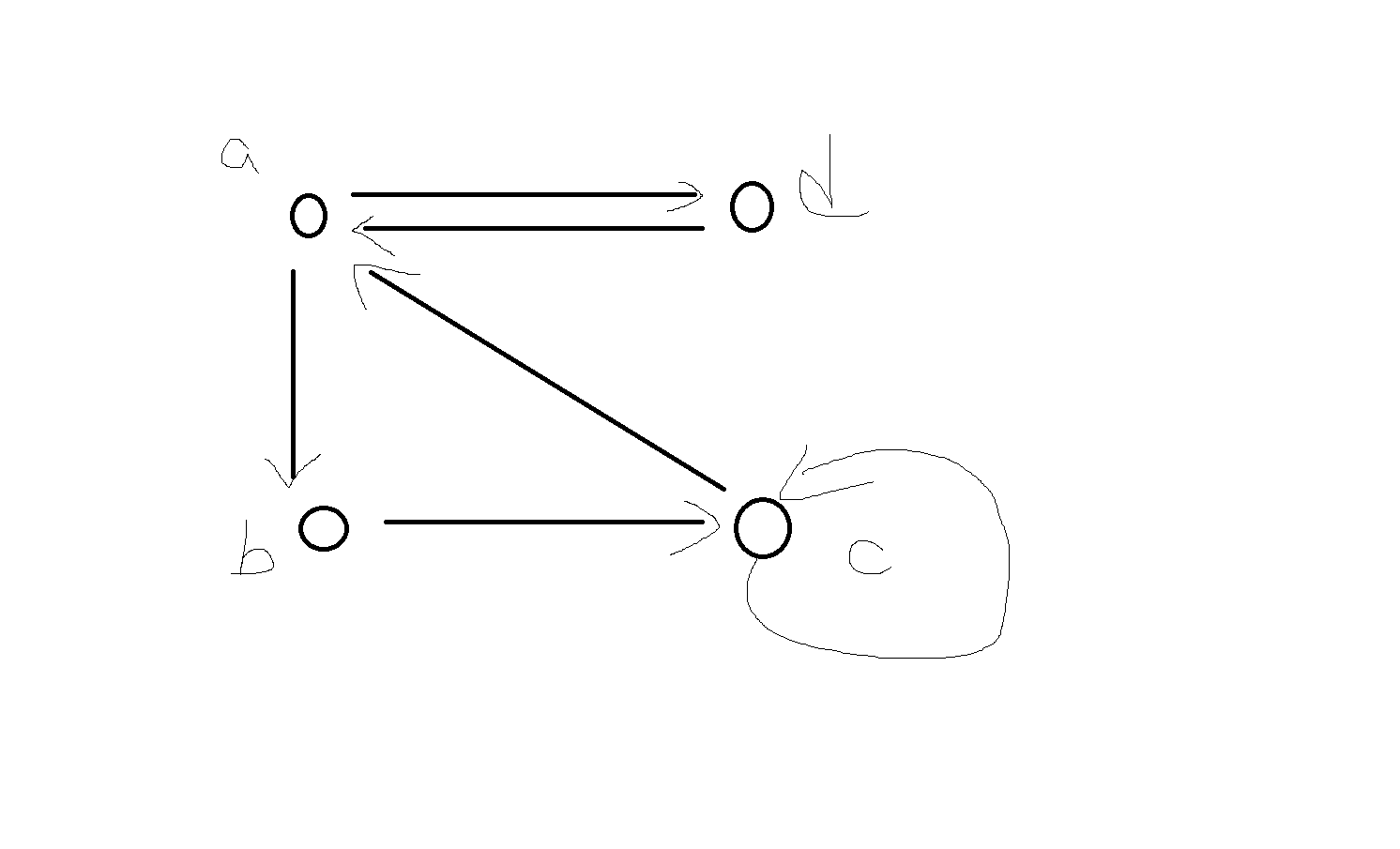
R = {(a,d), (d,a), (a,b), (b,c), (c,c), (c,a)}
(4) 관계행령 (부울행렬)
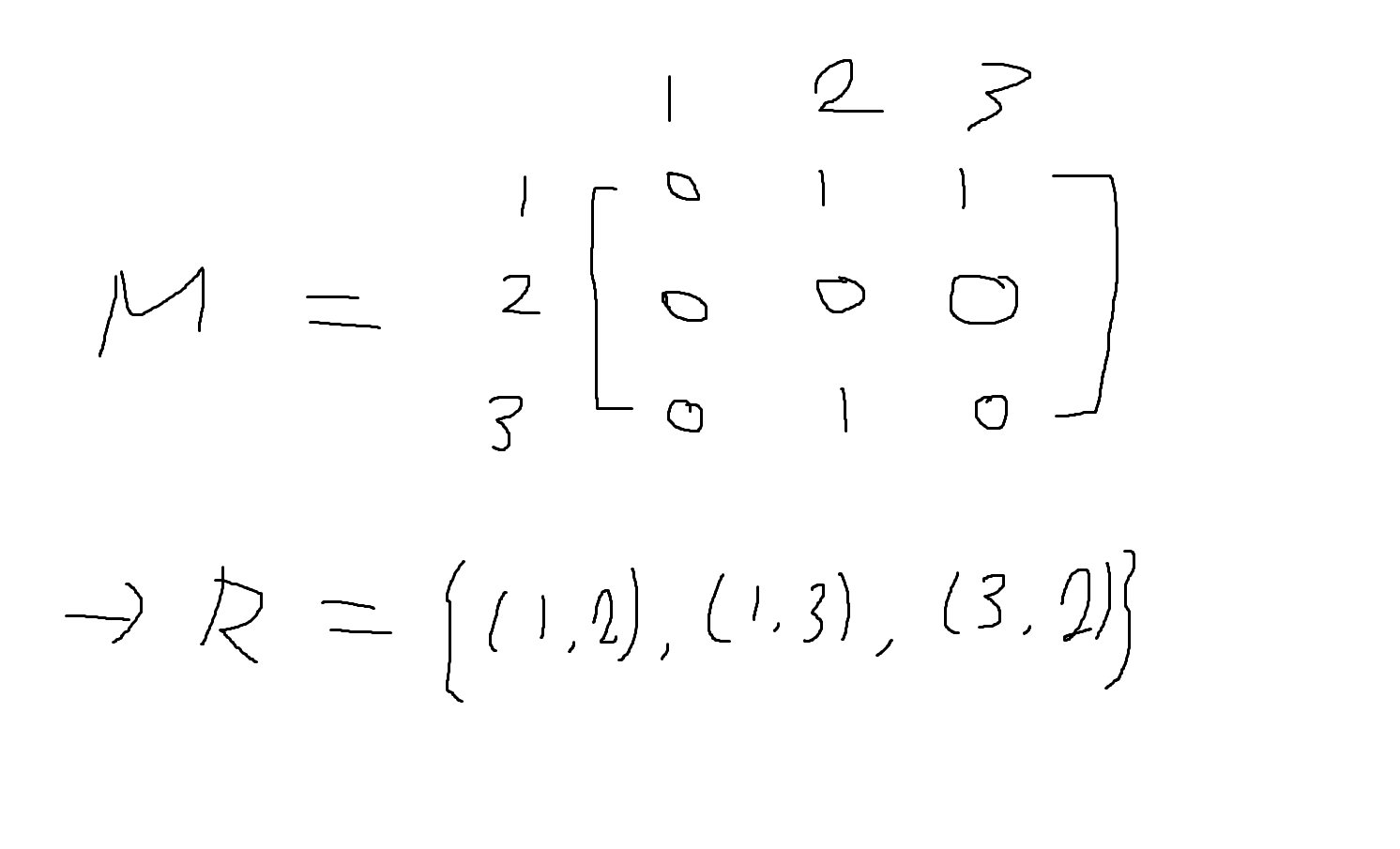
M[i,j] = 1 if (ai, bi) ∈ R, 0 if (ai, bi) !∈ R
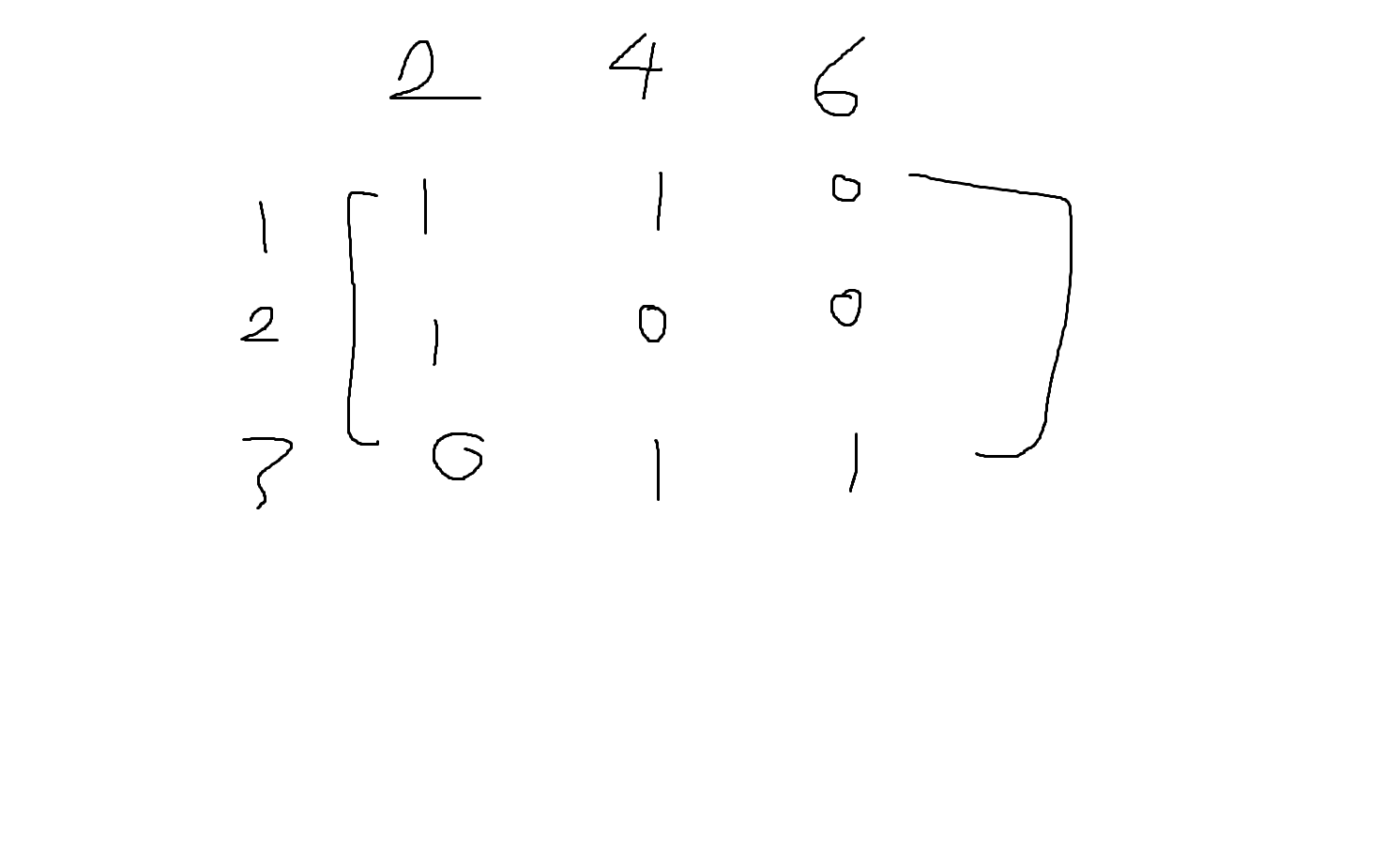
예제 5-12 집합 A={1,2,3}, B={2,4,6}에 대한 관계 R의 순서쌍들의 집합이 다음과 같을 때 관계 R을 관계행렬로 표현해보자.
R={(1,2), (1,4), (2,2), (3,4), (3,6)}
정의 5-4. 세 집합 A,B,C에서 R₁을 집합 A에서 집합 B로의 관계라 하고, R₂를 집합 B에서 집합 C로의 관계라 하면, 집합 A에서 집합 C로의 합성관계 R₁ R₂ 또는 R₁ R₂는 다음과 같이 정의된다.
R₁* R₂ = {(a,c)|a∈A, c∈C, {a,b}∈R₁이고 (b,c)∈R₂}
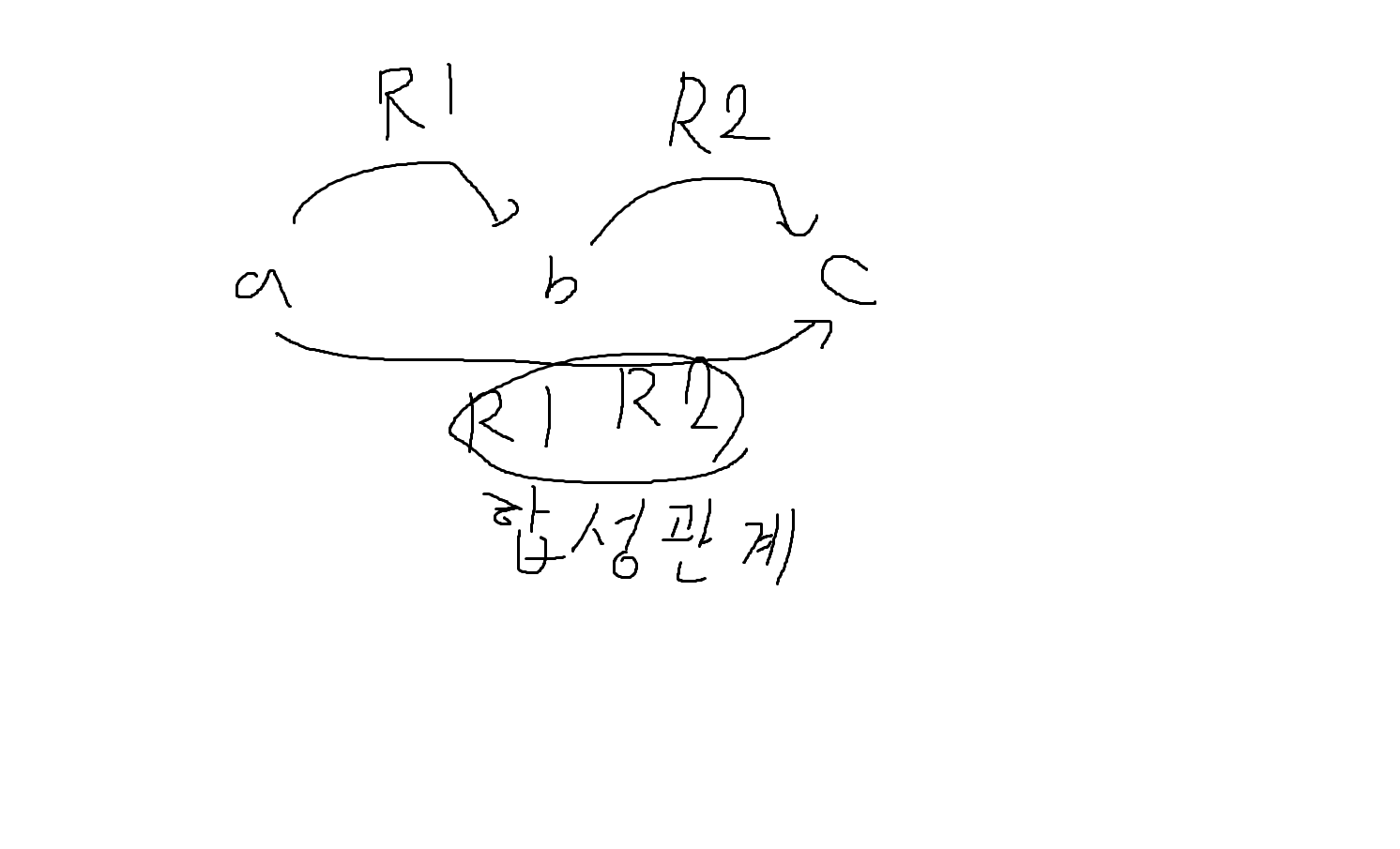
- 합성관계는 주어진 두 관계로부터 새로운 관계를 이끌어낸다.
- 이미 존재하고 있는 관계 R₁과 R₂로부터 새로운 관계 R₁* R₂를 만들어냄
예제5-14) 집합 A,B,C가 각각 A={1,2,3,4}, B={a,b,c}, C={x,y,z}이고 집합 A에서 집합 B로의 관계를 R, 집합 B에서 C로의 관계를 S라 한다. R과 S가 다음과 같을 때 R*S를 나타내라.
R={(1,a),(1,b),(2,b),(3,a),(4,b),(4,c)}
S={(a,x),(b,y),(c,x),(c,z)}
R * S = {(1,x), (1,y), (2,y), (3,x), (4,y), (4,x), (4,z)}
예제 5-15. 5-14를 관계행렬로 나타내라.
R={(1,a),(1,b),(2,b),(3,a),(4,b),(4,c)}
S={(a,x),(b,y),(c,x),(c,z)}
R
| a | b | c | |
|---|---|---|---|
| 1 | 1 | 1 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 0 | 0 |
| 4 | 0 | 1 | 1 |
S
| x | y | z | |
|---|---|---|---|
| a | 1 | 0 | 0 |
| b | 0 | 1 | 0 |
| c | 1 | 0 | 1 |
RS
| x | y | z | |
|---|---|---|---|
| 1 | 1 | 1 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 0 | 0 |
| 4 | 1 | 1 | 1 |
정의 5-5. 집합 A에 대한 항등관계 (identity relation) IA는 다음과 같이
IA = {(a,a)|a∈A}
IAR = RIB = R
항등관계를 이용한 합성관계는 원래의 관계와 같음.
연습문제
1) A={1,2,3,4}, B={1,2,3,4}이고 집합 A에서 집합 B로의 관계가 R과 S로 나타내어진다.
R = {(1,2), (1,3), (2,2), (3,1), (4,2)}
S = {(1,1), (1,3), (2,3), (3,3), (4,1), (4,4)}
이 경우 다음을 구하시오
가) IAR
-> R과 같다.
나) RS
1->2->3
1->3->3
2->2->3
3->1->1
3->1->3
4->2->3
RS = {(1,3), (2,3), (3,1), (3,3), (4,3)}
예제 5-17. A={1,2,3,4}, B={1,2,3}이고 A->B 관계 R
R = {(1,2), (1,3), (2,2), (3,1), (4,2)}
(1) IAR
R과 동일
(2) IB = {(1,1), (2,2), (3,3)}
요약
- 관계표현 (화살표도표, 좌표도표, 방향 그래프, 관계행렬)
- 세 집합 A,B,C에서의 합성 관계 R1 R2또는 R1 R2는 다음과 같이 정의
R1 * R2 = {(a,c)| a∈A, c∈C, (a,b)∈R1이고 (b,c)∈R2}
