확률변수의 쌍 (3)
- T/F 확인문제
(1) Fx,y(x,y)가 두 확률변수 X, Y의 결합누적분포함수 (joint CDF)일 때, X의 한계확률밀도함수(marginal PDF)는 fx(x) = d/dx [lim y->∞ Fx,y(x,y)]이다.
y -> ∞
Fx,y(x,y) = Fx,y(x,∞) = Fx(x)
d/dx Fx(x) = fx(x)
-> T
(2) Fx,y(x, y)는 두 확률변수 X, Y의 결합누적분포함수 (joint CDF)이고, 상수 x₁, x₂, y₁, y₂는 x₁< x₂, y₁< y₂을 만족할 때, P[x₁ < X <= x₂, y₁ < Y <= y₂] = Fx,y(x₂, y₂) - Fx,y(x₁, y₁)이다.
-> F
Fx(x) = A - B (하나의 값일 때는 양쪽 끝값으로 되지만)
(x, y) 두개의 값이면 양쪽 끝값만으로는 안된다.
-
(복습) 모멘트 (moment)
확률변수 X의 특성을 나타내는 여러 지표(평균, 분산)와 관련된 정보
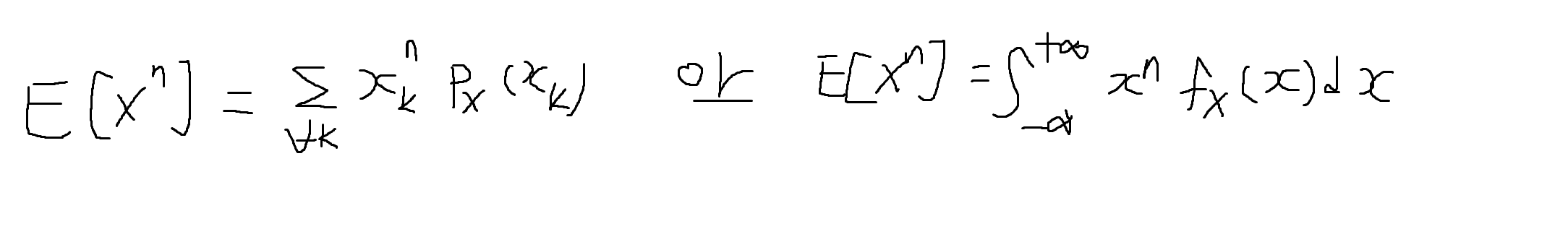
-
우리는 기대값과 분산을 구하기 위한 용도로 학습 (n = 1, 2) : E[X¹], E[X²]
-
두 확률변수를 생각할 때, 모멘트? 결합모멘트 (joint moment)
-
두 확률변수의 결합 모멘트를 공부하기에 앞서...
-
Y = g(x)일때, Y의 기대값? (확률변수함수의 기대값)
E[g(x)] = ∫-∞ to +∞ g(x) fx(x) dx
- g(x) = X^n의 형태의 경우가 확률변수의 모멘트
E[X^n] = ∫(x^n) fx(x) dx
1) "두 확률변수 함수"의 기대값 : Z = g(X,Y)
2) 두 확률변수의 결합모멘트
- 단일 확률변수에서 확률변수의 기대값 개념을 확장
E[Z] = E[g(x, y)]
= ∫∫g(x, y) fx,y(x,y) dx dy
" 두 확률변수함수"의 기대값
E[g(X, Y)] = ∫-∞ to +∞ ∫-∞ to +∞ g(x,y) fx,y(x,y) dx dy
- 단일확률변수에서 확률변수함수의 기대값 개념을 확장
예제 5-15 : 두 확률변수 X, Y의 결합확률밀도함수 (joint PDF)가 fx,y(x,y)일 때, Z = X + Y의 기대값을 구하여라
- 우리가 알고있는 E[X + Y] = E[X] + E[Y]가 나오는지 확인
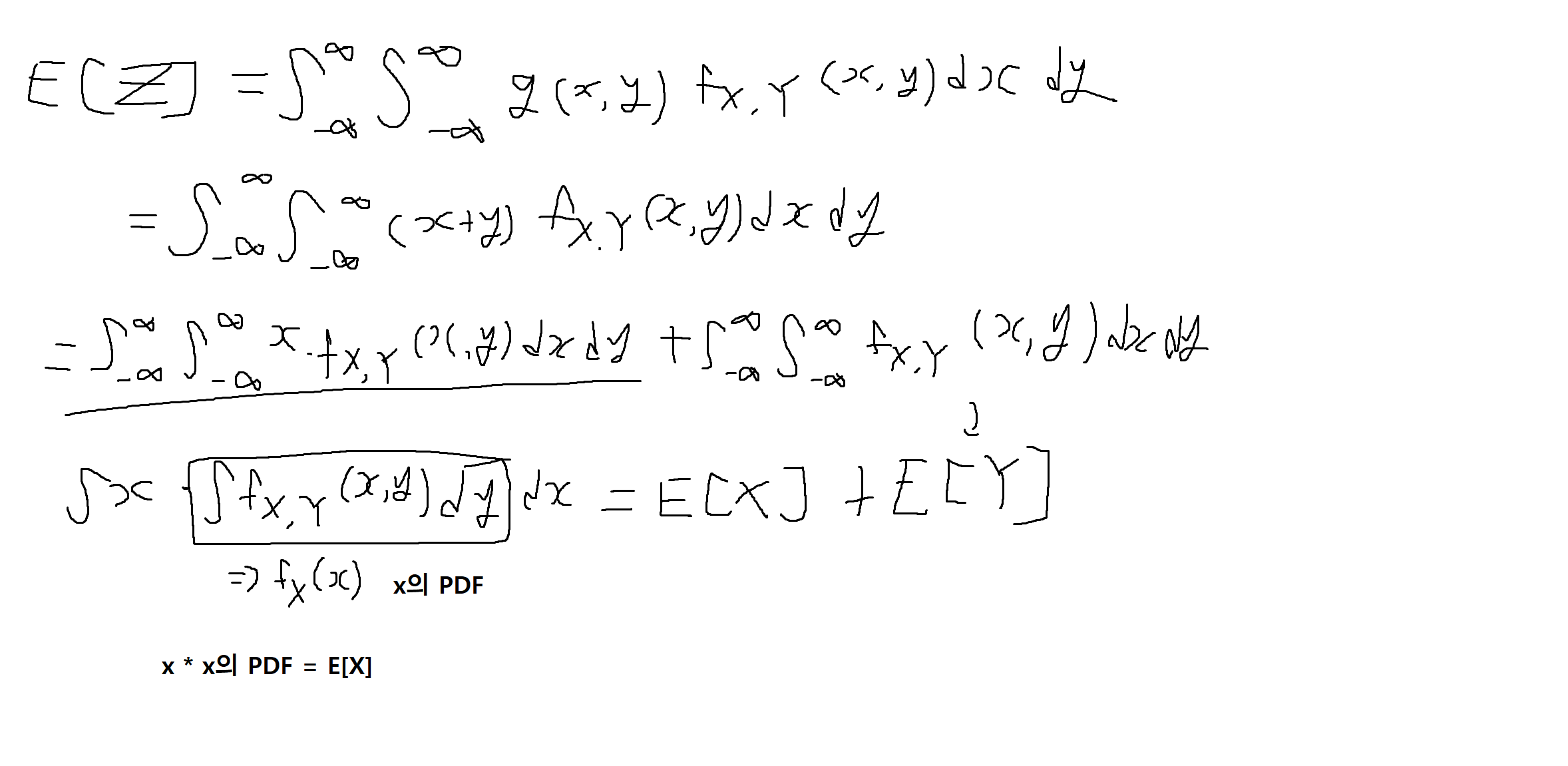
-
두 확률변수의 결합모멘트 (joint moment)
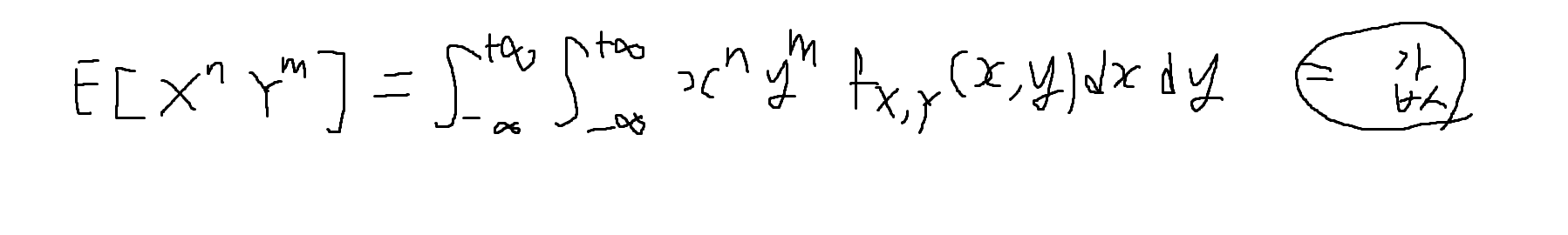
-
두 확률변수 X, Y의 결합성에 관한 정보
-
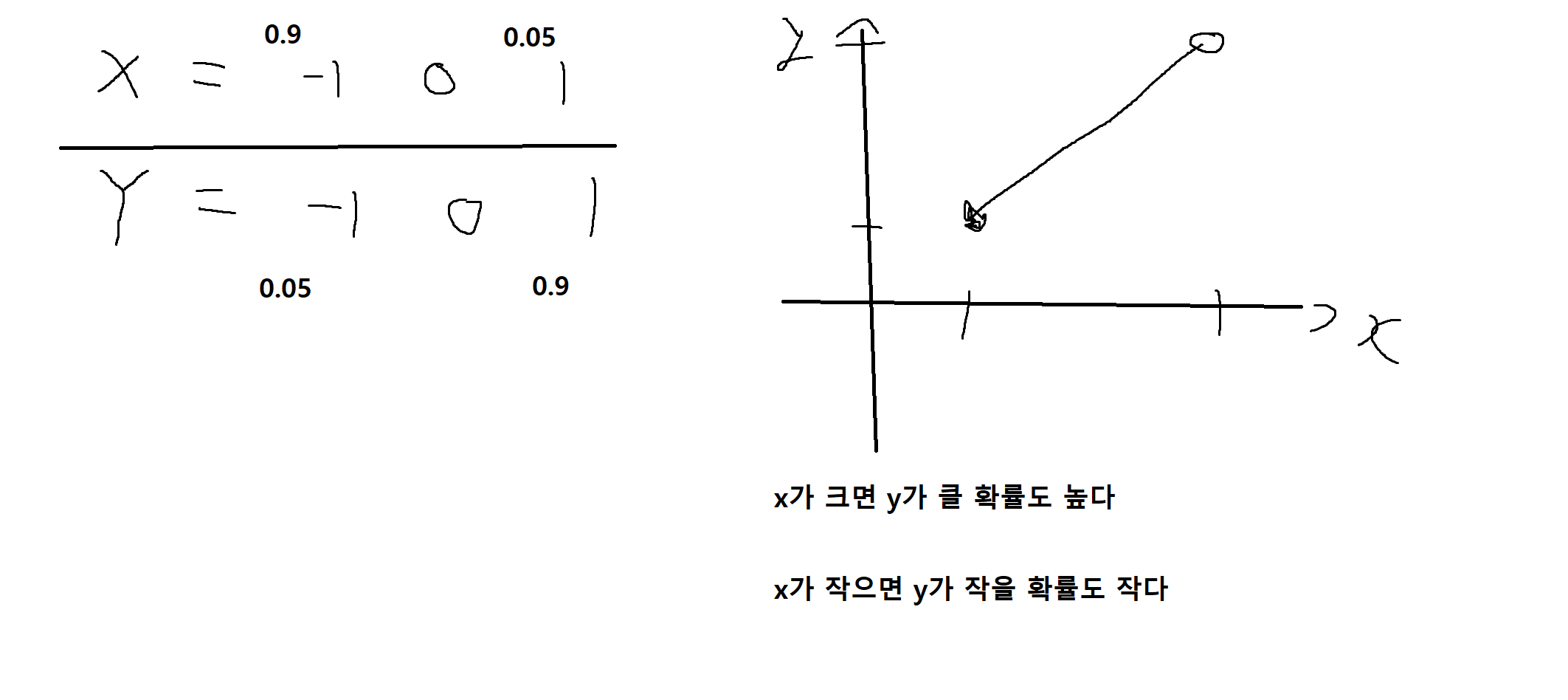
예를 들어 n = m = 1, E[XY]는 X, Y의 선형(linear) 관련성에 관한 척도
선형관련성 = x가 큰 값일 때 Y도 큰 값일 확률이 높냐, 작냐 -
단일확률변수와 비슷하게 단순한 절대수치보다 상대적 수치가 필요
-
공분산 (covariance) -> 절대
cov[X, Y] = E[(X - mx) (Y - mx) = E[XY] - E[X] * E[Y] -
상관계수 (correlation coefficient)
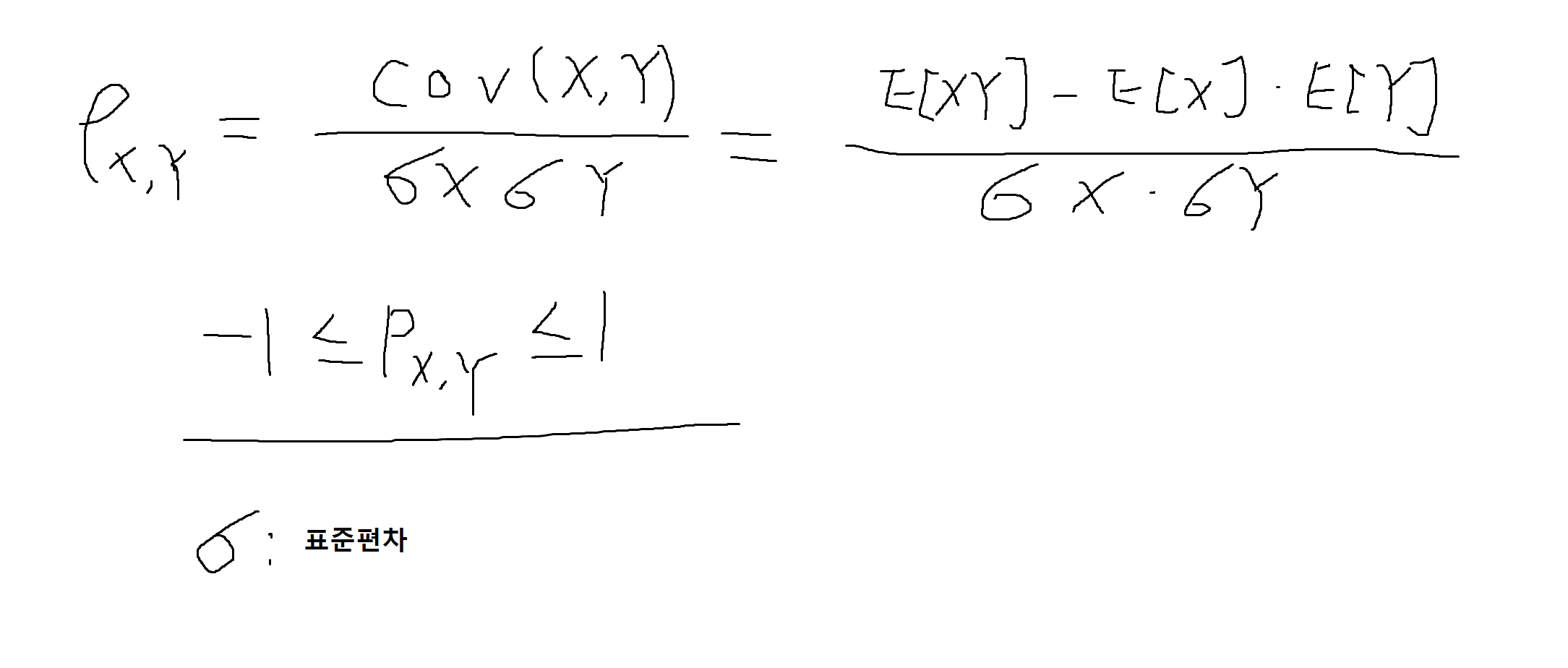
예제 5-16 : 두 확률변수 X, Y가 독립일 때 cov(X, Y)를 구하여라
독립 -> fx,y(x,y) = fx(x) * fy(y)
cov(X, Y) = E[XY] - E[X] * E[Y]

예제 5-17 : 두 확률변수 X, Y가 결합확률밀도함수 (joint PDF)가 다음과 같을 때, 독립, 비상관(uncorrelated) 여부를 판단하시오.
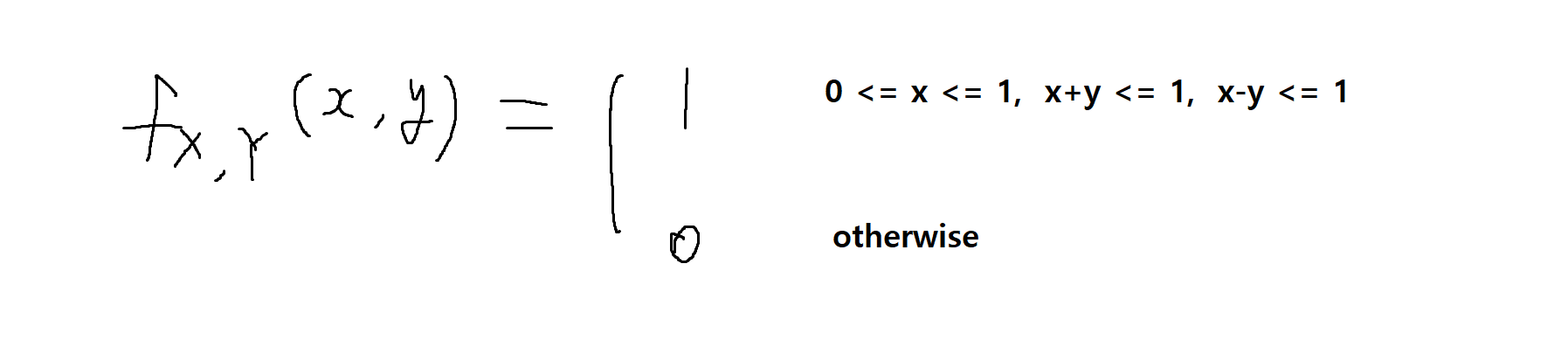
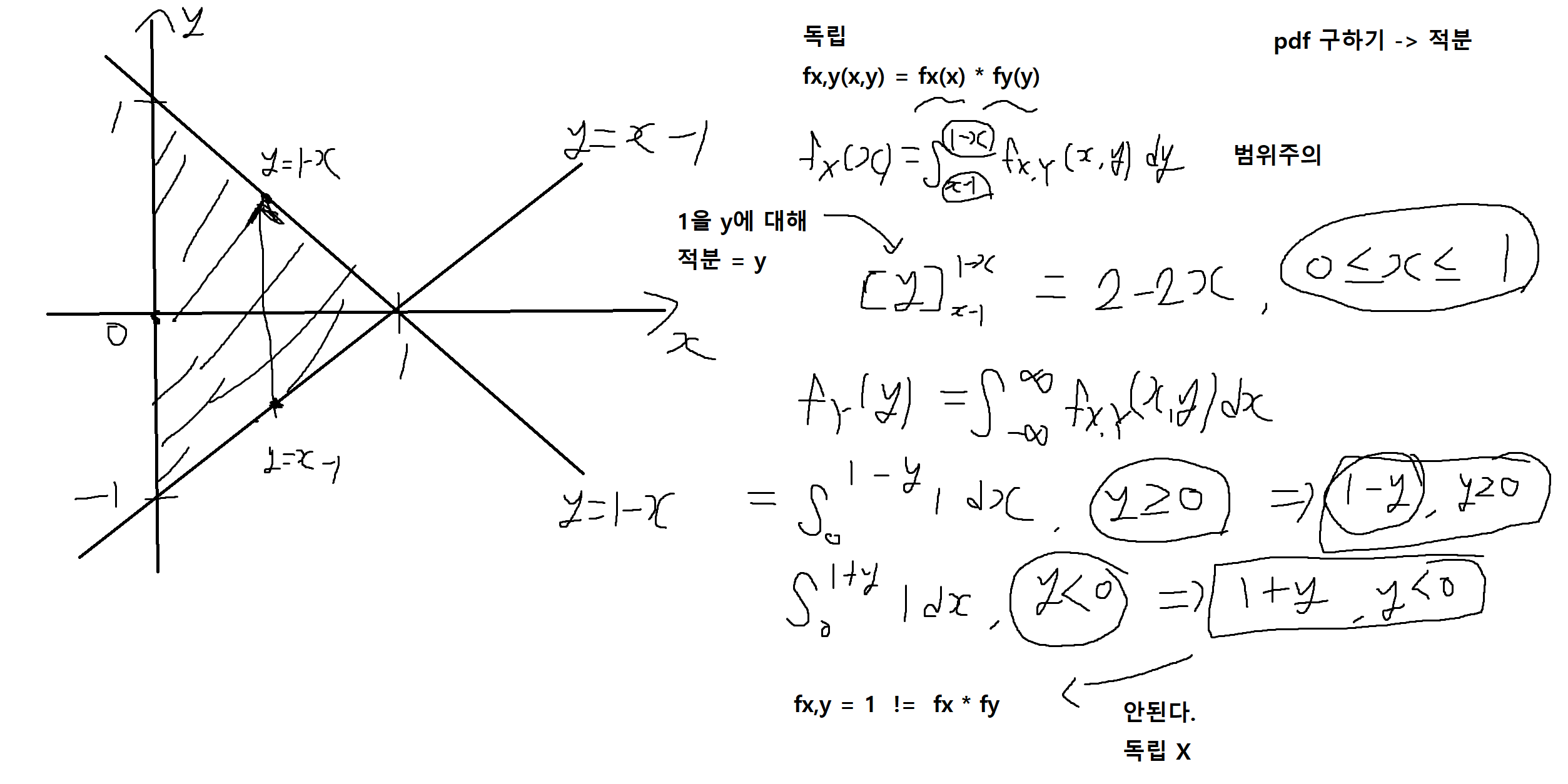

두 확률변수의 결합 모멘트
-
두 확률변수 X, Y의 결합성 관련척도 요약
-
E[XY]는 X, Y의 선형(linear) 관련성에 관한 척도 (절대적 수치)
-
E[XY] = 0이면 X와 Y는 직교 (orthogonal)
E[X^n * Y^m], n = 1, m = 1
-> 선형결합성 (하나가 클 때 다른 하나도 클 확률)
비상관 (uncorreltated) ρx,y = 0과 독립의 관계
(True) 두 확률변수 X, Y가 독립 (independent) -> ρx,y = E[XY] - E[X] * E[Y] = 0
(False) ρx,y = E[XY] - E[X] * E[Y] = 0
≠> 두 확률변수 X, Y가 독립 (independent)
비상관 ≠> 독립 (독립일 수도 있고 아닐 수도 있다.)
예제 5-18 : 확률변의 쌍 (X, Y)가 다음과 같은 결합확률질량함수를 갖을 때, 상관계수 (correlation coefficient)를 구하고 독립, 직교, 비상관 여부를 구해라
독립 E[XY] = E[X] E[Y]
직교 E[XY] = 0
비상관 E[XY] - E[X] E[Y] = 0
(a)
| X/Y | -1 | 0 | 1 |
|---|---|---|---|
| -1 | 1/6 | 0 | 1/6 |
| 0 | 0 | 1/3 | 0 |
| 1 | 1/6 | 0 | 1/6 |
ρx,y(0, -1) = ρx(0) ρy(-1)
0 != (1/3) (1/3)
-> 독립 X
E[XY] = ∑xy * Px,y(x,y)
= (-1)(-1)(1/6) + ...
= 1/6((-1)(-1) + (-1)(1) + (1)(-1) + (1)(1))
E[XY] = 0
=> 직교 O
cov = E[XY] - E[X]E[Y] = 0
ρx,y = cov(X, Y) / (σx * σy) = 0
=> 상관계수 == 0 (비상관)
(b)
| X/Y | -1 | 0 | 1 |
|---|---|---|---|
| -1 | 1/9 | 1/9 | 1/9 |
| 0 | 1/9 | 1/9 | 1/9 |
| 1 | 1/9 | 1/9 | 1/9 |
독립 O
직교 O
상관계수 == 0 (비상관)
결합 가우스 확률 변수
- (복습) 가우스 (정규) 확률변수
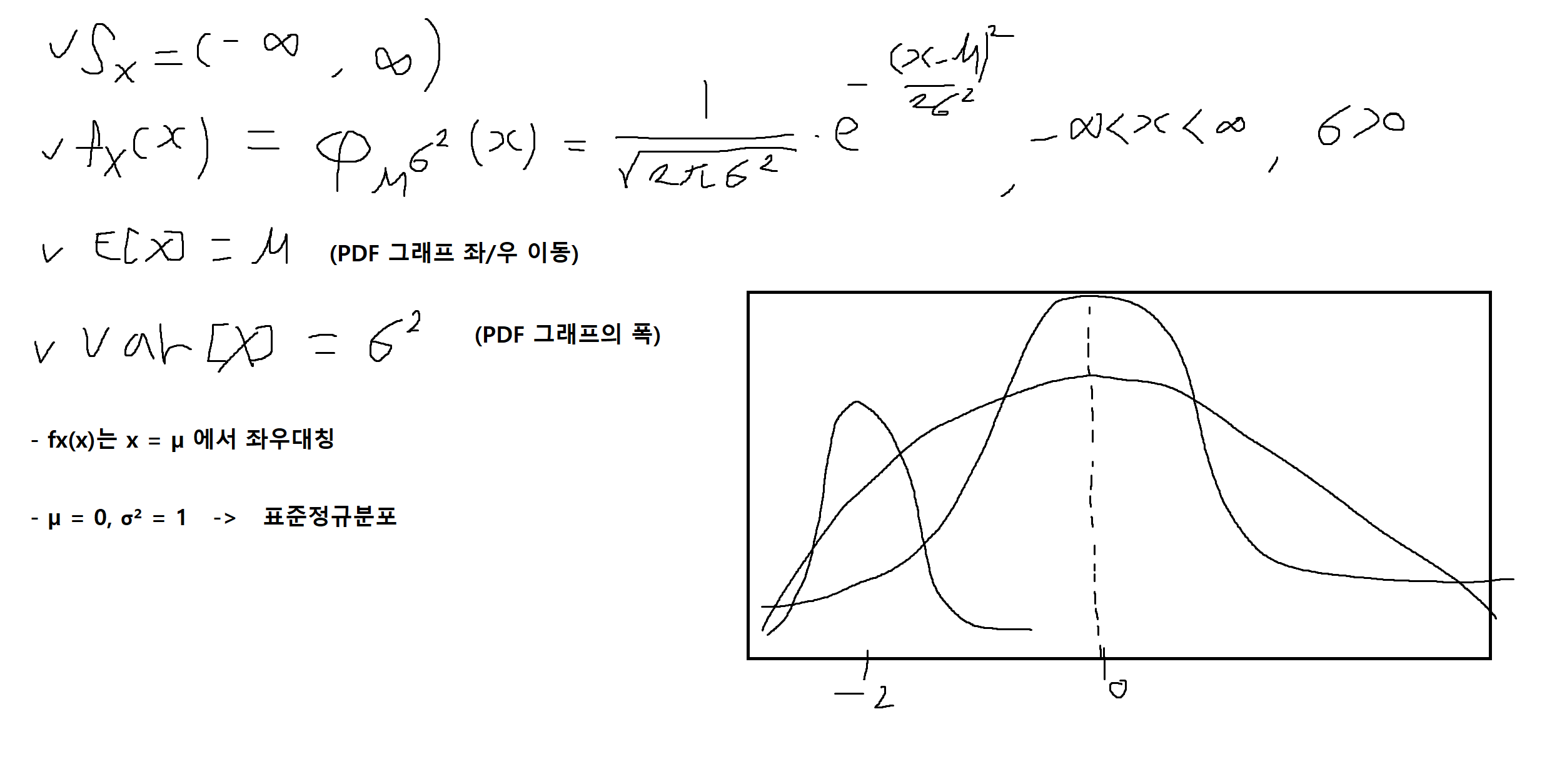
-
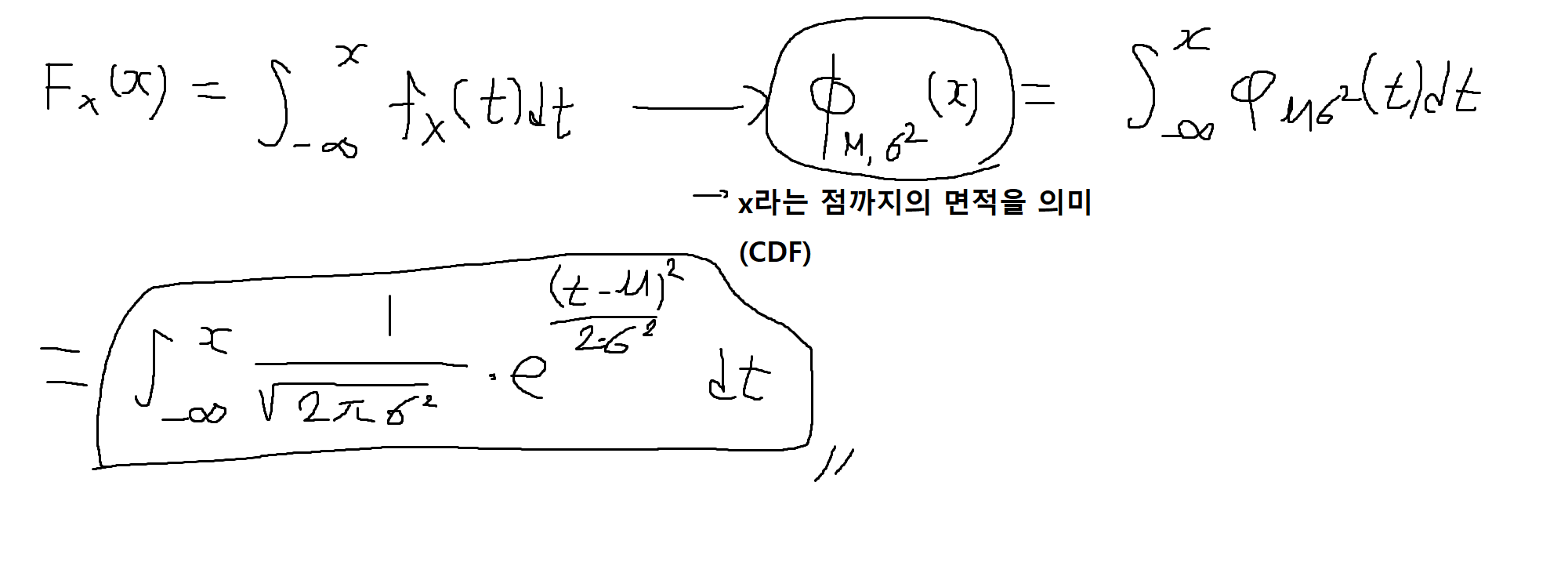
(복습) 가우스(정규) 확률변수의 CDF (확률변수 : X, 평균 : µ, 분산 : σ²)
-
다양한 평균(µ) / 분산(σ²) 조건 -> 표준정규분포 z 변환해서 생각
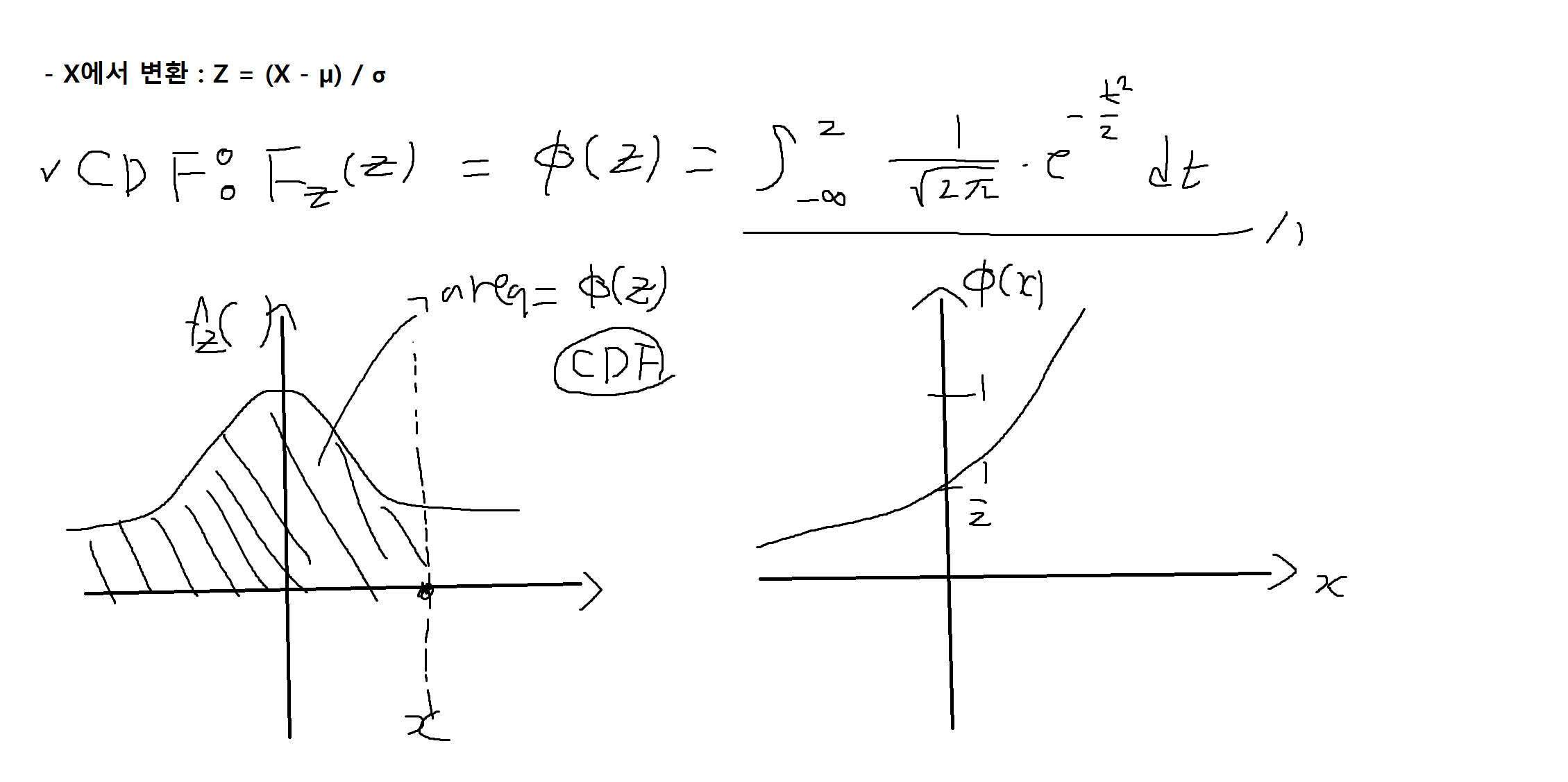
결합 가우스 확률변수(Jointly Gaussian random variables)
-
X ~ N (µx, σx²), Y ~ N(µy, σy²)가 각각 가우스 확률변수
-
ρx,y : 두 확률변수의 상관계수
-
(X, Y)의 결합확률밀도함수 (joint PDF)
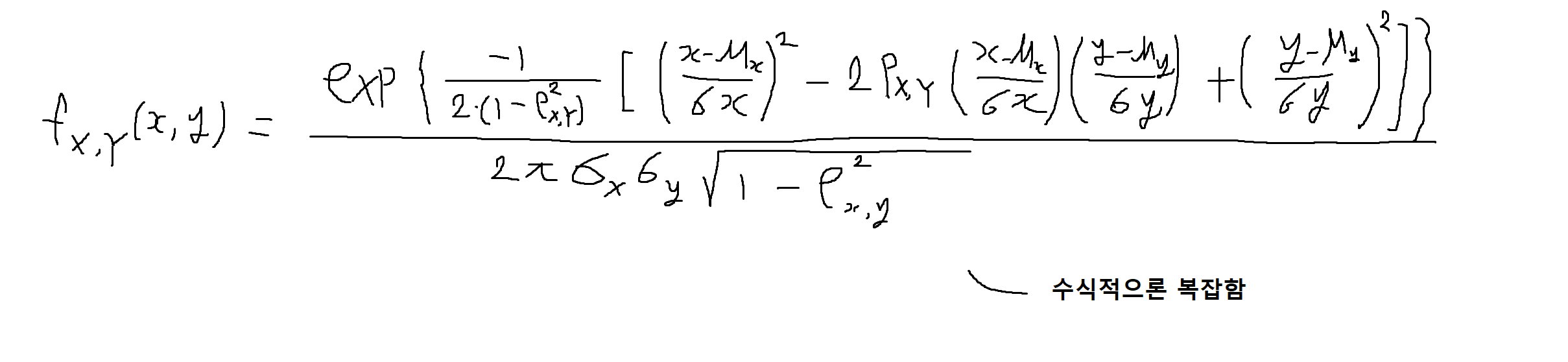
결합 가우스 확률밀도함수 그래프 1
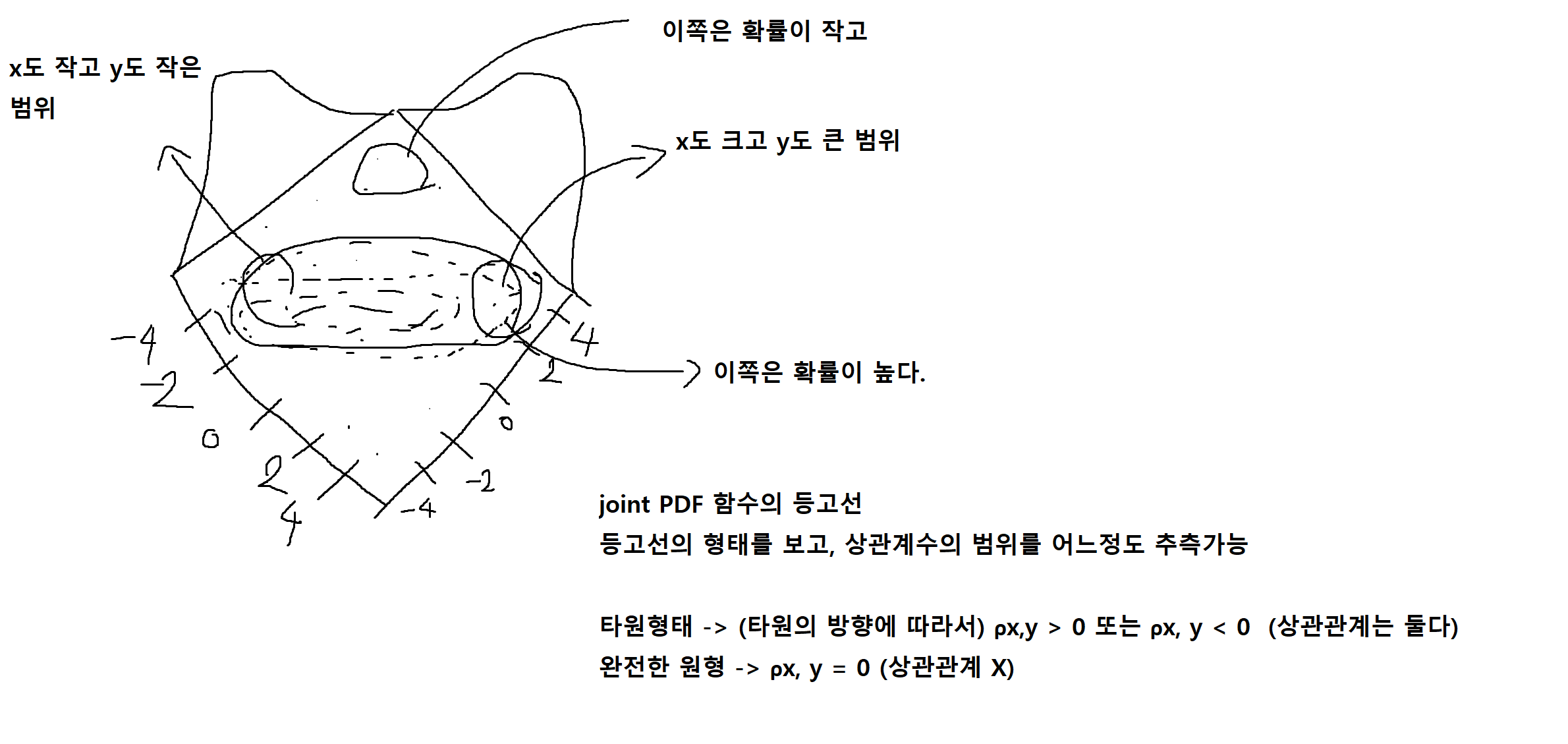
결합 가우스 확률밀도함수 그래프 2
-
Joint PDF의 등고선의 장축 (major axis)이 x축과 이루는 각도 (θ)
-
θ값의 범위에 따라 σ₁(X의 표준편차), σ₂(Y의 표준편차)의 대소관계 비교가능
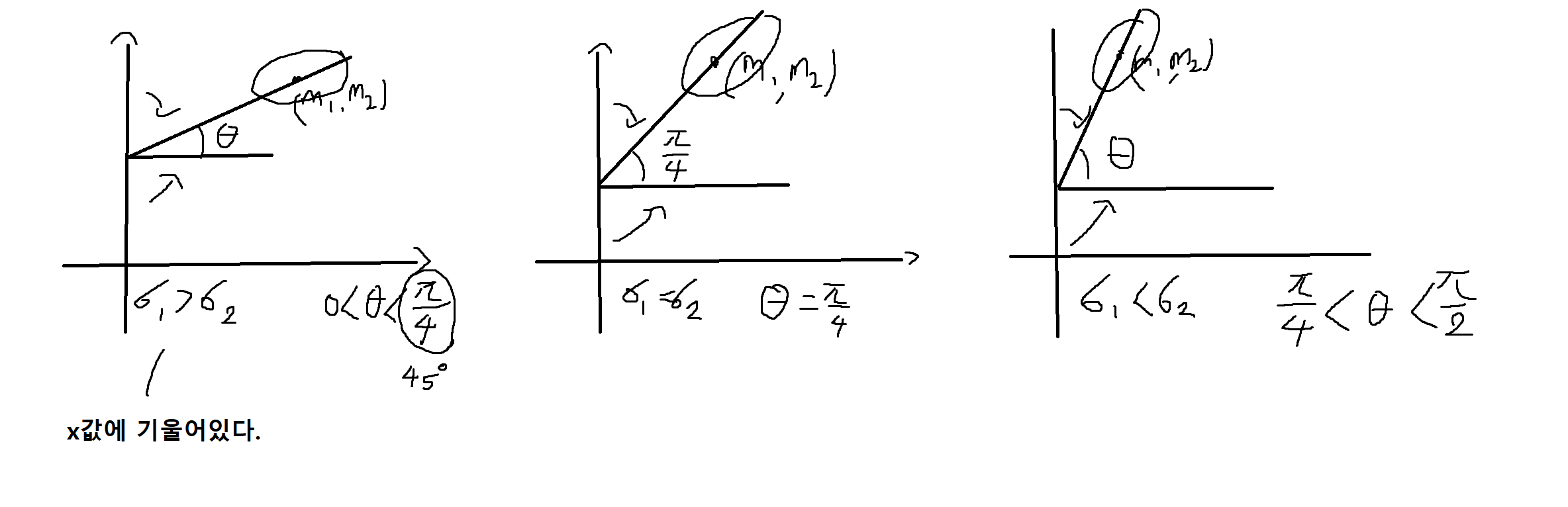
예제 5-19 : 두 확률변수 X ~ N(µx, σ²x), Y ~ N(µy, σ²y)는 각각 가우스 확률변수이다. X, Y는 독립일 때, (X, Y)의 결합확률밀도함수(Joint PDF)를 구하여라.
독립
fx,y(x,y) = fx(x) * fy(y)
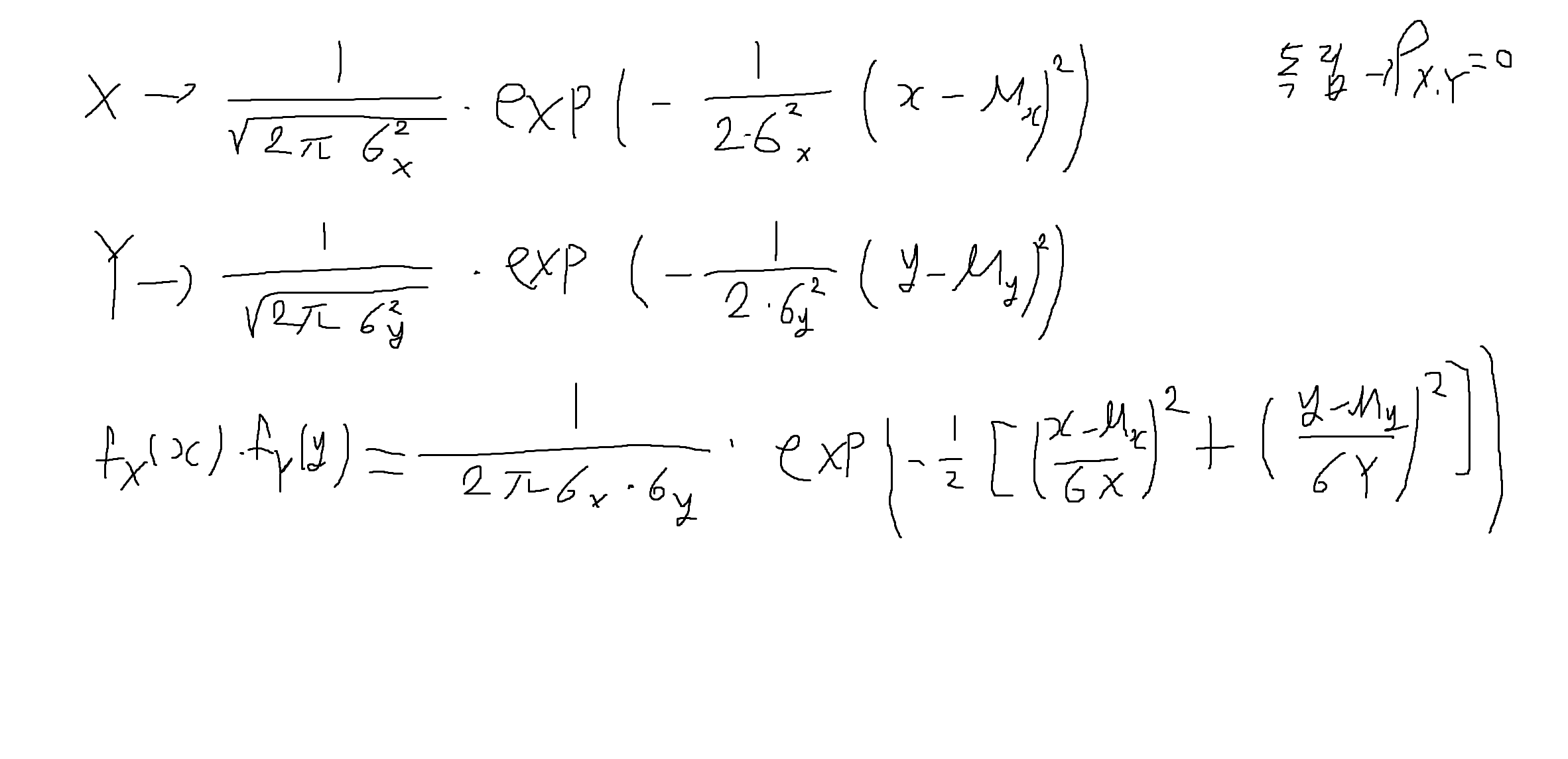
예제 5-20 : (잡음에서의 신호추정) 확률변수 X와 W은 어떤 통신시스템의 송신신호와 수신잡음을 나타내는 서로 독립인 가우스 확률변수이다. 즉, X~N (0, σ²x), W~N (0, σ²w)이다. 이 통신 시스템의 수신신호 Y = X + W 일때, Y의 평균, 분산, (X, Y)의 공분산을 구하시오.

요약
1. 두 확률변수의 결합 모멘트
-
두 확률변수 X, Y을 연관성을 파악하기 위한 척도
-
공분산, 상관관계의 정의와 의미
- 결합 가우스 확률변수
-
결정요소 : 두 확률변수의 각 평균, 분산 및 상관계수
-
그래프의 형태
