확률 및 통계 (9)

확률변수의 쌍

두 확률변수의 독립

• (복습) 확률사건의 독립

• 두 사건 A, B는 서로의 발생활률에 영향을 미치지 않음
  P[A] = P[A|B] <=> P[A∩B] = P[A] * P[B]

• 두 확률변수 (X, Y)의 독립?
  -> P[X = a] * P[Y = b] = P[X = a, Y = b]

이산확률변수일 때를 우선 생각해보자

• X = x인 경우와 Y = y인 경우의 발생확률이 서로 영향을 미치지 않음
  P[X = x, Y = y] = P[X = x] P[Y = y] <=> Px,y(x,y) = Px(x) ** Py(y)
  (joint PMF = X의 PMF Y의 PMF)

---

두 확률변수 (X, Y)의 독립

• X <= x인 경우와 Y <= y인 경우의 발생확률

• 또는 X = x인 경우와 Y = y인 경우의 확률밀도
  Fx,y(x,y) = Fx(x) * Fy(y) 또는 fx,y(x,y) = fx(x) fy(y)

P[X <= x, Y <= y] = P[X <= x] * P[Y <= y]

---

• 지금까지
  (일반적으로) 불가능(X) : 한계확률질량함수(marginal PMF) -> 결합확률질량함수 (joint PMF)
  (일반적으로) 불가능(X) : 한계누적분포함수 (marginal CDF) -> 결합누적분포함수(joint CDF)
  (일반적으로) 불가능(X) : 한계확률밀도함수 (marginal PDF) -> 결합확률밀도함수 (joint PDF)
  -> (특수한 경우로) 두 확률변수가 "독립"인 경우에는 가능

---

예제 5-11 : 확률변의 쌍 (X, Y)의 결합확률질량함수(joint PMF)가 다음과 같을 떄 X, Y의 독립여부를 판단하여라

X/Y	0	1	2
0	1/6	0	1/6
1	0	1/3	0
2	1/6	0	1/6

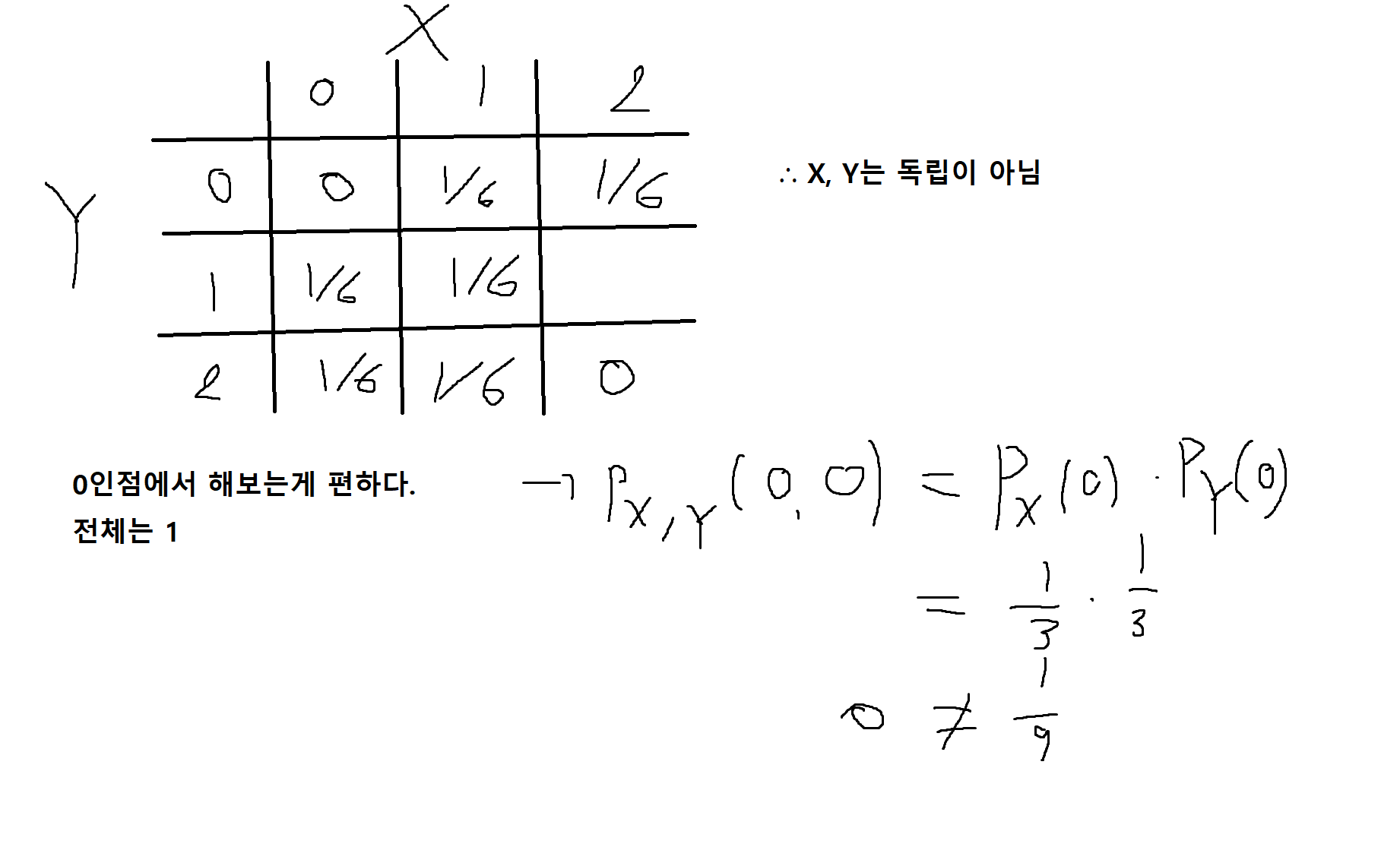
-> 9개 확인
Px,y( , ) = Px() * Py()

Px,y(0, 0) = 1/6
= Px(0) Py(0) = 1/3 * 1/3 = 1/9
1/6 != 1/9 (독립 X)

• 참고 - 0이 있으면 독립이 아닐 확률이 높음

---

예제 5-12 : (X, Y)의 결합확률밀도함수가 다음과 같을 때, X, Y의 독립여부를 판단해라 (단, α > 0, B > 0)

---

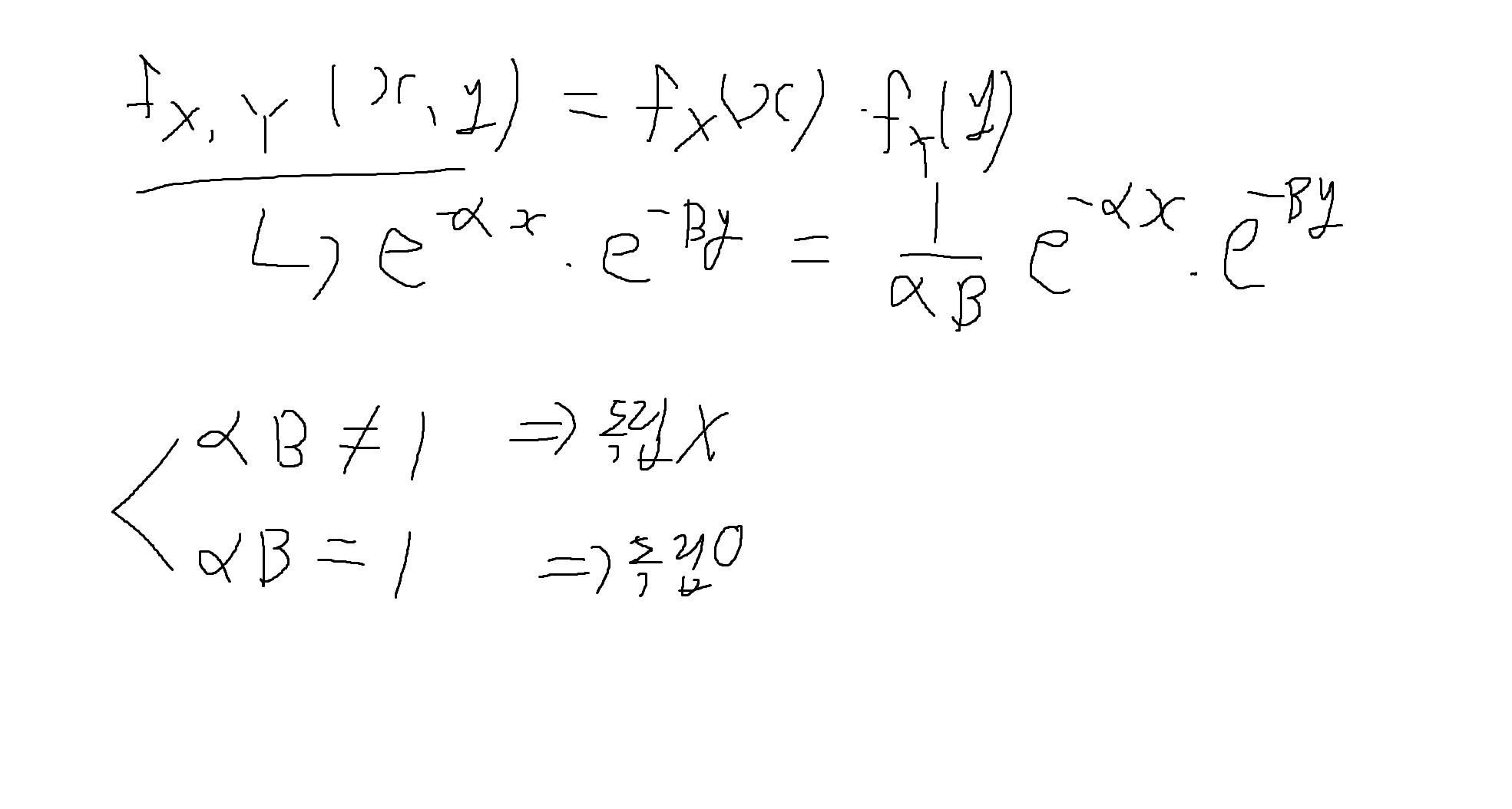
예제 5-13 : 아래의 fx,y(x, y)가 결합확률밀도함수일때, X, Y의 독립여부를 판단하여라. (*Hint : 적분구간 주의!)

예제 5-14 : 공정한 주사위를 한번 던짐으로 관찰된 점들의 수를 3으로 나누었을 때, X는 몫이고 Y는 나머지일때, X, Y의 독립여부를 판단하여라

요약

1. joint CDF와 marginal CDF의 의미

• marginal CDF를 구하는 방법 : Fx,y(x, ∞) = Fx(x)
  -> y에 ∞를 넣는다. 반대도 마찬가지

2. joint PDF와 marginal PDF의 의미

• marginal PDF를 구하는 방법 : ∫-∞ to ∞ fx,y(x,y) dy = fx(x)
  -> 적분해준다. (적분범위에 주의)

3. 두 확률변수의 독립조건

• Fx,y(x, y) -> Fx(x) Fy(y) 또는 fx,y(x,y) = fx(x) fy(y)