TF 문제
(1) (A∪B) ∩ (B-A)^c = A이다.
= (A∪B) ∩ (B∩A^c)^c
= (A∪B) ∩ (A∪B^c)
= A ∪ (B∩B^c) = A
-> T
(2) 확률실험에서 같은 절차로 구성된 실험은 항상 같은 표본공간을 가진다.
-> 주사위 2번 던질 떄 다른 값이 나옴
-> F
(3) 표본공간을 구성하는 결과의 수가 무수히 많으면 연속표본공간이다.
-> F
반례 - 동전 앞면이 나올 때까지 던진 경우
(4) 연속표본공간 S = {x|0<=x<=1, x∈R}에 대해, 사건 A = {x|x²-x=0}을 생각해볼 때, P[A] = 0이다.
-> T
-> S의 조건에 해당하는 결과들은 무한대로 많다.
-> 하나의 결과가 발생할 확률은 0임.
사건의 독립
- 독립 -> 사건 B의 발생에 대한 정보가 사건 A의 확률을 바꾸지 않는다면 두 사건 A와 B는 독립
P[A] = P[A|B] = P[A∩B] / P[B] <-> P[A∩B] = P[A] * P[B]
예제 2-15. 0과 1사이에서 임의로 두 수 x와 y를 뽑는 실험에서 사건 A = {x > 0.5}, B = {y > 0.5}, C = {x > y}을 생각했을 때, A와 B 그리고 A와 C가 각각 서로 독립임을 보여라.

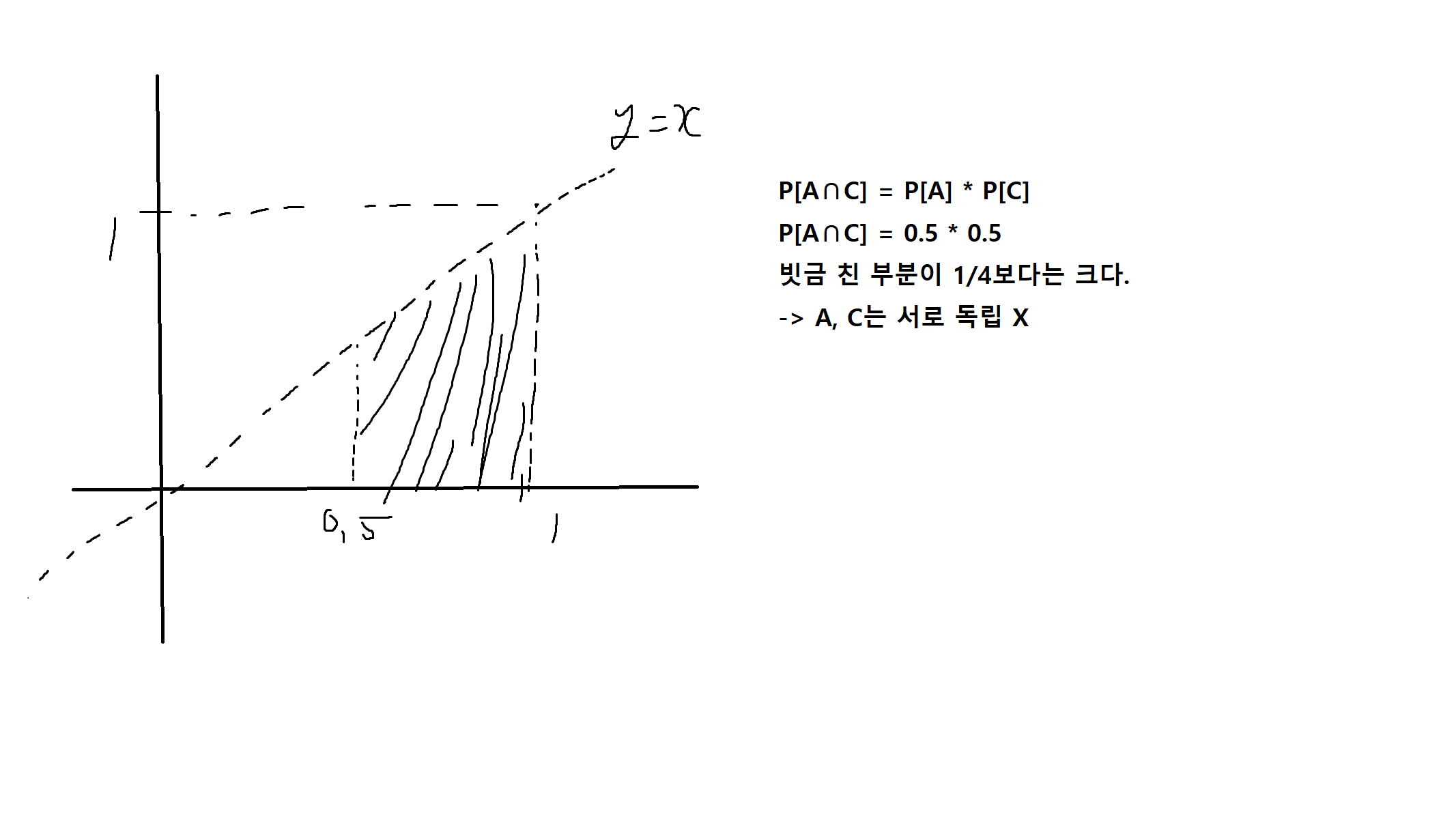
순차실험
-> 복잡한 확률실험은 단순한 하위 실험의 연속
- 독립실험의 연수 : 각 하위 실험의 결과가 다른 실험에 영향을 안 미친다.
P[A₁∩ A₂∩...∩An] = P[A₁] * P[A₂]... P[An]
각각이 독립이면
P[A₁∩ A₂∩ A₃]
= P[A₁] P[A₂] P[A₃]
예)
P[HHH] = 1/8 -> P[H] P[H] P[H] (1/2 1/2 1/2)
베르누이 실행
-> 확률 실험에서 관심있는 특정사건 A의 발생여부를 성공 또는 실패의 2가지 경우로 구분
예 2-16. (확률실험) 주사위를 1번 던진 후 윗면의 숫자를 관측, (사건 A)의 윗면의 숫자가 3 또는 5인 경우
{3, 5} -> 성공
나머지 -> 실패
예 2-17. n번의 주사위 던지기에서 특정 면이 k번 나올 확률 <-> n번의 베르누이 시행 중 k번 성공 (이항확률법칙)
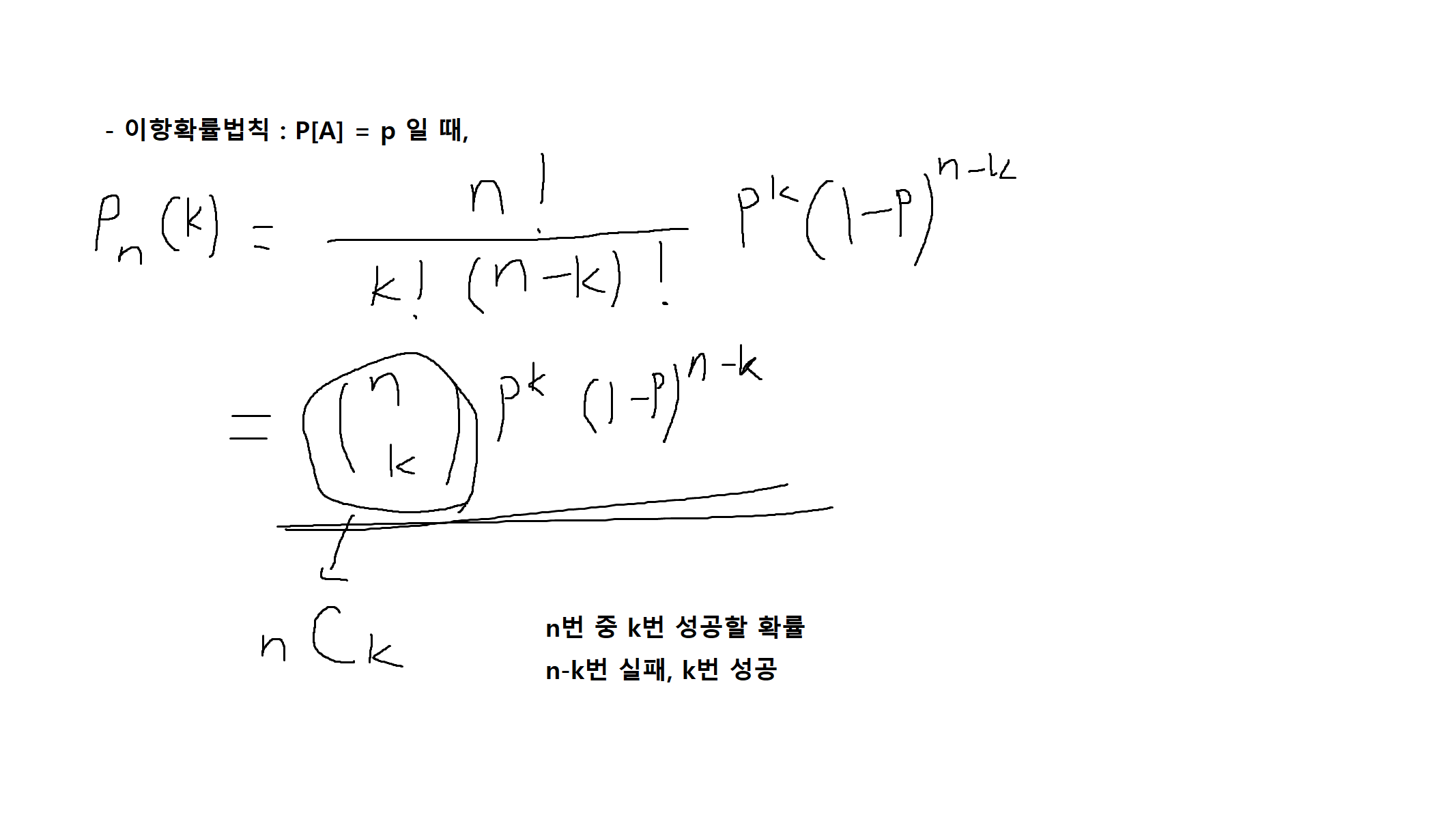
예) 3번 시행, 나올 수 있는 숫자 0, 1, 2, 3
P₃(0) + P₃(1) + P₃(2) + P₃(3) = 1
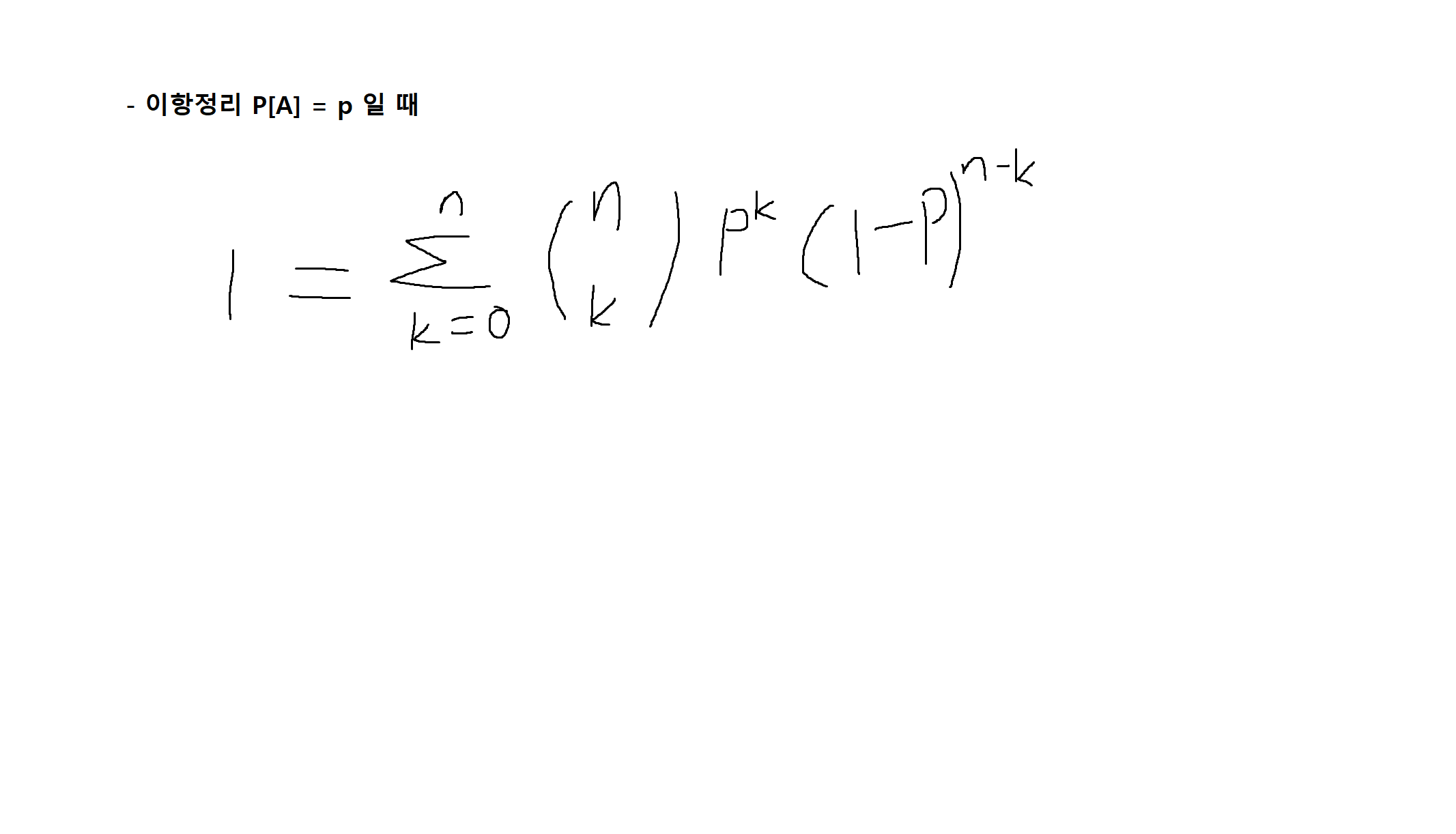
예제 2-18. 서로 대화하지 않고 독립적으로 혼자 말하는 8명의 화자 집단에서 말하는 화자의 수를 k라고 하자. 한 화자가 1/3의 확률로 말한다고 가정할 때, 말하는 화자의 수가 6보다 클 확률을 구하여라.
6보다 클 확률 -> 7일 때 확률 + 8일 때 확률
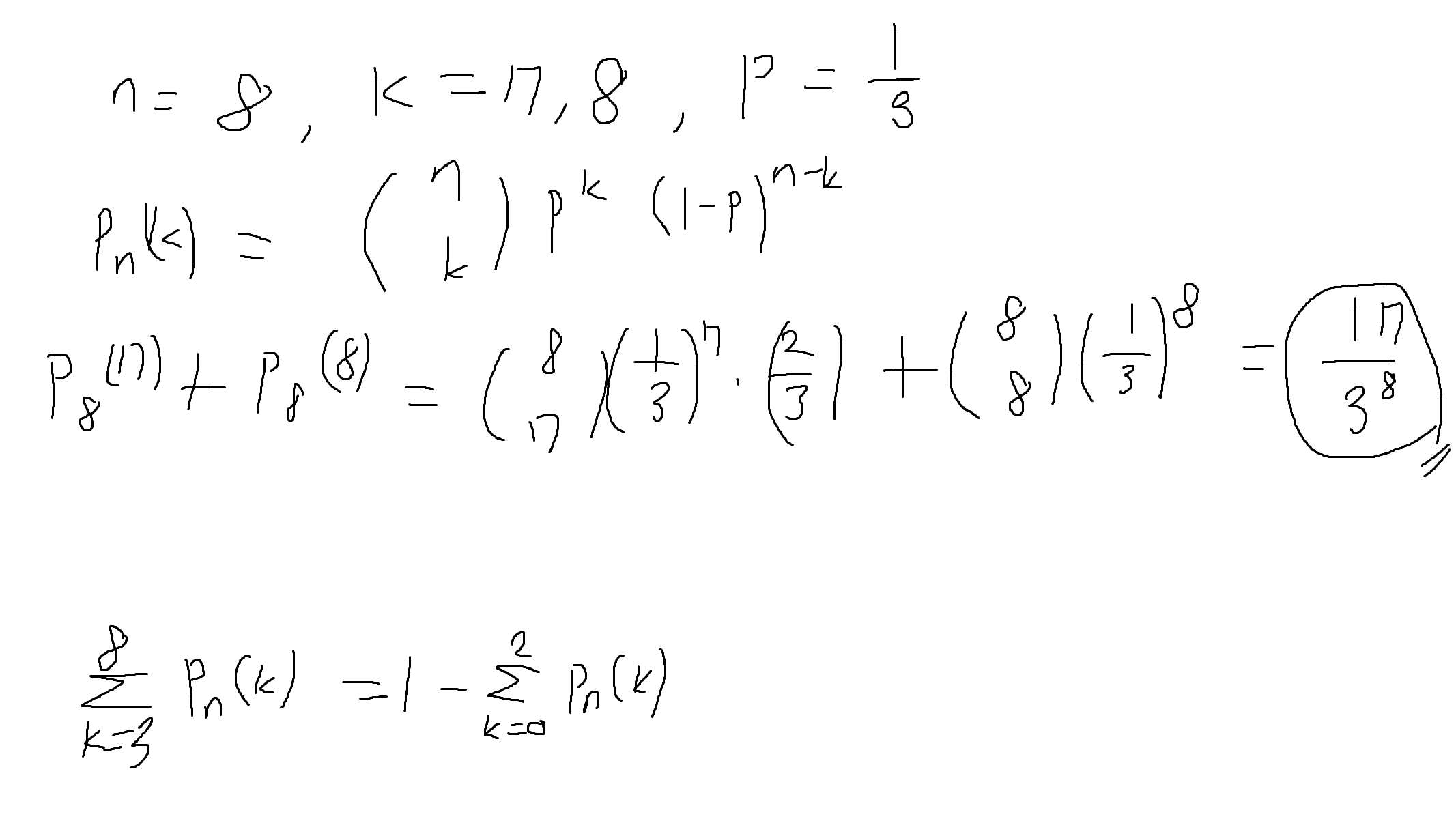
복잡한 확률실험을 단순한 하위실험의 연속
- 종속실험의 연속 : i번 째 하위실험 결과는 1 ~ i-1 번째 하위실험 결과에 영향을 받는다.
P[A₁∩ A₂∩ ... ∩ An] = P[A₁] P[A₂| A₁] ... P[An|A₁∩ A₂∩...∩An-1]
P[A₁∩ A₂] = P[A₁] * P[A₂| A₁]
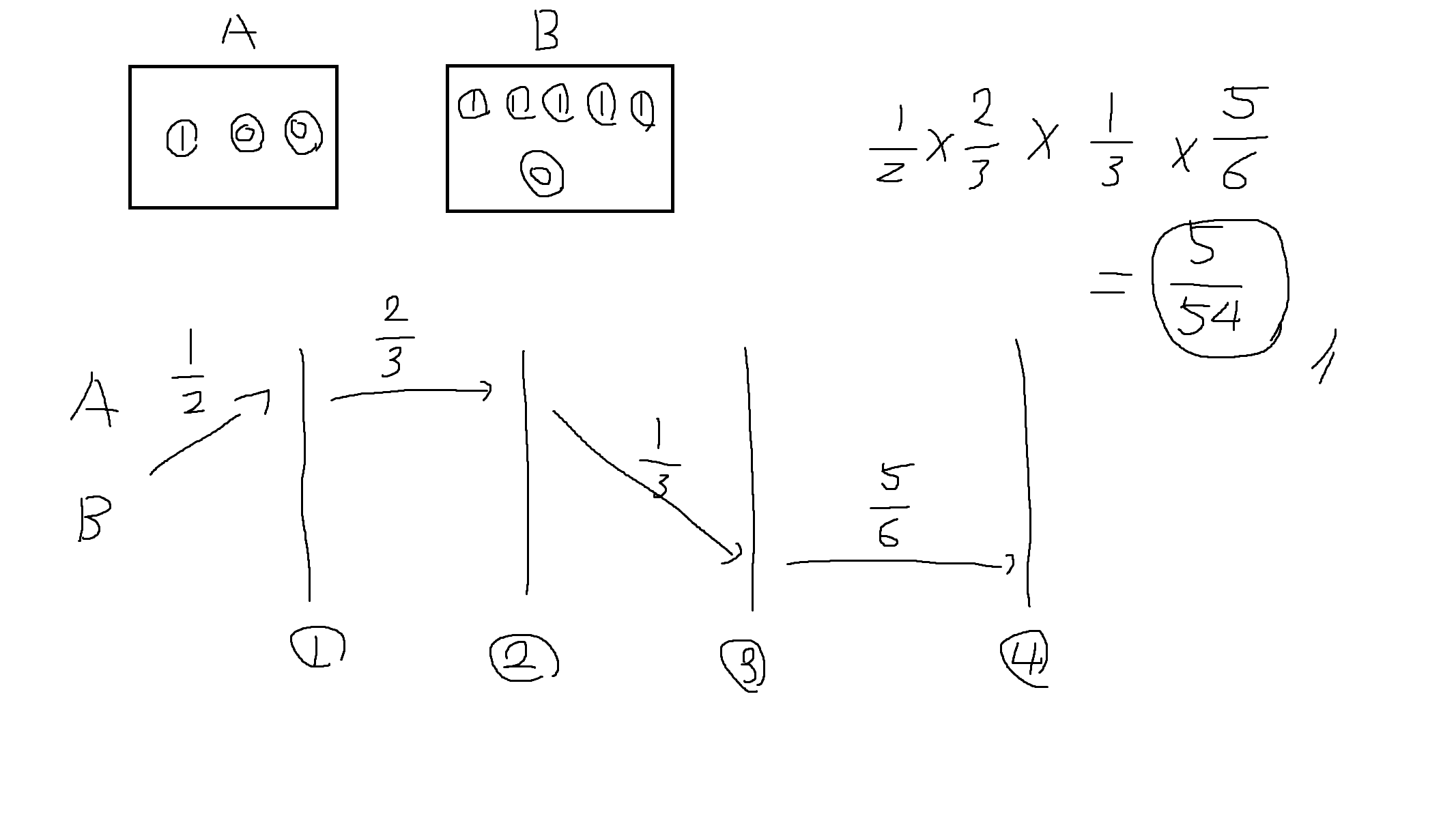
예제 2-19. A, B로 표시된 두 항아리 중 한 항아리에서 공 하나를 꺼내 그 공의 번호를 기록한 후, 원래 항아리에 다시 집어넣는 하위 실험으로 구성된 연속실험이 있다. A 항아리에는 1번공 1개 / 0번공 2개가 들어있고, B 항아리에는 1번공 5개 / 0번공 1개가 들어있다.
1) 처음에는 1/2확률의 동전던지기로 A/B 항아리 선택
2) 두번 째 시행부터는 결과에 표시된 공이 0번이면 A 항아리를, 1번이면 B항아리를 선택
3) 반복시행
Q. 이 실험에서 4번 시행 후 선택한 항아리의 순서가 AABB가 되는 확률을 구해라
확률변수의 개념
-> 확률실험의 표본공간(S) 안에 있는 결과(k)를 실수 값으로 할당하는 함수
동전던지기 (H -> 1, T -> 0)
앞면과 뒷면을 1과 0에 할당
Sx = {0, 1}
예제 3-1. 확률변수의 예
'동전을 3번 던져서 나온 앞면과 뒷면의 순서를 기록'하는 확률실험에서,
확률변수 X : 동전을 3번 던져서 나온 앞면의 수
확률변수 Y (배팅게임) : '앞면이 2번/3번 나오면 각각 $2/$8의 상금, 나머지는 $0을 받을 때, 상금의 금액'
S = {HHH, HHT, ..., TTT} -> 8가지
Sx = {0, 1, 2, 3} -> 할당
Sy = {2, 8, 0}
- 하나의 표본공간에서 다양한 확률변수를 숫자로 할당할 수 있다.
동등한 사건
P[X = x∈B] = P[A] 또는, A = {k|X(k) ∈ B}
P[B] -> X=x
예제 3-2. 예제 3-1에서 P[X=2]와 P[Y=8]을 구하여라
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
P[X=2] = 앞면이 두번 나올 확률 = (HHT, HTH, THH) -> 3/8
P[Y=8] = 상금이 $8일 확률 (앞면이 3번) (HHH) = 1/8
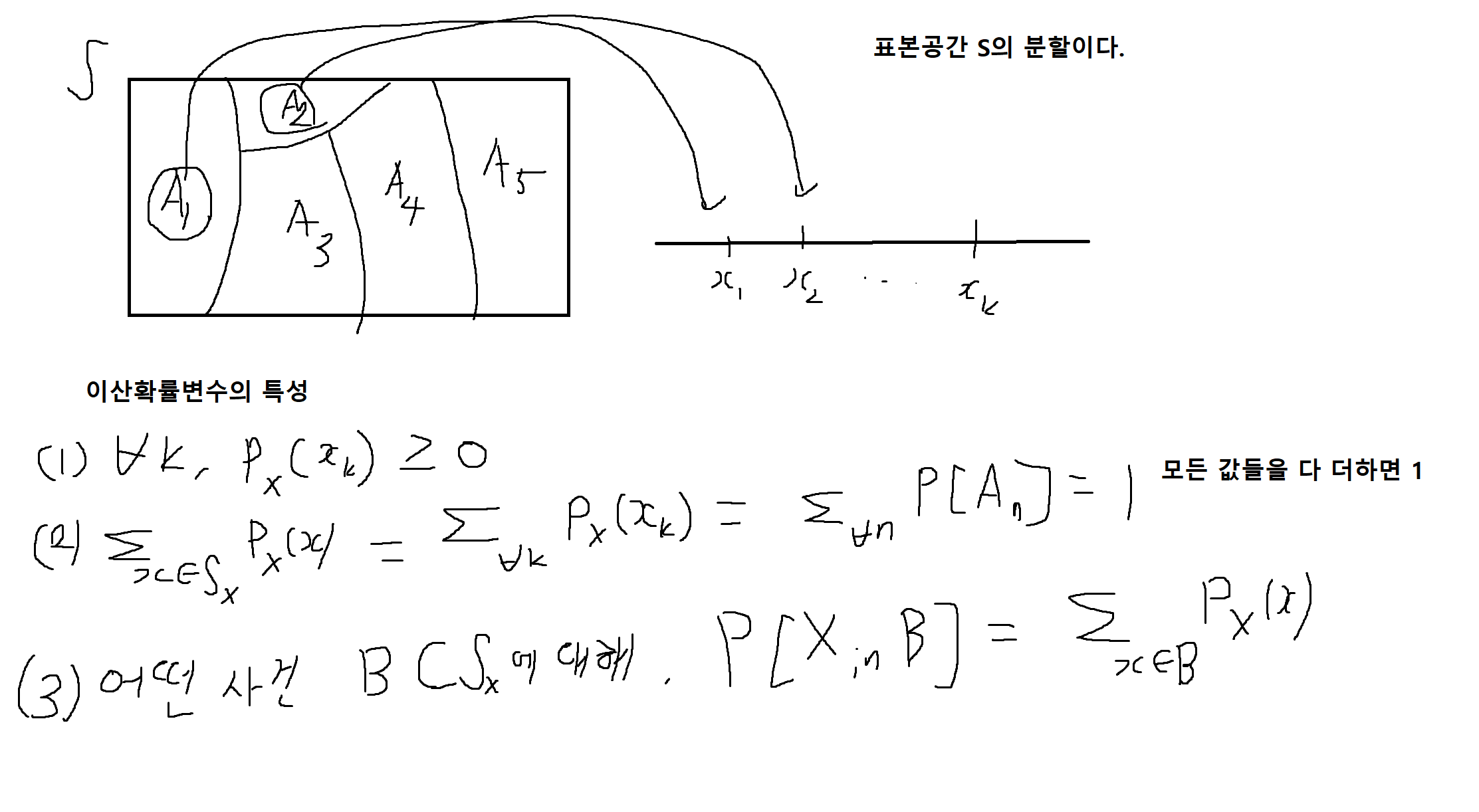
이산확률변수 : 확률변수 X의 치역 (Sx)가 불연속일 경우, X는 이산확률변수
-
우리의 주요 관심은 '확률변수 X가 특정값일 때 확률',
즉 P[X=x] (관심있는 확률의 분포를 알 수 있다는 것) -
원래 확률실험에서 X=x를 만족시키는 표본공간(S)상의 사건 ({k₁,k₂...})의 발생확률
P[X = x] = P[{k | X(k) = x}] -
확률변수 X의 특성 : 확률변수 X가 가질 수 있는 값. 그 확률의 분포 -> 확률분포
-
이산확률변수에서는 확률질량함수(PMF)를 이용
확률질량함수 (PMF) : 이산확률변수 X의 치역 Sx = {x₁, x₂... xn}에서 각 원소 값을 확률값에 대응시키는 함수
Px(x) = P[X=x]
-> 확률변수 X=x를 만족하는 표본공간 상의 사건에 대한 확률

예제 3-3. 정보소스는 세자리 이진수 {000, 111, 010, 101, 001, 110, 100, 011}를 그에 대응하는 확률 {1/4, 1/4, 1/8, 1/8, 1/16, 1/16, 1/16, 1/16}로 생성한다. 이진코드는 3자리 k에 -log₂Pk 길이의 코드워크를 할당한다. X를 정보소스의 출력에 할당된 물자열의 길이라 한다.
(1) S에서 Sx로 대하는 매핑, X의 치역을 보아라.
S = {000, 111, 010, ... , 011}
Sx = {2, 3, 4}
-> -log₂(k), k = 1/4, 1/8, 1/16
(2) X의 여러 값에 대한 확률을 구하여라
P[X=2] = 1/4 + 1/4 = 1/2 -> (000, 111) 둘중하나
P[X=3] = 1/8 + 1/8 = 1/4 -> (010, 101)
P[X=4] = 1/16 * 4 = 1/4 -> (001, 110, 100, 011)
확률변수 -> 확률실험의 S (표본공간) 안에 있는 결과(k)를 실수값으로 할당하는 함수
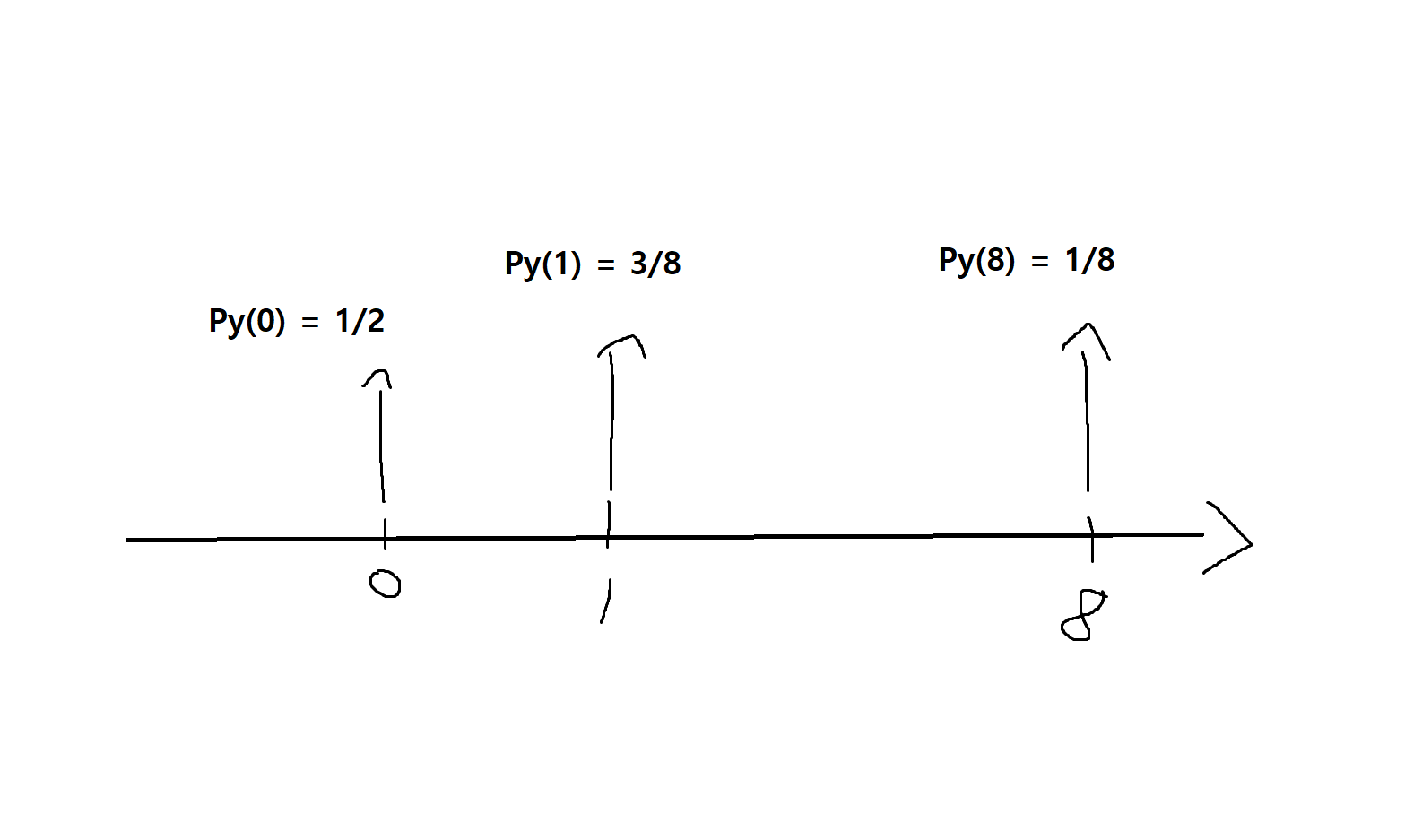
예제 3-4 : 세번의 동전던지기에서 앞면의 수가 2이면 $1을 받고, 그 수가 3이면 $8을 받지만, 그 외의 경우에는 $0를 받는 게임이 있다. 이때 이 게임의 보상을 Y라 할 때, Y의 PMF를 구해라
| P[Y=0] | P[Y=1] | P[Y=8] |
|---|---|---|
| Py(0) = 4/8 | Py(1) = 3/8 | Py(8) = 1/8 |
예제 3-5 : A를 어떤 확률실험의 관심사건이라고 할때, A의 발생여부는 베르누이 확률변수 IA가 된다. 베르누이 확률변수 IA의 PMF를 구하여라 (성공확률을 p로 가정)

예제 3-6 : X를 메시지가 목적지에 정확하게 도달할 때까지 필요한 전송횟수라 할 때, 다음을 구하시오 (단, 임의의 시행에서 메시지가 성공적으로 도달한 확률은 P이다.)
-> Sx = {1, 2, 3, 4,....}, 2 -> 1실패, 1성공 / 4 -> 3실패, 1성공

예제 3-7. 어떤 컴퓨터가 인터넷 영상 스트리밍 서비스 업체에 영상 재생을 요청할 경우 10분 동안 네트워크의 경로를 예약하고 영상을 재생할 수 있다. 영상 재생을 계속하기 위해 컴퓨터는 10분 이내에 "재생 연장" 메시지를 성공적으로 전송해야 한다. 그렇지만 이 메시지는 1/2 확률로 손실된다. 재생 연장 메시지를 보내고 승인을 받는데 10초가 걸린다고 가정하자. 99% 이상의 확률로 영상재생을 계속하기 위해 재생 연장 메시지를 보내야하는 가장 늦은 시점을 초 단위로 구하여라.

