확률변수의 함수
우리의 관심 : 확률실험의 특성파악
-
확률실험이 이미 알려진 확률변수 X로 모델링되는 경우 : CDF, PDF 그대로 이용
-
어떤 확률실험이 알려진 확률변수 X로 정확히 모델링되는 경우는 많지 않음

복습
E[X] = ∑ x * Px(x)
Y = g(x)
E[Y] = ∑ g(x) Px(x)
E[Y] = ∑ y Py(y) = ∑ g(x) * Py(y)
P[Y=y] = P[g(x) = y]
-> P[x = y^-1(y)] -> (역함수가 존재해야 가능함)
-> P[X = x] -> (Y대신 X를 써도 된다)
Y = g(x) 일때, CDF Fx(x)를 이용하여 Y의 CDF Fy(y) 표현가능!

예제 4-20: 두 상수 a != 0, b에 대해 확률변수 Y = aX + b일때, Y의 CDF와 PDF를 X의 CDF를 이용하여 구하시오.
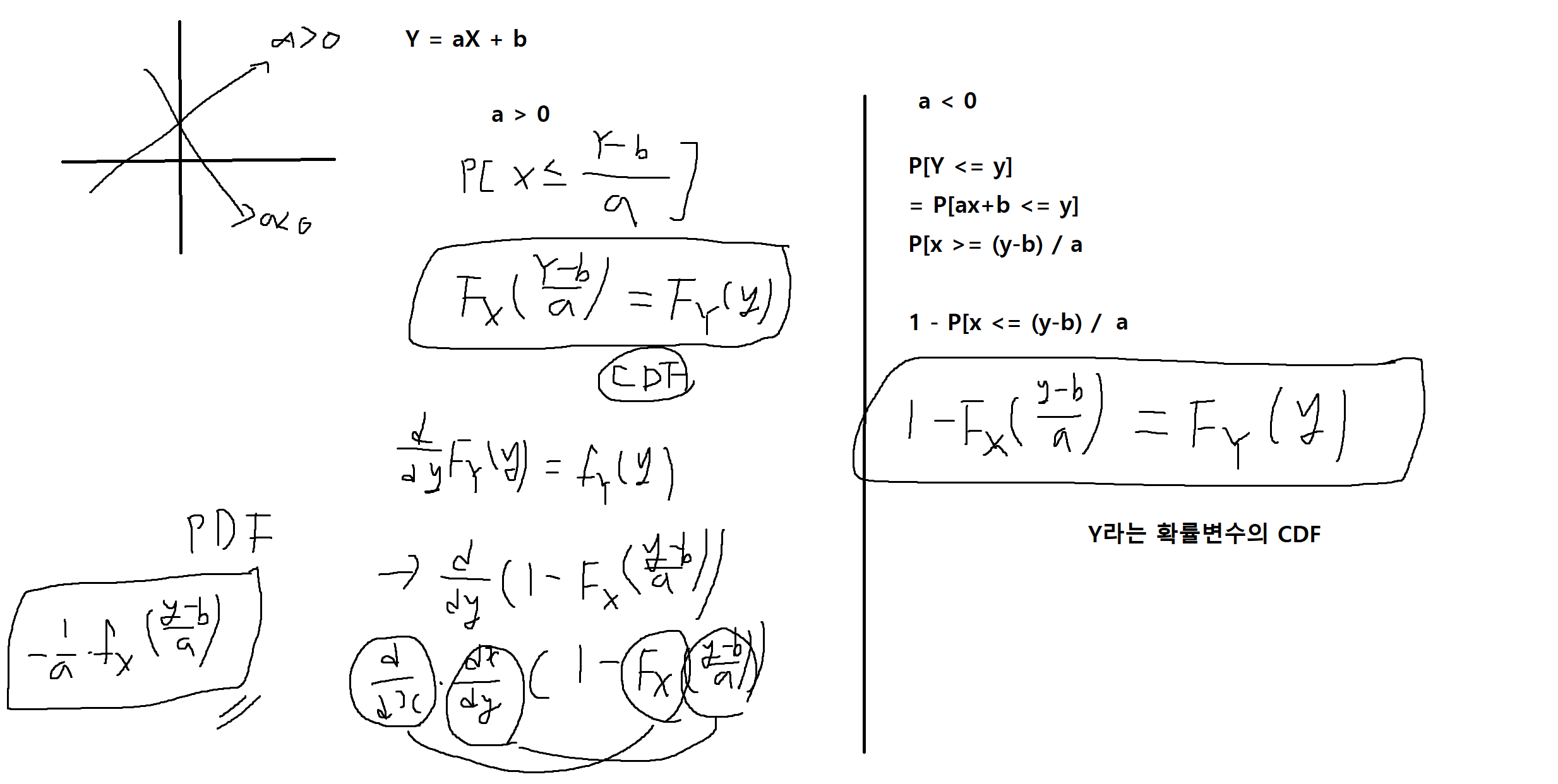
예제 4-21: 확률변수 Y = X²에 대해 Y의 CDF와 PDF를 X의 CDF를 이용하여 구하여라 (-∞ < X < +∞) -> (늘 그래프를 그려봐라)
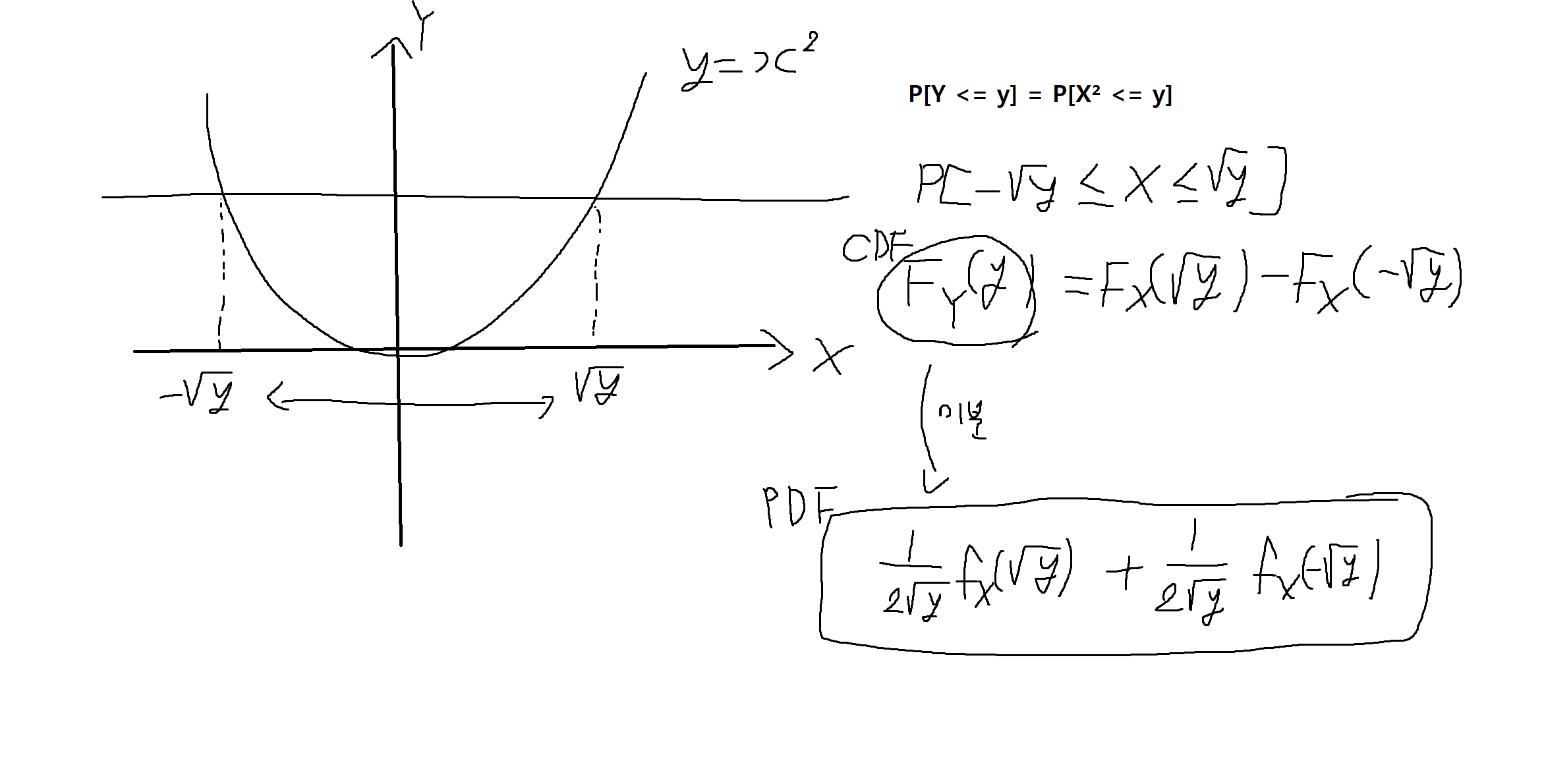
요약
- 주요 확률변수 : 균등 / 지수 / 가우스(정규)
- 표준정규분포의 변환, Φ(x)의 의미
- 확률변수의 함수
- FY(y) = P[Y <= y] = P[g(X) <= y] 의미를 이용한 변환
예제 4-22: 반경이 X인 디스크는 다음의 PDF를 가질 때, 디스크의 넓이의 PDF를 구하여라.

- T/F 확인문제
(1) 확률변수 X가 구간 [0,2]에서 정의된 균등(uniform) 확률 변수이면, Var[X] + 1 = 4/3이다.
-> T
Var[X] = (b-a)² /12 = 4 / 12 = 1/3
1/3 + 1 = 4/3
(2) 연속확률변수 X > 0가 평균이 α인 지수확률변수이면, Var[X] = α²이다.
-> F
E[X] = 1 / λ = α, λ = 1/α
Var[X] = 1 / λ² = α²
(3) fx(x)가 평균이 3인 가우스 확률변수 X의 확률밀도함수(PDF)일때, ∫-∞ to ∞ (x-3) fx(x) dx = 0이다.
-> T
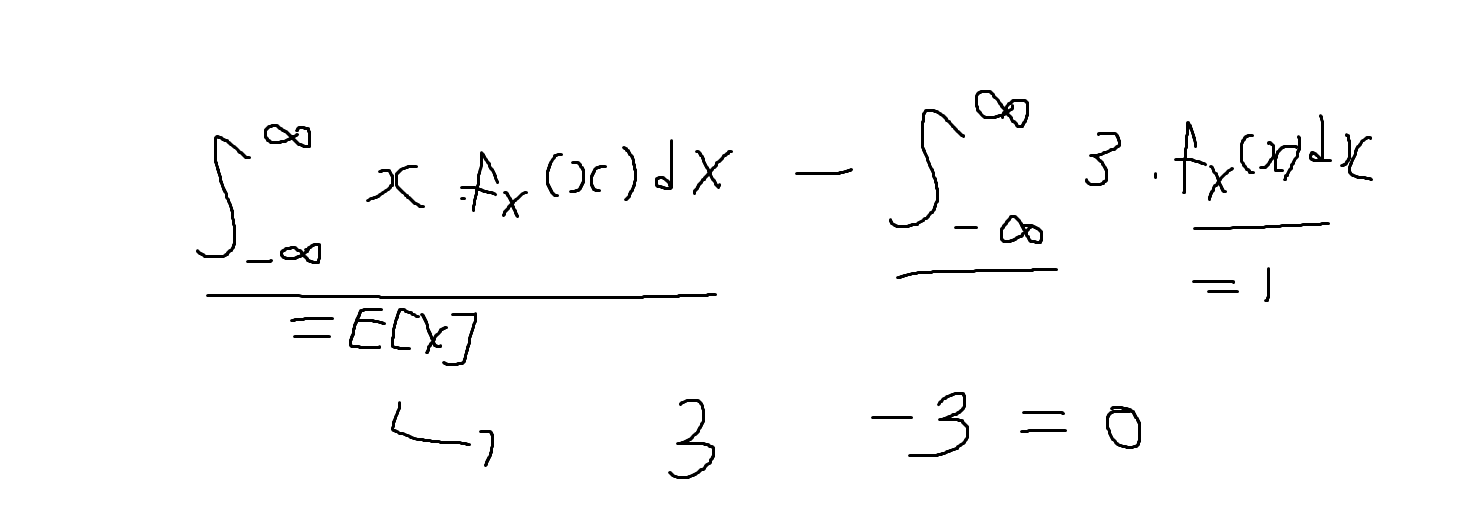
두 확률변수
- 우리의 관심 : 확률실험의 특성 파악
어떻게? 확률변수를 이용 -> 하나의 확률변수 vs 여러개의 확률변수
(잘 알려진) 이산/연속활률변수 X (학습 O)
확률변수의 함수 : Z = g(X) (학습 O)
두 확률변수 : (X,Y) (학습예정)
확률변수 Z = g(X, Y) (학습예정)
확률변수함수 (일반화) (z₁...zm) = g(X₁... Xn) (어려움 : 학습 X)
-
확률변수의 순서쌍 : (X, Y)
-
어떤 확률실험의 결과(표본공간)를 2차원 실수좌표평면(R²)에 대응
(뒤 예시 참고) -
예시 1, 실험결과: 수강생 중 학번선택 / (X, Y) = (학년, 나이)
-
예시 2, 실험결과: 동전 2번 던지기 / (X, Y) = (첫번째, 두번째)의 앞면수
-
예시 3, 실험결과: [0,1]에서 두 실수 선택 / (X, Y) = (첫번째, 두번째) 값
이산확률변수 : PMF / 확률변수 : CDF, PDF -> 어떻게 확장될 것인가?
-> 결합확률 질량함수(joint PMF), 결합 CDF, 결합 PDF
- 확률변수의 순서쌍을 포함하는 확률 계산 1
- 관심사건 A : X, Y의 관계로 표현
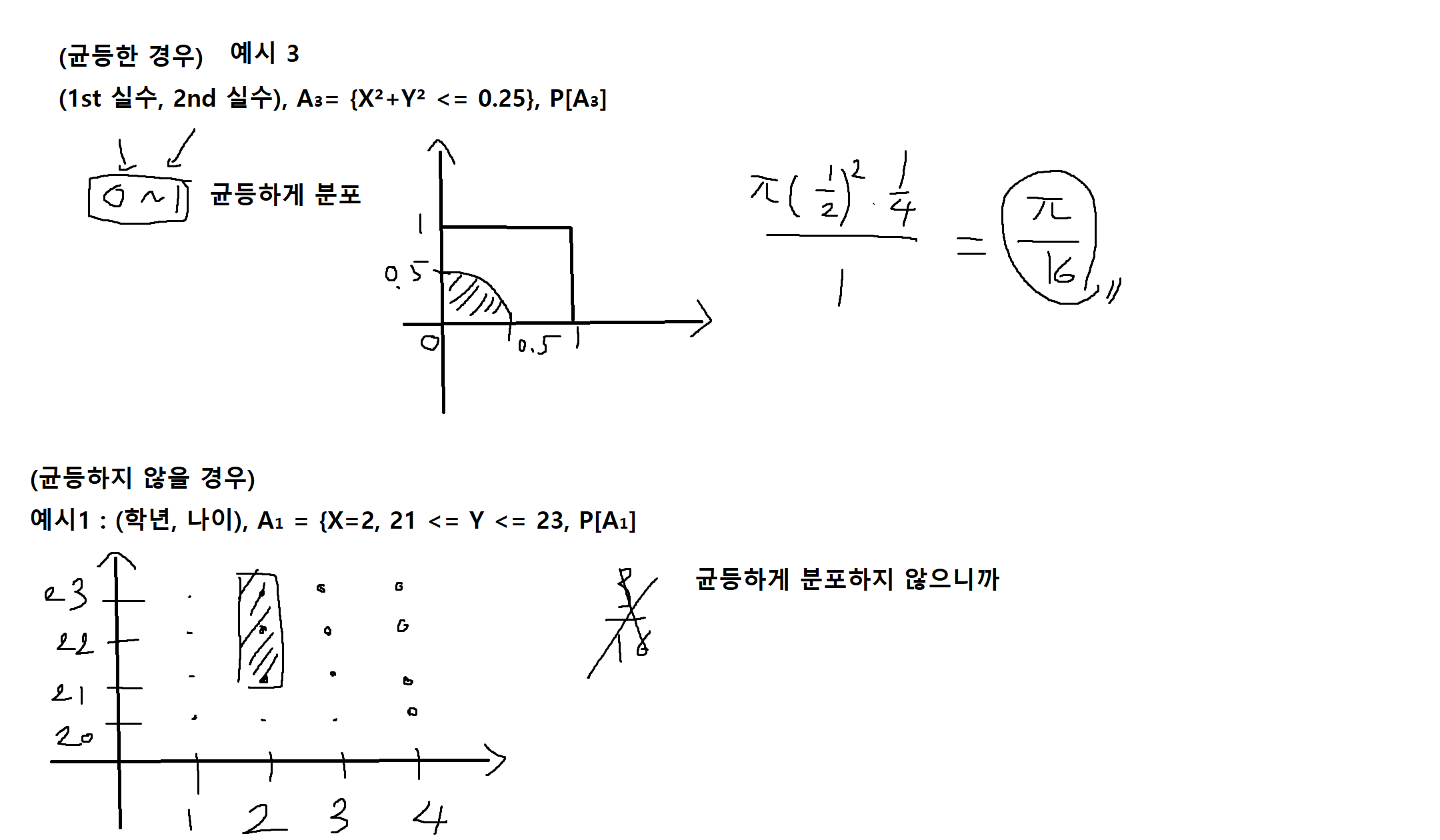
예시1 : (학년, 나이), A₁= {X = 2, 21 <= Y <= 23}
예시2 : (1st 앞면수, 2nd 앞면수), A₂= {X+Y = 1}
예시3 : (1st 실수, 2nd 실수), A₃= {X² + Y² <= 0.25}
확률변수의 순서쌍을 포함하는 확률계산 2
실수좌표평면 (R²)에서 관심영역 B : A를 만족하는 (X, Y) 순서쌍의 영역
P[A] = P[관심 (X,Y)영역] = P[B] = P[B에 대응하는 사건 ⊂ 표본공간]
P[A] != 관심영역(B) / 전체영역 -> (균등할 때만 가능함)
-> 일반적으로 성립하지 않음
(* 성립전제 조건 : (X,Y)가 R²에서 균등하게 분포)
결국, X,Y의 분포를 통합적으로 고려해야 함! -> "joint" PMF / CDF / PDF
결합확률 질량함수
-
확률변수의 순서쌍 (X, Y)에서 X, Y 모두 이산확률변수
-
하나의 이산확률변수에서 P[X=x]가 존재 -> P[X = x]
-
특정 하나의 순서쌍 ((X, Y) = (x, y))에 대한 확률이 존재
P[(X, Y) = (x, y) = P[{X=x} ∩ {Y=y}] = P[X = x, Y = y]
P[X = a] = Px(a) -> PMF
-
확률질량함수 (PMF) : Px(x) = P[X = x]
-
결합확률 질량함수 (joint PMF) : Px,y(x,y) = P[X = x, Y = y]
-
Px,y = Pxy (콤마 없이도 많이 쓴다.)
결합확률질량함수 (joint PMF)를 이용한 확률 계산
-
모든 (X,Y) 순서쌍 집합 : Sx,y = {(xn, ym) | n = 1,2,..., m=1,2...}
-
실수좌표평면 (R²)에서 관심영역 B : 관심있는 (X, Y) 순서쌍 영역

예제 5-1 : 카를로와 마이클이 앞면과 뒷면이 나올 확률이 같은 동전을 두번씩 (각각 두번씩) 던질 떄, 나온 윗면의 수의 최대값 X, 최소값 Y라고 할 때, 다음을 구하여라.
(1) 앞/뒷면을 관측하는 확률실험의 표본공간 S와 모든 (X, Y)의 집합 Sx,y을 구하여라
S = { (HH, HH), (HH, HT), (HH, TH), (HH, TT), (HT, HH), (HT, HT), (HT, TH), (HT, TT), (TH, HH), (TH, HT), (TH, TH), (TH, TT), (TT, HH), (TT, TH), (TT, TT)}
Sx,y = { (0,0), (1,0), (1,1), (2,0), (2,1), (2,2)}
-> S는 균등하고 Sx,y는 균등하지 않다.
(2) 결합확률질량함수 (joint PMF)와 P[X=Y]의 값을 구하여라
| Y/X | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 1/16 | 4/16 | 2/16 |
| 1 | 0 | 4/16 | 4/16 |
| 2 | 0 | 0 | 1/16 |
-> 다 더하면 1
P[X=Y] -> (0,0), (1,1), (2,2)
= 6/16
예제 5-2 : 3ms 동안의 웹 페이지 요청수를 X, 그 다음 3ms 동안의 웹 페이지 요청수는 Y라고 하자. 1ms 안에 웹 페이지 요청은 0.5확률로 0번 또는 1번 발생한다. 매 1ms 안에 웹 페이지 요청은 독립적으로 발생할 때, 다음을 구해라
(1) 확률실험의 표본공간 S와 모든 (X,Y)의 집합 Sx,y을 구하여라
S = {(0,0,0,0,0,0), ... , (1,1,1,1,1,1)}
Sxy = {(0,0), (0,1), ... , (3,3)}
(2) 결합확률질량함수 (joint PMF)와 P[X+Y = 2]의 값을 구하여라
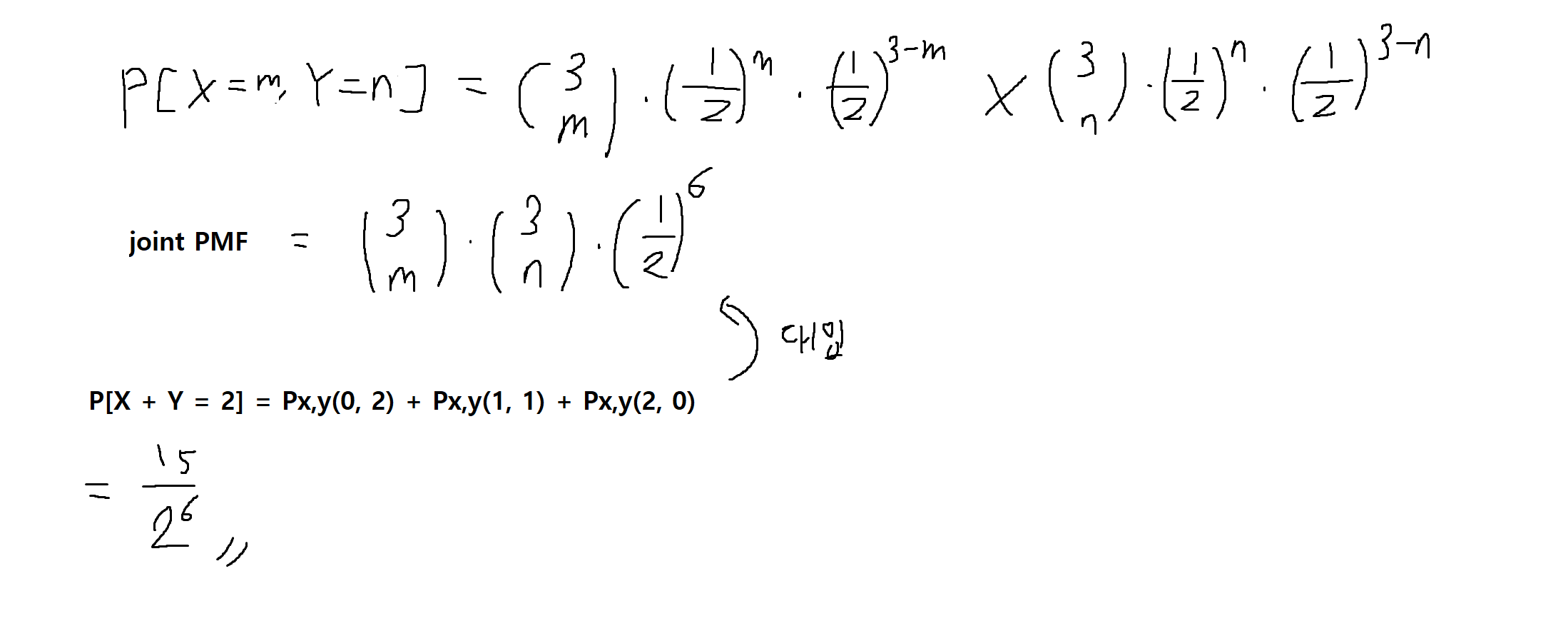
-
결합확률 질량함수 (joint PMF)는 X, Y의 결합특성에 관한 정보제공
-
예시 4 : 편중된 두개의 동전을 던져 각 동전의 앞면의 여부를 (X, Y) 기록하는 실험
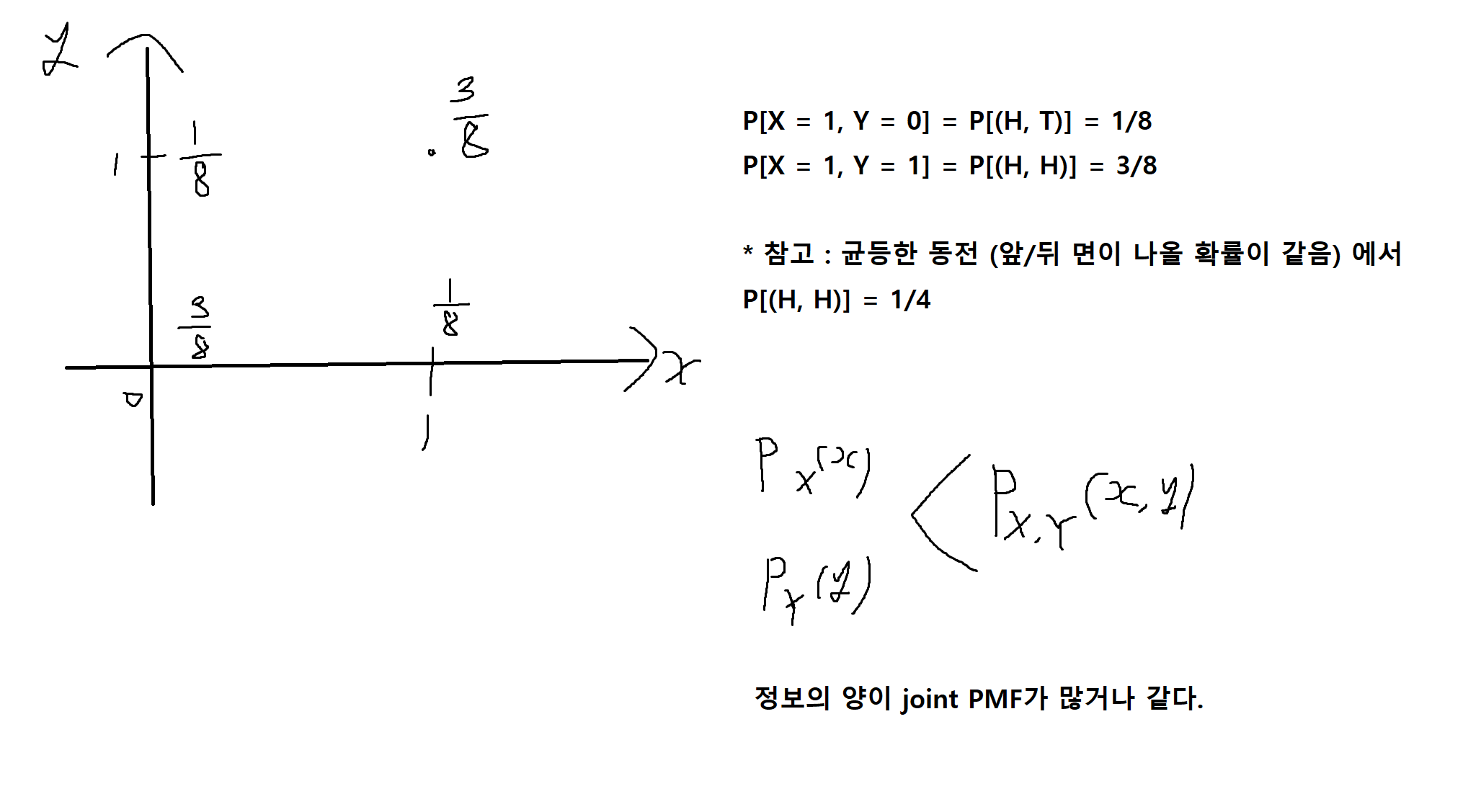
- 각 확률변수를 분리시켜 생각할 때는 어떻게? (예 : Y와 상관없이 X에 관한 사건의 확률)
P[{X = 1}] = P[{X = 1 ∩ Y = 0} ∪ {X = 1 ∩ Y = 1}] = 1 / 2
-> 1/8 + 3/8 = 1/2
-> X = 1일 때 Y가 가질 수 있는 값들의 합
P[X = 0] = 1/2
P[Y = 0] = 1/2
P[Y = 1] = 1/2
-> 각각봐서는 이상한 동전(1/8, 3/8 확률값이 다르니까 이상) 이라는 걸 알 수 없는데
-> joint PMF로 보면 이상하다는 걸 알 수 있다.
한계확률질량함수 (marginal PMF) :

Joint PMF
1) 더 많은 정보
2) marginal PMF
- (일반적으로) 가능 (O) : 결합확률질량함수(joint PMF) -> 한계확률질량함수(marginal PMF)
- (일반적으로) 불가능 (X) : 한계확률질량함수 (marginal PMF) -> 결합확률질량함수 (joint PMF)
(앞에 그래프를 보면
P[X = 1] = 1/2
P[Y = 1] = 1/2
을 안다고 1/8, 3/8 값을 알 수는 없다.
예제 5-3 : 확률변의 쌍 (X,Y)가 다음과 같은 결합확률질량함수를 갖을 때, 다음을 구하시오.
(a)
| X/Y | -1 | 0 | 1 |
|---|---|---|---|
| -1 | 1/6 | 0 | 1/6 |
| 0 | 0 | 1/3 | 0 |
| 1 | 1/6 | 0 | 1/6 |
(b)
| X/Y | -1 | 0 | 1 |
|---|---|---|---|
| -1 | 1/9 | 1/9 | 1/9 |
| 0 | 1/9 | 1/9 | 1/9 |
| 1 | 1/9 | 1/9 | 1/9 |
(1) 한계확률질량함수(marginal PMF)를 구하여라
(a)
Px(-1) = 1/6 + 0 + 1/6 = 1/3
Px(0) = 0 + 1/3 + 0 = 1/3
Px(1) = 1/6 + 0 + 1/6 = 1/3
(b)
Px(-1) = 1/9 * 3 = 1/3
Px(0) = 1/9 * 3 = 1/3
Px(1) = 1/9 * 3 = 1/3
-> a, b의 Y marginal PMF도 똑같다.
(2) 사건 A = {X <= 0}, B = {X <= Y}의 확률을 구하여라
(a)
P[A] = P[X<=0] = P[X=0] + P[X=-1] = 2/3
P[B] = 1/6 + 0 + 1/3 + 1/6 + 0 + 1/6 = 5/6
(b)
P[A] = P[X<=0] = 1/3 + 1/3 = 2/3
P[B] = 1/9 * 6 = 2/3
예제 5-4 : 동전을 2n번 던져 그 결과에 따라 로봇이 움직이는 확률실험이 있다.
-
로봇은 처음에 원점(0, 0)에 위치
-
매 짝수 번째 순간마다 동전던지기의 결과 (앞면/뒷면)에 따라 x축 방향으로 +d cm 또는 -d cm 만큼 이동
-
매 홀수 번째 순간마다 동전던지기의 결과 (앞면/뒷면)에 따라 y축 방향으로 +d cm 또는 -d cm 만큼 이동
2n번째 동전던지기 후의 로봇의 위치를 확률변수의 쌍 (X,Y)이라고 할 때, n=4이고 d=1일 때, 로봇이 원점으로부터 2^(1/2) 거리 안에 있을 확률을 구하시오
풀이
-> n=4 -> 2n = 8번 던짐. x축 / y축 (4번 / 4번) 분리해서 생각
x축 4번 중 m번 앞면 -> 4-m번 뒷면
md - (4-m)d, (d=1)
m - 4 + m
= 2m - 4
m = 0, 1, 2, 3, 4 (대입)
거리 r
r² = x² + y²
2 = x² + y²


정말 잘 읽었습니다, 고맙습니다!