확률 및 통계 (8)

확률변수의 쌍 (2)

• 복습

• 결합누적분포함수 (joint CDF)

• 결합확률밀도함수 (joint PDF)

• 두확률변수의 독립

• 요약

• PDF는 (셀수있는 경우). 특정한 지점에서의 확률 의미 있음,
  PMF는 (셀수없는 경우). 특정한 지점에서의 확률은 의미없고 구간에서의 확률이 의미가 있다.

---

• T / F 확인문제
  (1) 두 이산확률변수 X, Y 각각의 한계질량함수 (marginal PMF)를 알고 있으면 항상 순서쌍 (X, Y)의 결합확률질량함수 (joint PMF)를 구할 수 있다.
  -> F (반대가 참)

(2) Px,y(x,y)는 치역(range)이 Sx = Sy = {1,2,...,10}인 두 이산확률변수 X, Y의 결합확률밀도함수(joint PMF)이다. Px(x)와 Py(y)를 두 확률변수의 한계확률밀도함수(marginal PMF)라고 정의할 때, 다음이 성립한다.

---

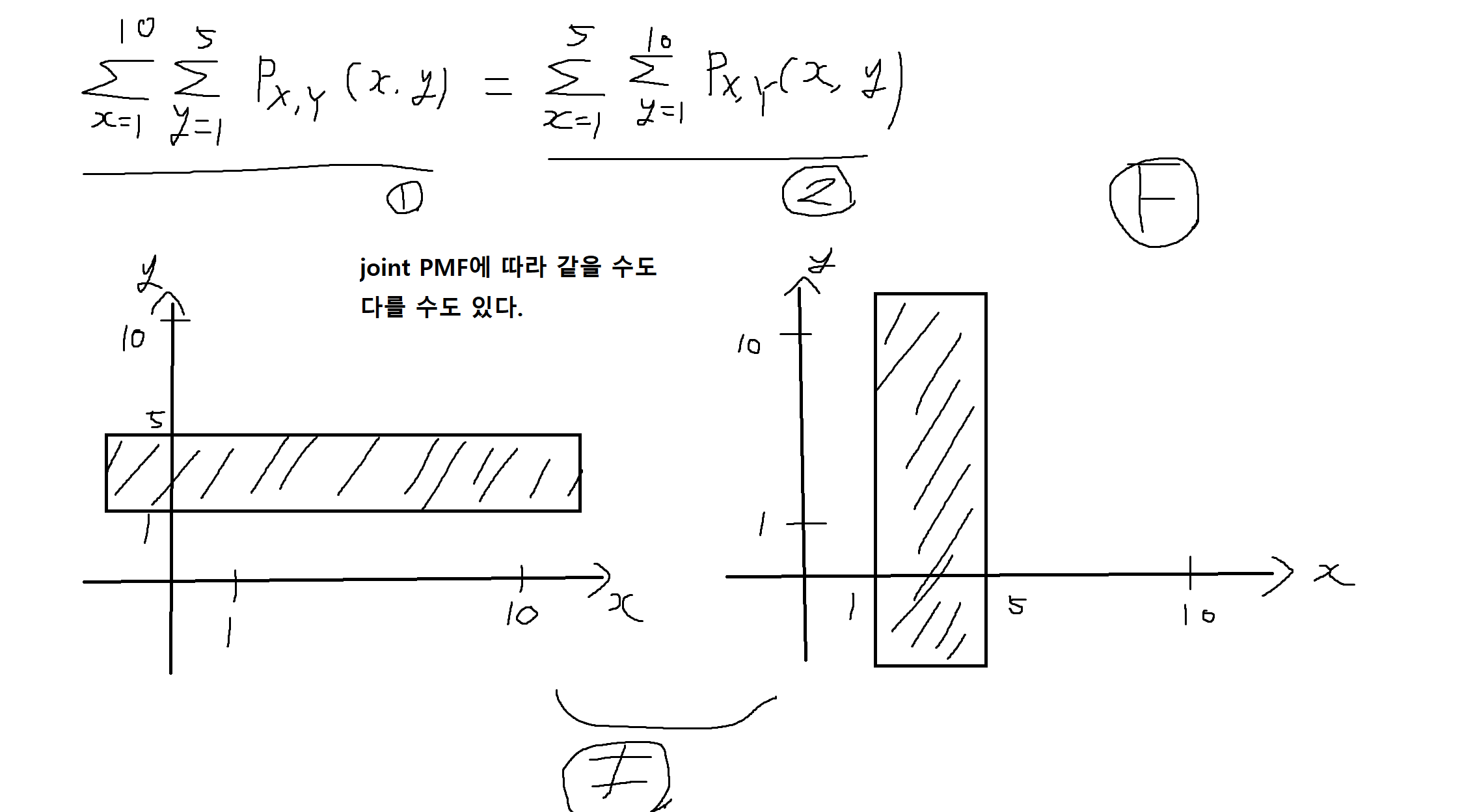
결합누적분포함수 (joint CDF)

• 확률변수의 순서쌍 (X, Y) 특성 파악하기

• 하나의 확률변수에서 P[X <= x]를 이용 (1차원) -> Fx(x) = P[X <= x]

• 순서쌍 (X, Y)가 특정 (2차원)범위에 존재할 확률을 이용 : P[X <= x, Y <=y]

누적분포함수(CDF) : Fx(x) = P[X <= x]
결합누적합수(joint CDF) : Fx,y(x, y) = P[X <= x, Y <= y]

---

• (복습) 누적분포함수(CDF)의 특성 (확률변수 X)

(1) 0 <= Fx(x) <= 1

(2) lim x to ∞ Fx(x) = 1

(3) lim x to -∞ Fx(x) = 0

(4) a < b이면 Fx(a) <= Fx(b)

(5) P[a < X <= b] = Fx(b) - Fx(a)

(6) P[X > x] = 1 - Fx(x)

---

• 결합누적분포함수(joint CDF)의 특성 : 확률변수의 순서쌍 (X, Y)
  -> P[X <= x, Y <= y]

(1) 0 <= Fx,y(x, y) <= 1

(2) x₁<= x₂ 그리고 y₁<= y₂이면 Fx,y(x1, y1) <= Fx,y(x2, y2)

(3) Fx,y(x, -∞) = 0 -> (-∞가면 공집합이 된다)
Fx,y(-∞, y) = 0
Fx,y(∞, ∞) = 1 -> P[X <= ∞, y <= ∞] = 즉 모든 영역

(중요) (4) Fx,y(x₁, y₁) - Fx,y(x₂, y₁) - Fx,y(x₁, y₂) + Fx,y(x₁ , y₁)

---

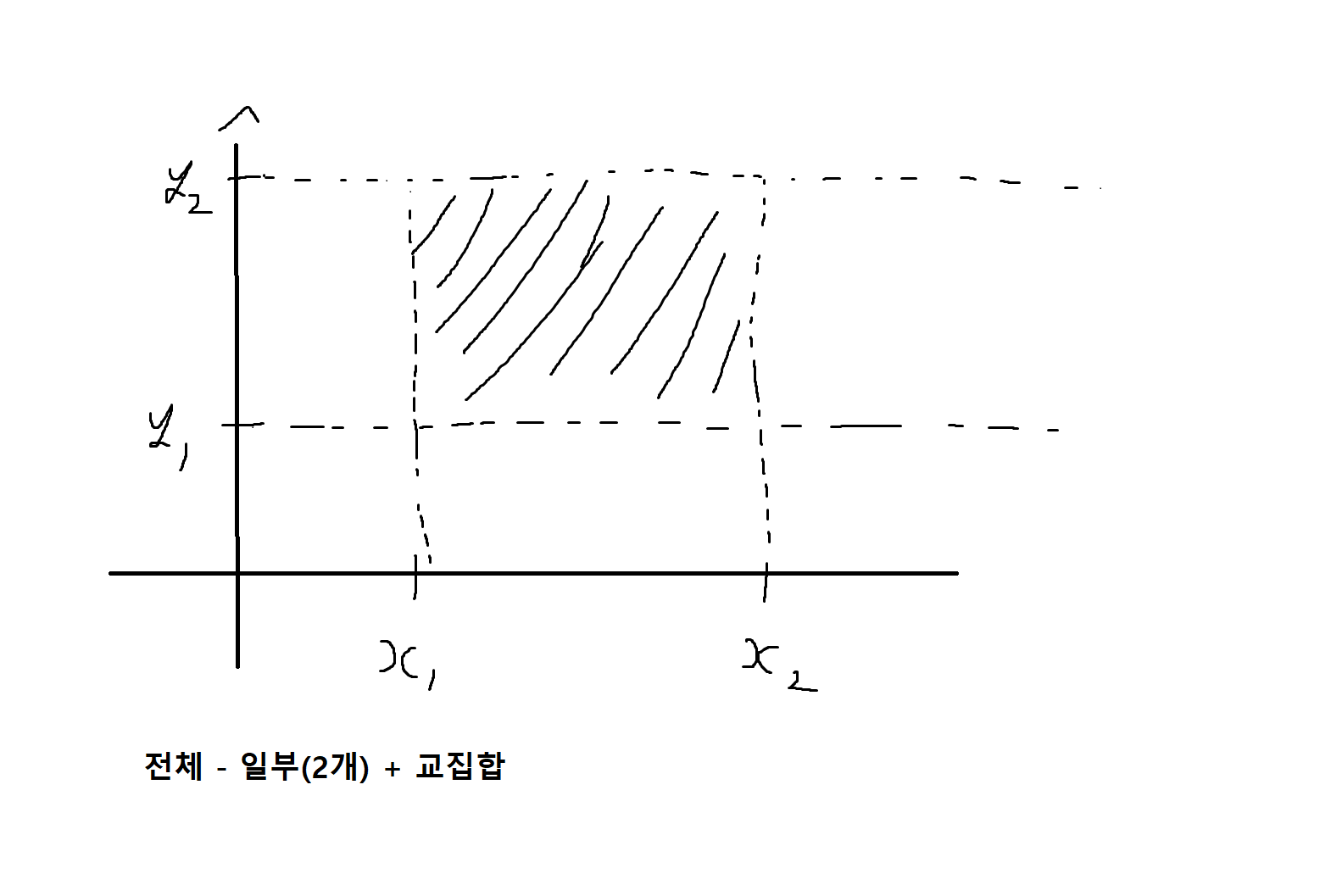
한계누적분포함수 (marginal CDF)

• 결합누적분포함수에서 제거하고자 하는 확률변수의 전체 범위를 계산
  Px(x) = Fx,y(x, ∞) = P[{X <= x} ∩ {Y < ∞}] = P[X <= x]
  -> P[Y < ∞] = 1
  Py(y) = Fx,y(∞, y) = P[{X < ∞} ∩ {Y <= y} = P[Y <= y]

• (일반적으로) 가능(O) : 결합누적분포함수(joint CDF) -> 한계누적분포함수(marginal CDF)

• (일반적으로) 불가능(X) : 한계누적분포함수(marginal CDF) -> 결합누적분포함수(joint CDF)

-> 결합이 정보가 더 많다.

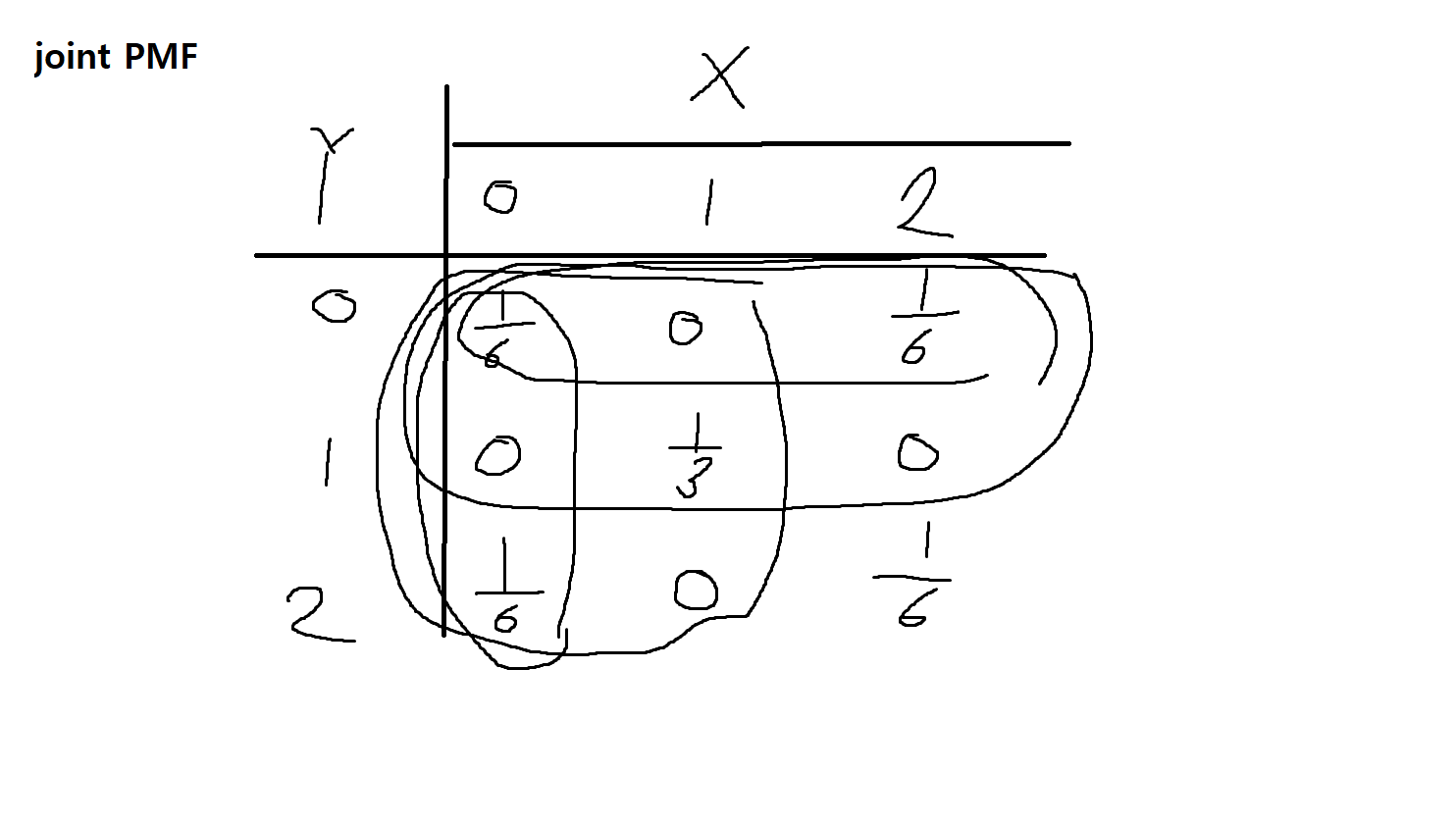
예제 5-5 : 확률 변의 쌍(X, Y)의 결합확률질량함수(joint PMF)가 다음과 같을 때, 결합누적분포함수(joint CDF)를 구하여라.

joint PMF

X/Y	0	1	2
0	1/6	0	1/6
1	0	1/3	0
2	1/6	0	1/6

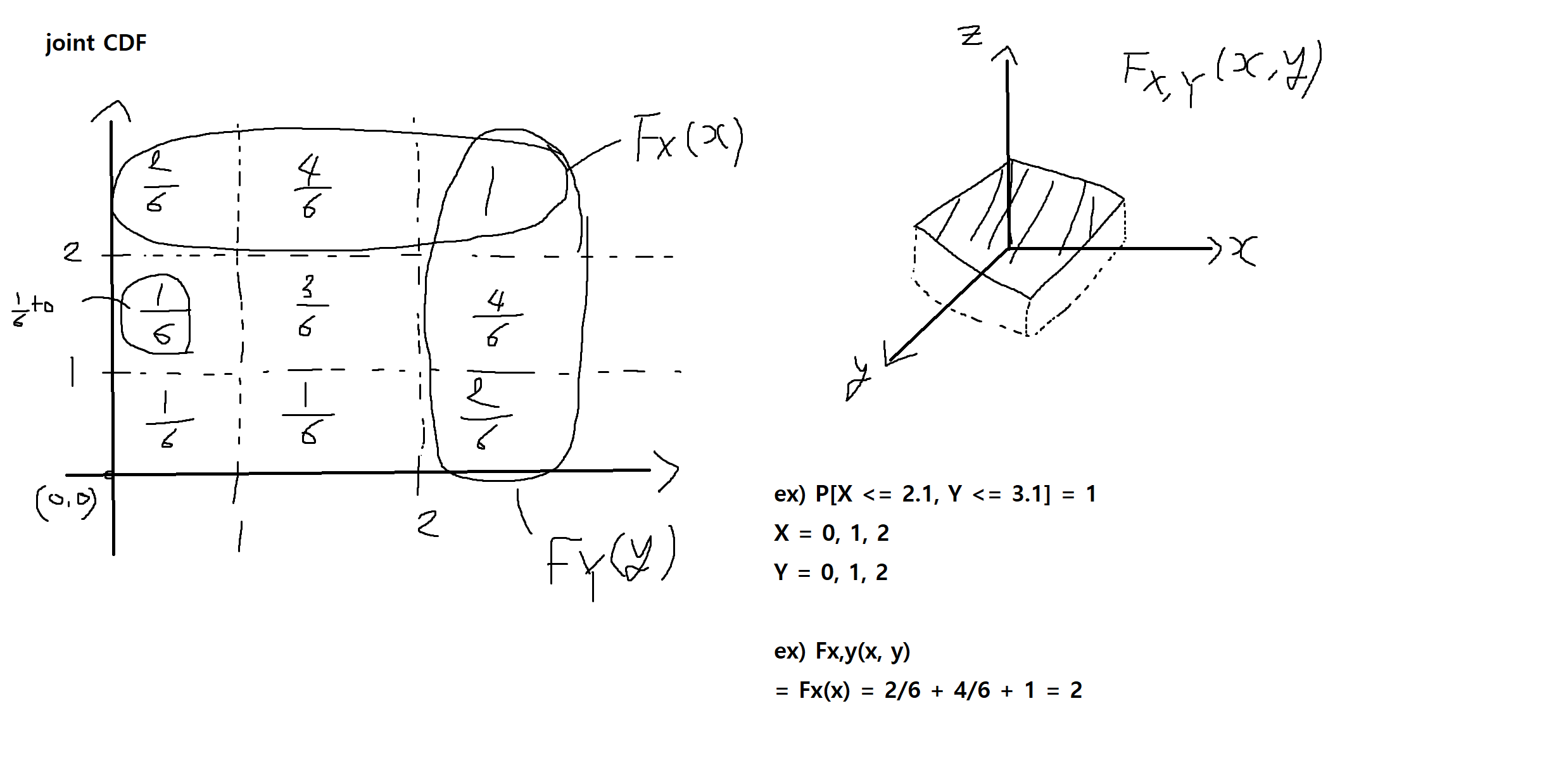
예제 5-6 : (X, Y)의 결합누적분포함수가 다음과 같다. (단 α >0, B > 0)

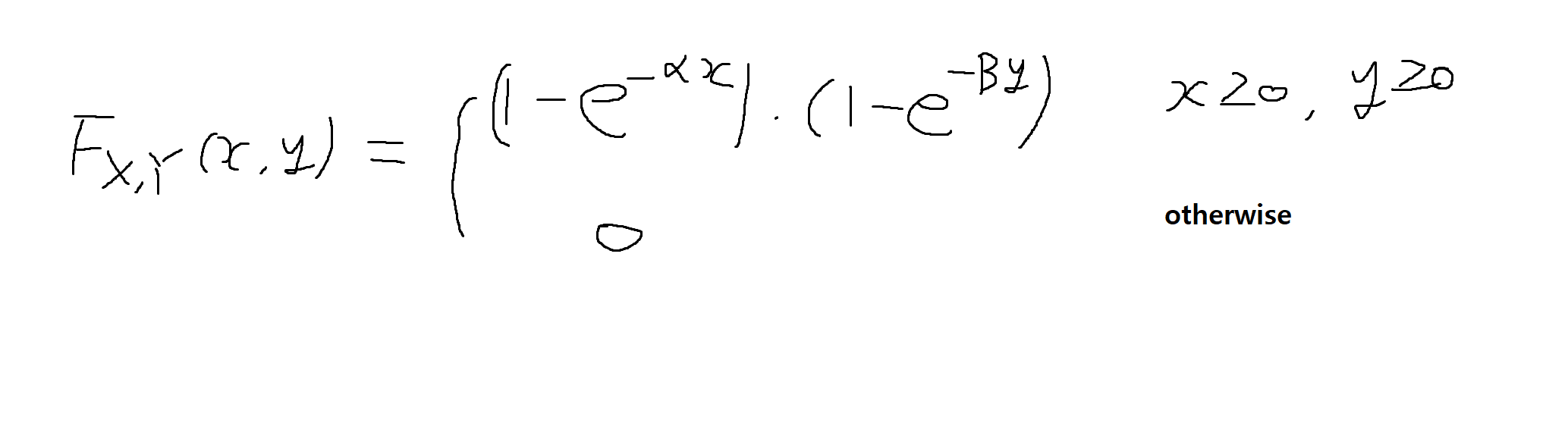
(1) X, Y의 한계누적분포함수(marginal CDF)

Fx(x) = Fx,y(x, ∞) = (1 - e^(-αx))
-> y = ∞일 때 e^(-By) = 0)

Fy(y) = Fx,y(∞, y) = (1 - e^(-βy))

(2) 각 사건의 확률값 : A = {X <= 1, Y <= 1}, B = {X > 1, Y > 1}, C = {1 < X <= 2, 2 < Y <= 5}

P[A] = Fx,y(1,1) = (1 - e^(-α)) * (1 - e^(-β))

P[B] = 1 - Fx(1) - Fy(1) + Fx,y(1,1)

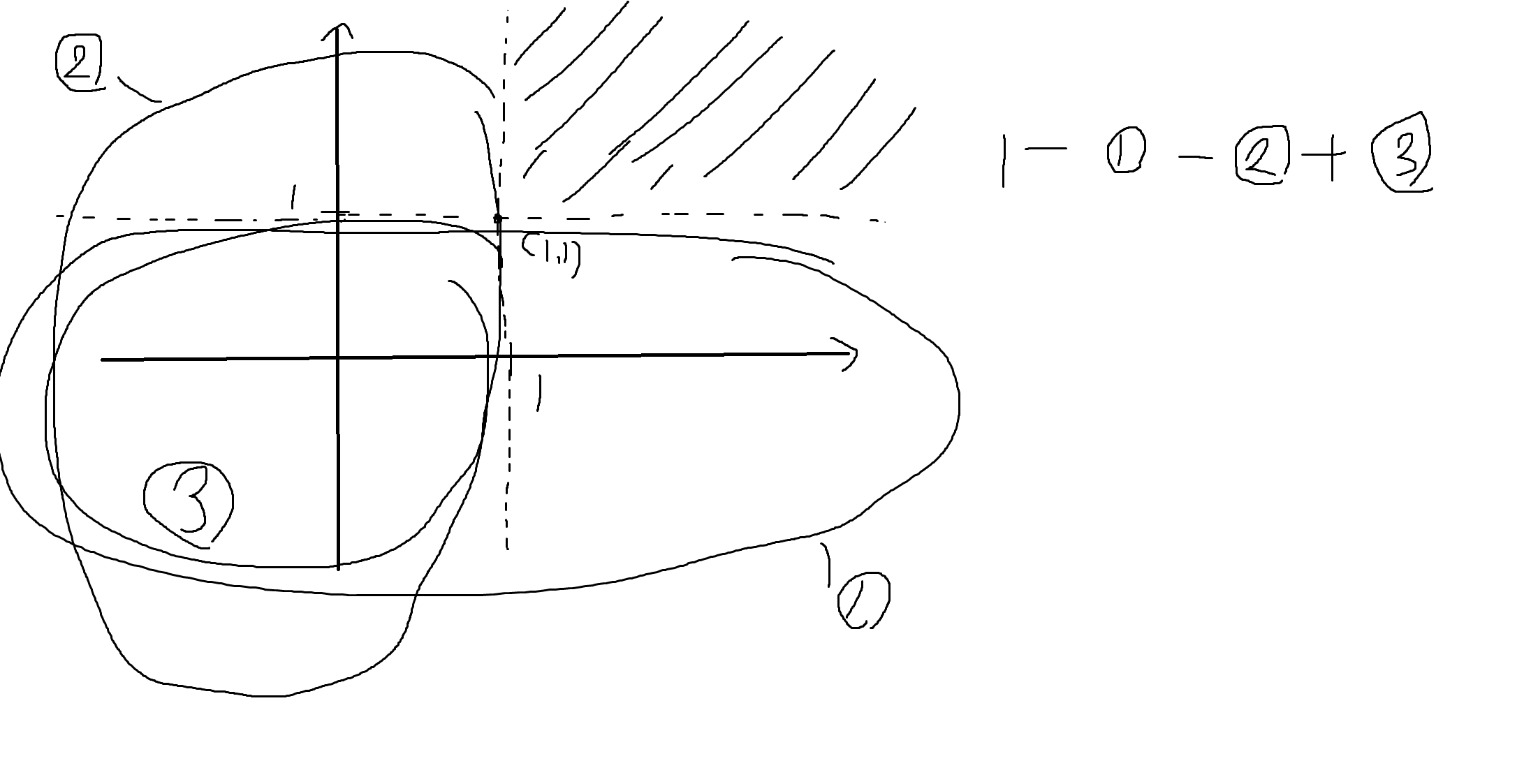
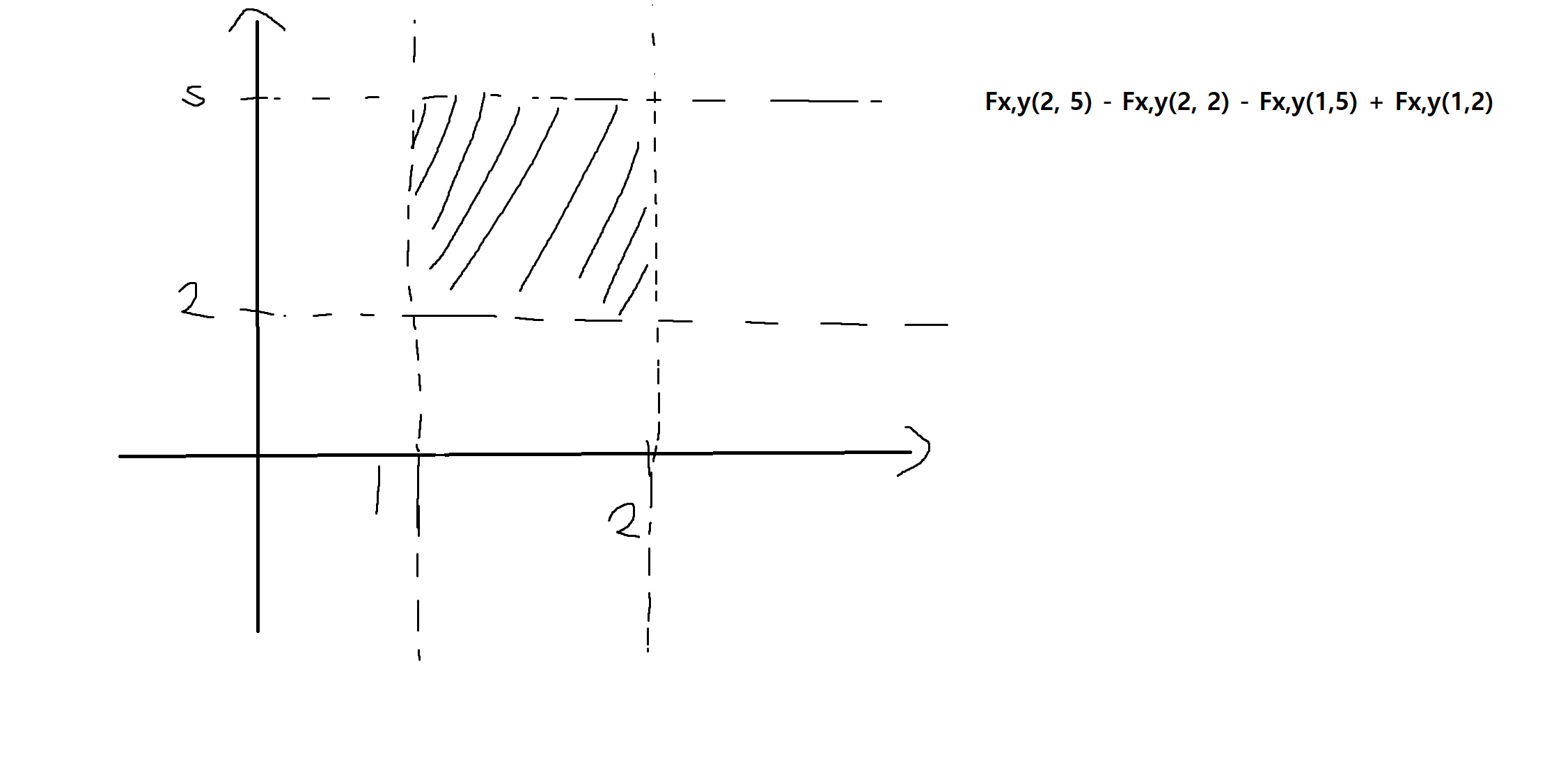
P[C] = Fx,y(2, 5) - Fx,y(2, 2) - Fx,y(1,5) + Fx,y(1,2)

예제 5-7 : 반경이 R0인 과녁에 화살을 균등하게 던질 때, 과녁에서의 화살의 위치를 (X, Y)라고 하자. 이때 과녁중심(원점)과 (X, Y)사이의 거리와 각도(radian)를 각각 R, Θ라고 할 때, 다음을 구하여라

(1) R, Θ의 결합누적분포함수(joint CDF)

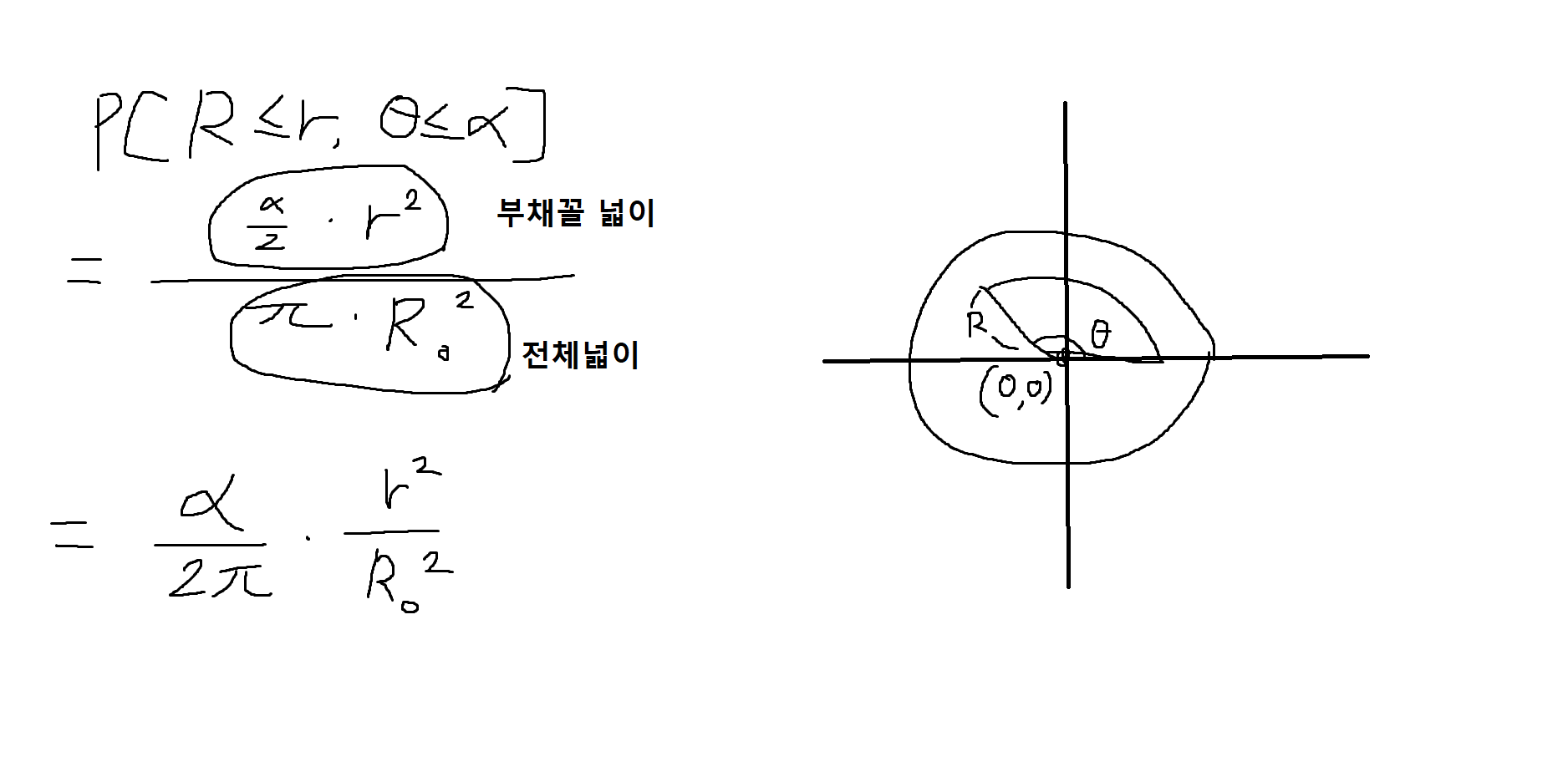
(2) R, Θ의 한계누적분포함수(marginal CDF)

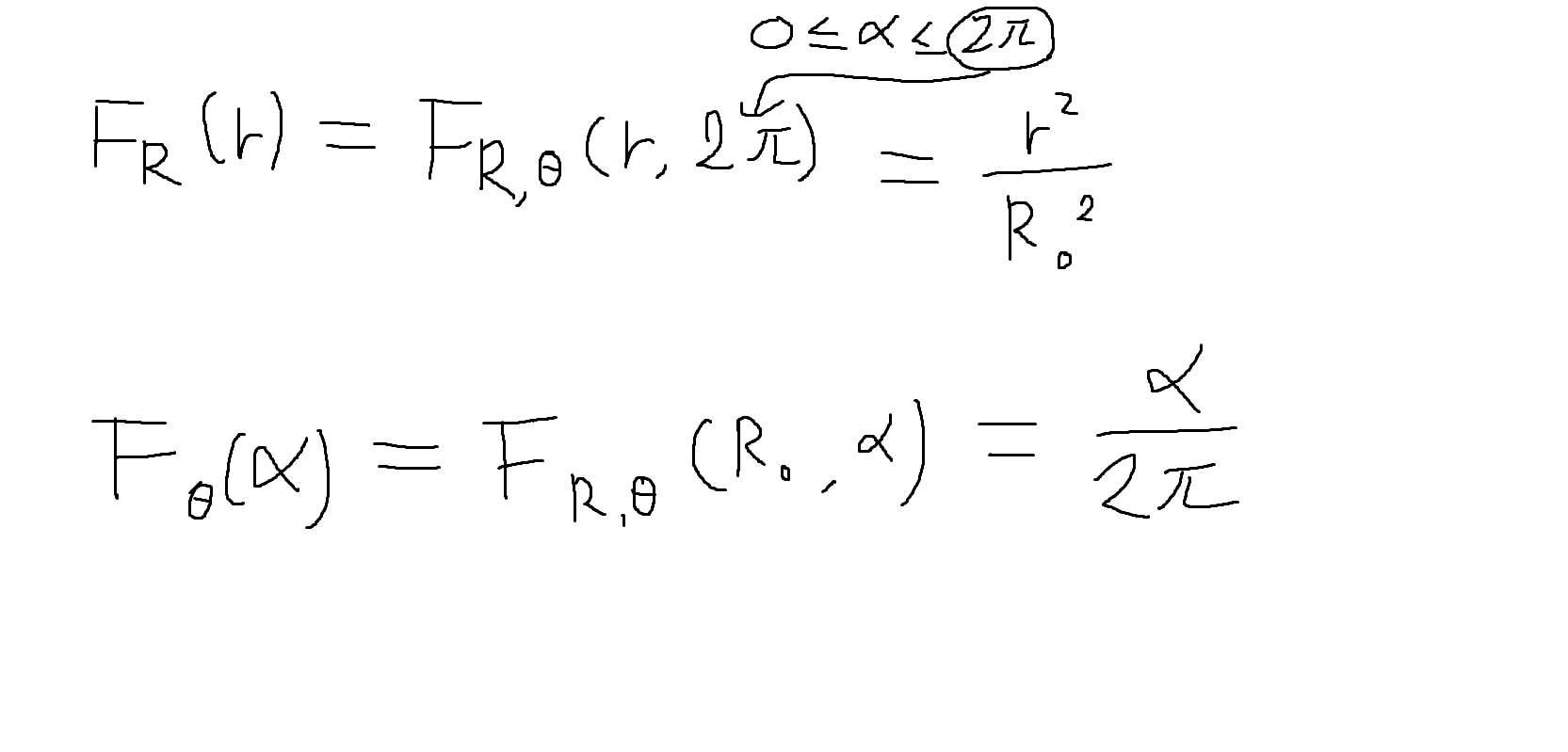
(3) 화살이 1사분면이면서 반경이 0.5 R0보다 큰 구역에 위치할 확률

---

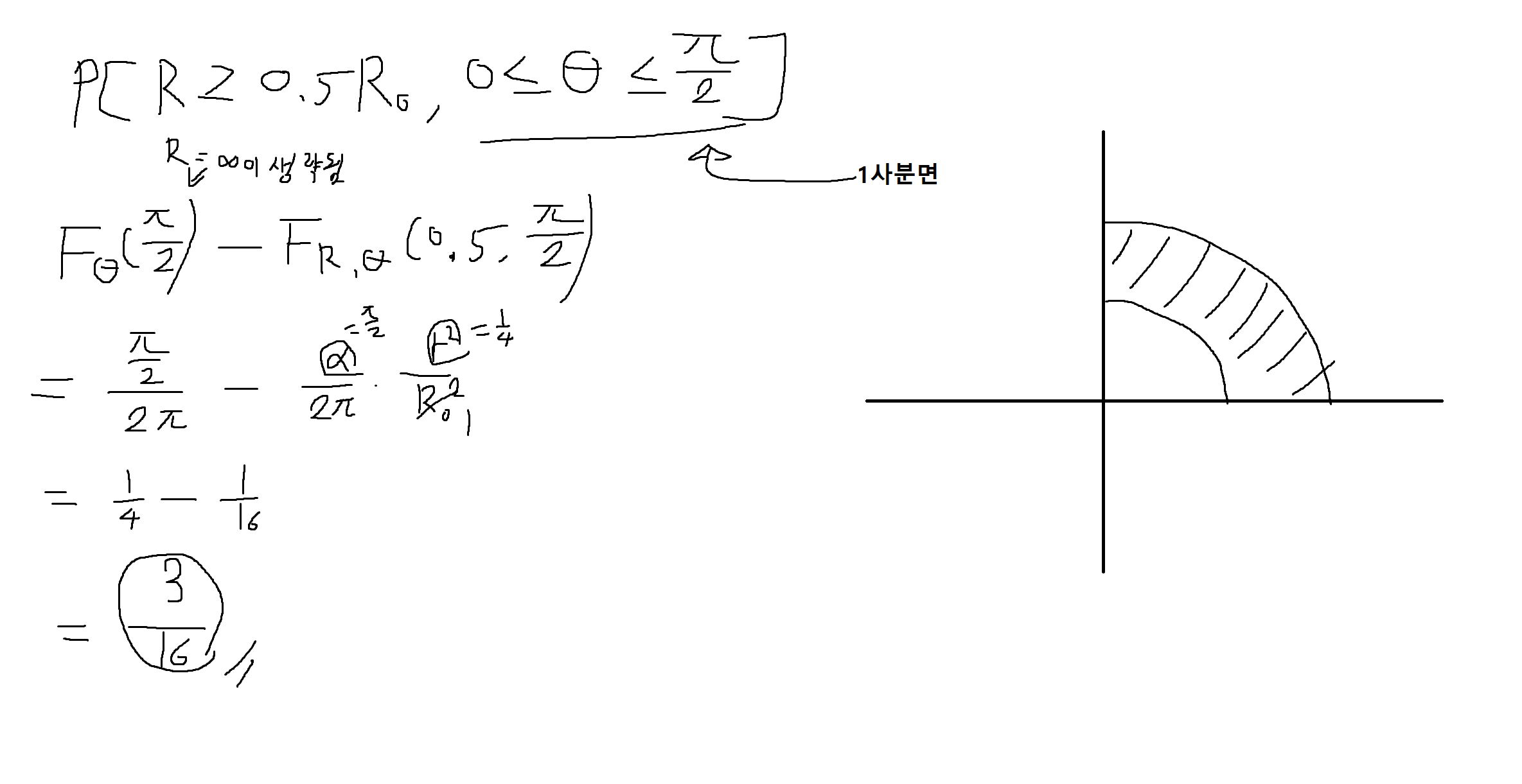
• 확률밀도함수(PDF): 확률변수 X의 누적분포함수(CDF) Fx(x)의 미분
  fx(x) = d/dx Fx(x)

• 결합확률밀도함수 (joint CDF) : 확률변수순서쌍(X, Y)의 결합누적분포함수(joint CDF)
  -> Fx,y(x, y)의 미분
  

---

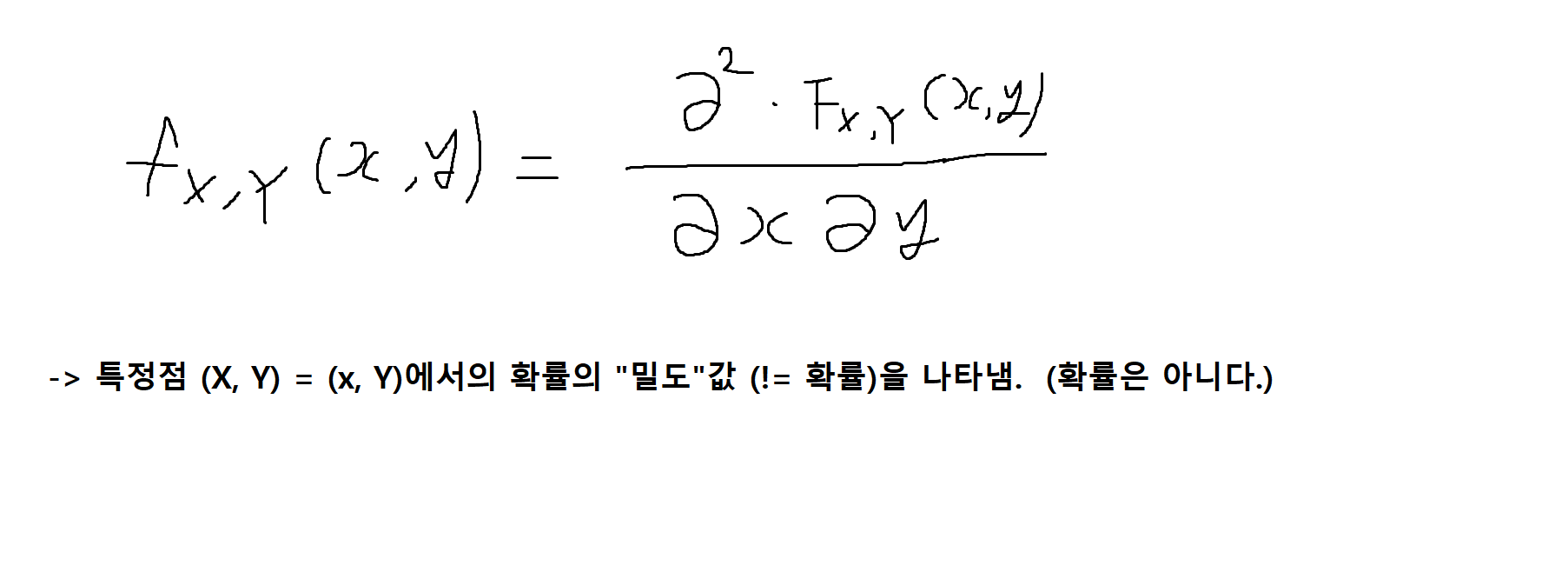
• (복습) 확률밀도함수 (PDF)의 특성 (확률변수 X)
  

---

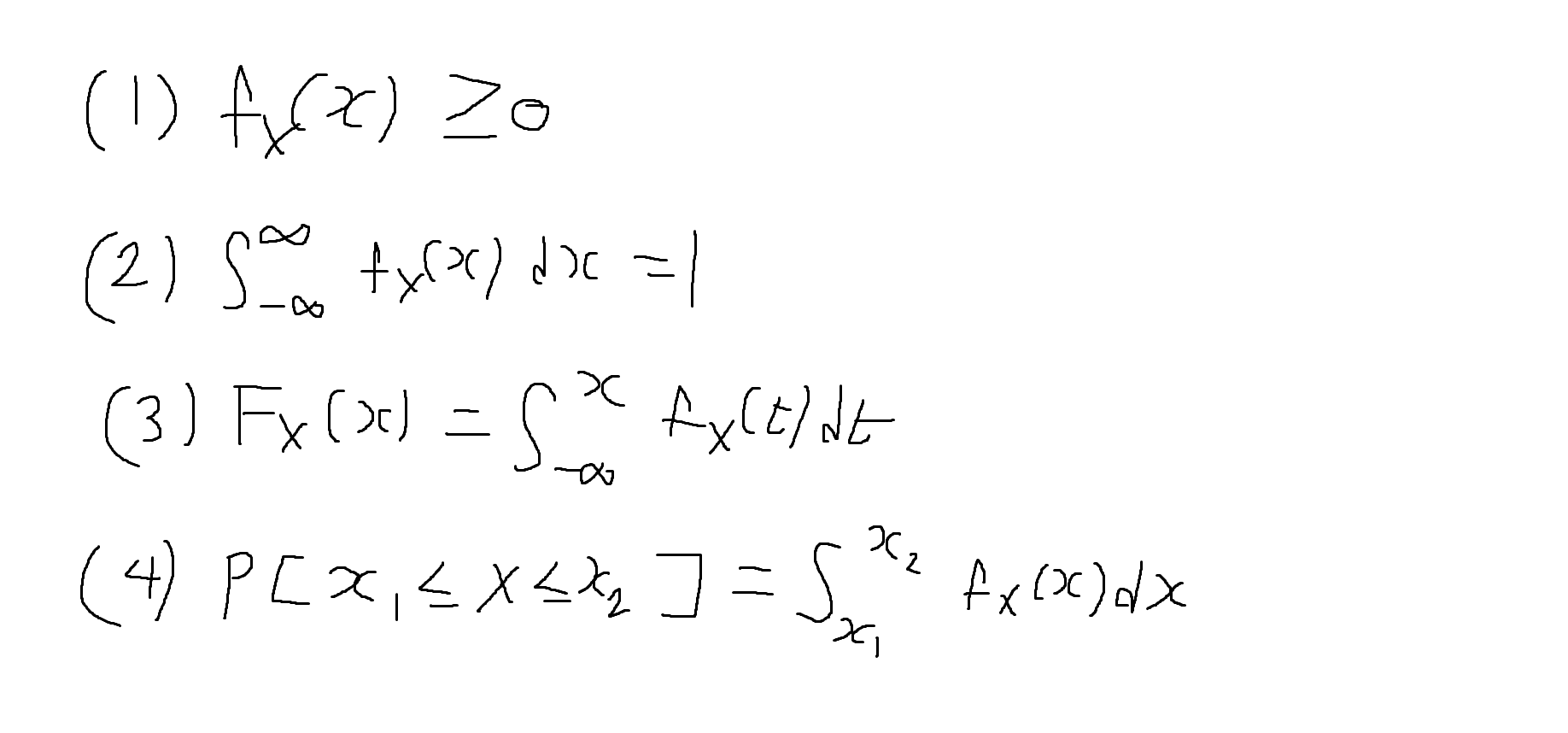
• 결합확률밀도함수(joint PDF)의 특성 : 확률변수의 순서쌍 (X, Y)
  

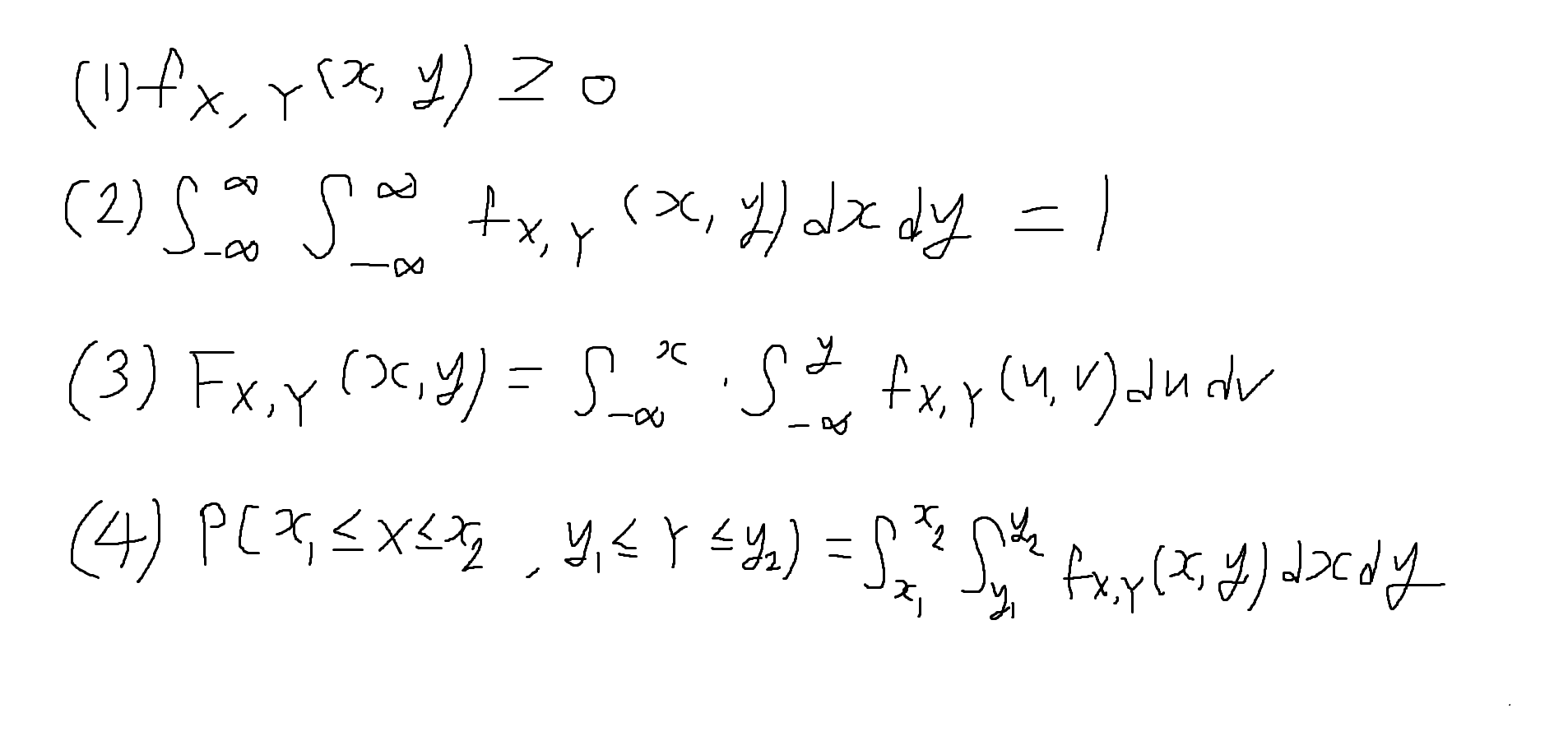
• 한계확률밀도함수 (marginal PDF)
  -> 결합확률밀도함수에서 제거하고자 하는 확률변수의 전체 범위를 계산
  

예제 5-8 : 단위 사각형에서 무작위로 선택된 점 (X, Y)는 아래의 균등결합밀도함수(joint PDF)를 가진다. 이때, (X, Y)의 결합누적분포함수(joint CDF)를 구하여라.

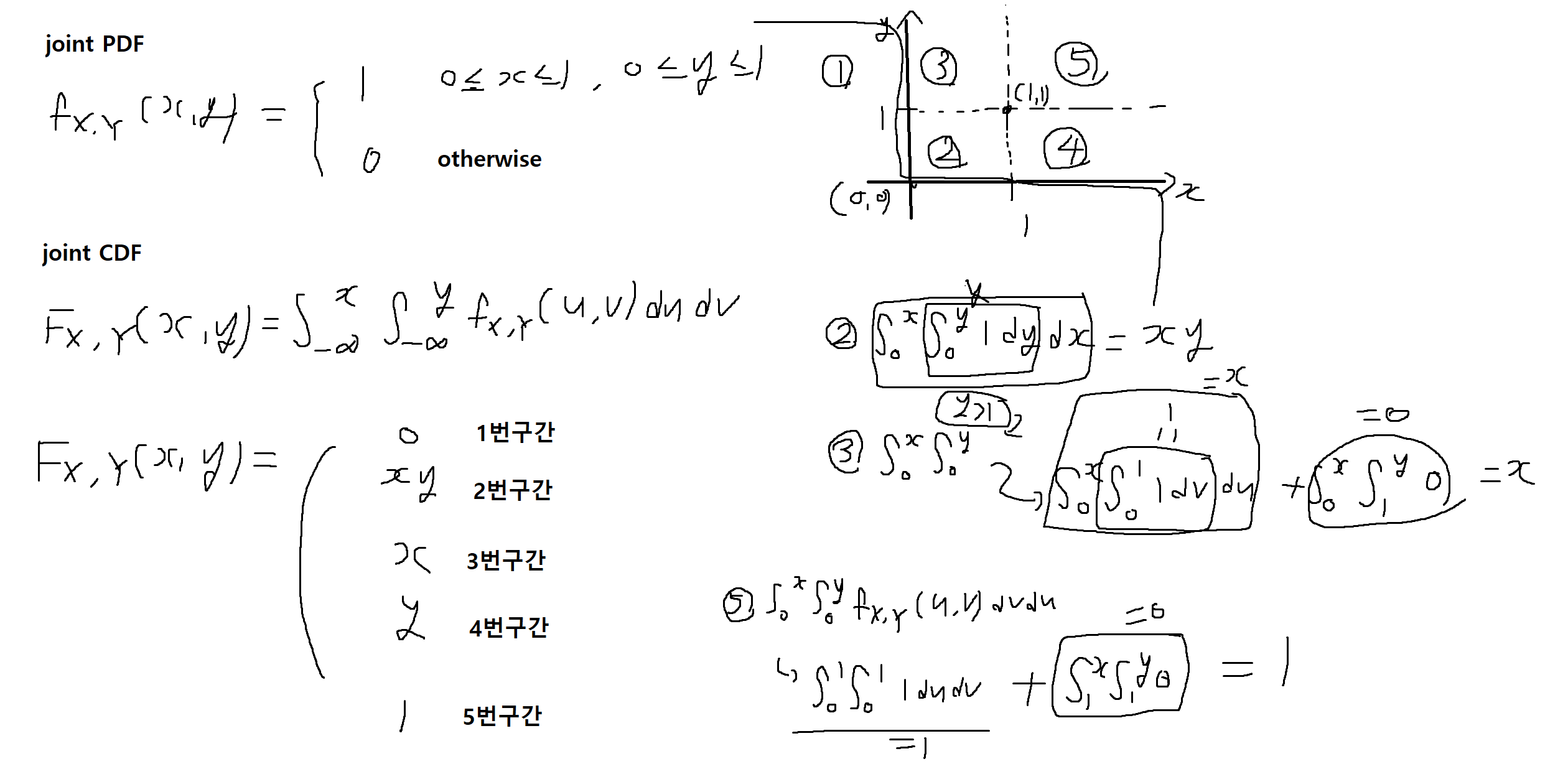
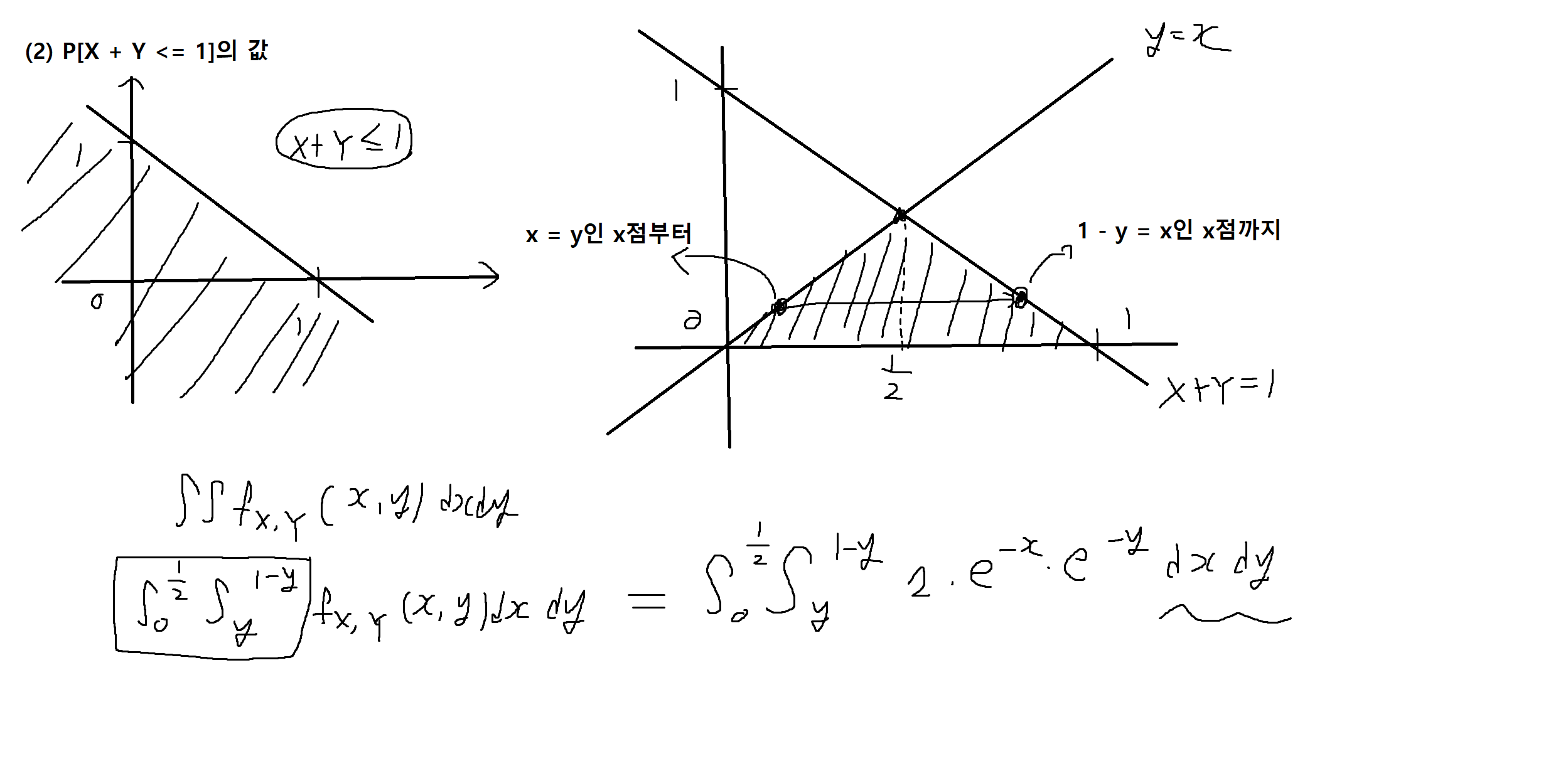
예제 5-9 : 아래의 fx,y(x, y)가 결합확률밀도함수(joint PDF) 일 때, 다음을 구하여라. (* Hint : 적분구간유의!)

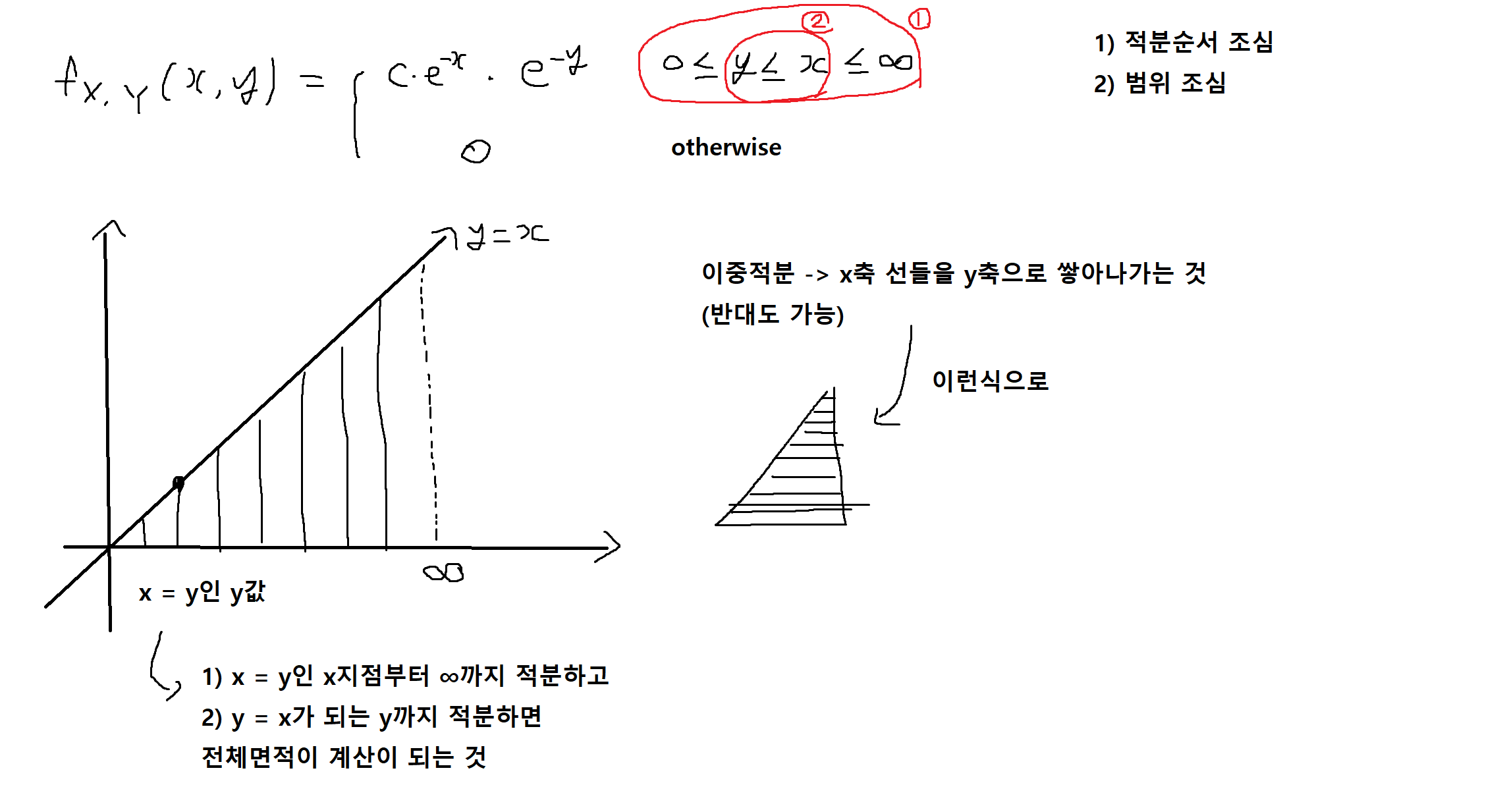
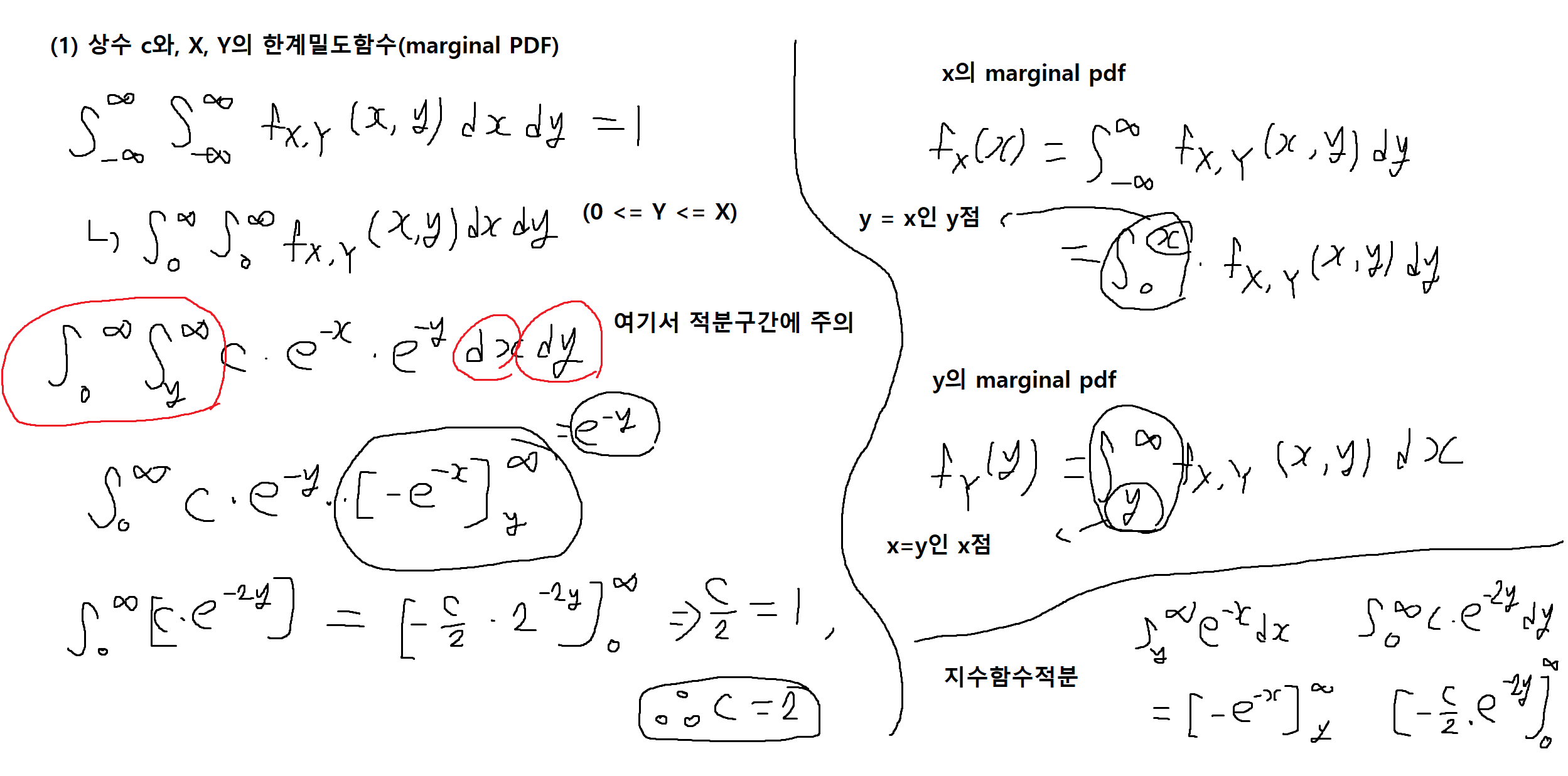
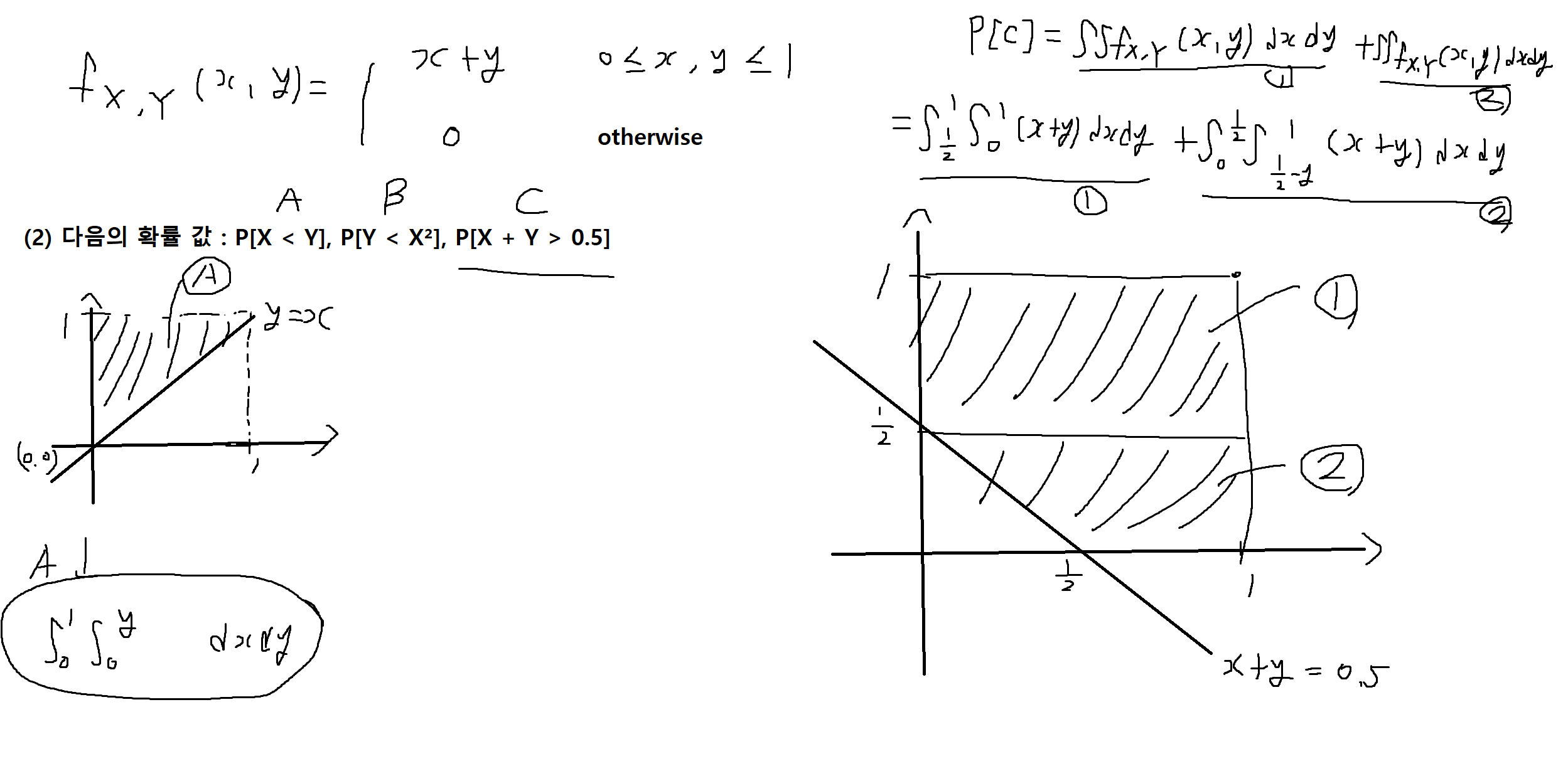
예제 5-10 : 아래의 fx,y(x,y)가 결합확률밀도함수(joint PDF) 일 때, 다음을 구하여라

---