MVD 와 4NF
MVD 란?
MVD 는 Multivalued Dependency 를 의미한다.
이전에 FD, Functional Dependency 는 Y = f(X) 를 의미하며 X → Y 로 표기하였다. MVD 는 FD 의 Generalization 인데 기존에 FD 에서 X 의 값에 대해 Y 값이 하나로 대응되었다면, MVD 는 말 그대로 대응되는 Y 값이 여러개로 일반화 되었기 때문이다.
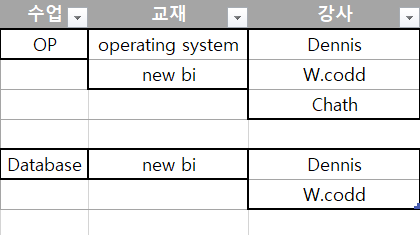
최초에 이러한 Relation 이 있었다고 생각해보자. 굵은 테두리로 감싸진 블럭이 하나의 attribute 내에 포함된 data 라고 생각하면 될 것 같다.
그렇다면 위의 Relation 은 1NF 를 만족하지 않는다. row-and-column 에 Repeating Group 이 존재하기 때문이다.
자세히 보면 교재와 강사는 서로 독립이다. 어떠한 종속도 존재하지 않는다.
어쨋든 1NF 로 normalization 하게 되면 각각의 교재에 강사들이 대응되게 표현 됨을 알 수 있다.
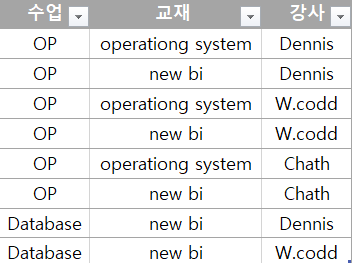
일단 1NF 를 만족하는 Relation CTX 가 만들어졌다. CTX 에서 어떠한 단일 Attribute 도 Primary Key 가 될 수는 없다. 또한 어떠한 2개 Attribute 로 표현된 Composite Attribute 도 Primary Key 가 될 수 없다.
따라서, CTX 의 Primary Key : { 수업, 교재, 강사 }
- No Repeating Group ( rows-and-columns ) → 1NF
- No Partial FD → 2NF
- No Transitive FD → 3NF
- No Partial FD → BCNF
CTX 는 BCNF 를 만족한다. 하지만 누가봐도 명백히 Redundancy 가 존재하고 이로 인해 Update Anomaly 가 발생하게 된다.
- Insert Anomaly 만약 수업 : OP 의 교재 : second Theory 를 추가하게 된다면 수업 : OP 를 진행하는 강사들에 대해 모두 레코드를 추가해주어야 한다. <OP, second Theory, Dennis>, <OP, second Theory, W.codd>, <OP, second Theory, Chath>
MVD 는 위와 같이 수업과 교재 혹은 수업과 강사 의 관계를 말한다. X → Y 에서 대응되는 Y 값이 여러개이며 Y 는 X 에 대해 잘 정의된 set 을 갖게 된다.
MVD?
R { A, B, C } 에서 다음 조건을 만족하면 B 는 A 에 Multidependent (A →→ B) 하다고 한다.
R 에서 주어진 { A-value, B-value } 에 대응하는 B-value 집합은 오직 A-value 에만 종속이지 C-value 에 대해서는 독립적이다.
이때 B-value 의 집합을 well-defined set 이라고 한다.
여기서 잘 보면 { A-value, B-value } 에 대응하는 B-value 집합이 A-value 에만 종속이므로 반대로 { A-value, C-value } 에 대응하는 C-value 집합이 A-value 에만 종속이고 B-value 와는 자동으로 독립임을 알 수 있다.
따라서 MVD : A→→B iff A→→C 이다. 이를 MVD : A →→ B | C 로 표현한다.
즉, MVD 는 Relation 내에 배타적인 두 Attribute 집합이 함께 있을 때 성립하는 제약 조건이다. MVD 는 위에서 1NF 를 변환하는 과정에서 나타났듯이 어떠한 조건을 만족하는 Tuple 이 Relation 내에 있기를 요구한다.
MVD, 다치 종속은 Tuple 이 만들어내는 종속으로 분류한다.
<OP, second Theory, Dennis>
<OP, second Theory, W.codd>
<OP, second Theory, Chath>
교재 : second Theory 가 추가되면 well-defined 된 강사 set 을 요구하는 것.
MVD 는 하단 조건 중 하나를 만족하는지의 여부에 따라 Non trivial MVD 와 Trivial MVD 로 분류된다.
MVD : X →→ Y 에 대해,
-
Y 가 X 의 부분집합임을 의미한다.
-
X 와 Y 를 합친 Attribute set 이 Relation R 의 모든 Attribute set 을 표현해야 함을 의미한다.
바람직하지 못한 NTMVD(Non Trivial MVD)는 위에서 본 CTX 와 같이 Redundancy 와 이로인한 Update Anomaly 를 발생시킨다.
바람직하지 못한 NTMVD 를 TMVD 로 만들거나 4NF 의 조건을 만족시키는 방향으로 relation 을 decompose 하여 redundancy 를 제거 할 수 있다!
4NF - Remove Non Trivial MVD
이전 CTX relation 은 왜 TMVD 가 아닐지를 다시 한번 따져보자.
CTX 는 relation R { 수업, 교재, 강사 } 에 대해 MVD : 수업 →→ 교재 | 강사 를 가진다.
하지만, 수업과 교재의 합집합이 R 의 전체 attribute set 이 아니며 수업 attribute 가 교재의 super set 또한 아니므로 CTX 는 NTMVD 를 가진다.
4NF
4NF 는 바람직하지 못한 NTMVD 를 제거하는 normalization 이다.
4NF 는 Relation R 에서
- NTMVD : A →→ B 가 있을 때 B 를 제외한 R 의 모든 attributes 가 A 에 대하여 Functionaly Dependent 하면 R 은 4NF 하다고 한다.
- 모든 MVD : A →→ B 가 있을때 모든 MVD 가 Trivial MVD 일 경우 R 은 4NF 하다고 한다.
4NF 의 정의를 바탕으로 CTX 가 4NF 를 만족하지 못하는 이유는 하단과 같다.
-
relation CTX { 수업, 교재, 강사 }
-
NTMVD : 수업 →→ 교재 존재
-
FD : 수업 → 강사 만족하지 않음.
수업과 강사의 관계는 FD 가 아닌 MVD 이다. 따라서 CTX 는 4NF 가 아님이 된다.
그렇다면 어떻게 4NF 를 만족하도록 하게 할 수 있을까?
정의를 보았을때
- MVD : 수업 →→ 교재 를 trivial 하게 바꾸던지
- MVD : 수업 →→ 강사 를 FD : 수업 → 강사가 되도록 해야한다.
하지만 2번의 방법을 수행할 수 없다. 왜나면 수업은 강사를 특정 할 수 없기 때문이다.
따라서 1번의 방법을 적용하기 위해 다중값을 결정하는 속성인 수업을 기준으로 relation 을 decompose 한다.
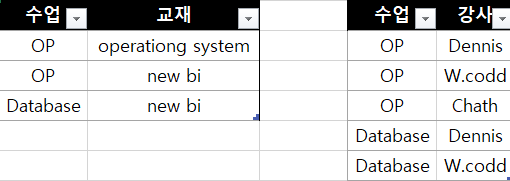
자, 다시 한번 decompose 된 relation 이 4NF 를 만족하는지 확인해보자.
- 수업-교재 relation MVD : 수업 →→ 교재 는 수업교재 = R 을 만족하므로 Trivial MVD 이며 이는 4NF 를 만족
- 수업-강사 relation 위와 동일.
수업-교재와 수업-강사 에서는 { 수업, 교재 }, { 수업, 강사 } 가 Candidate Key 이며 Trivial MVD 이다.
4NF 를 만족함은 확인하였다. Update Anomaly 의 제거 여부를 확인하자.
- Insert Anomaly 만약 수업 : OP 의 교재 : second Theory 를 추가하게 된다면 수업-교재 relation 에만 <OP, second Theory> 를 추가한다.
Join Dependency 와 5NF
Join Dependency
Join Dependency 는 Constraint nD(n-decomposable Constraint) 라고도 하는데, 어떠한 Relation 이 Join Dependency 를 만족하면 해당 Relation 은 n-decomposable 이라고 한다.
Join 연산은 Cartesian Product 에 근본을 두고 있다. Cartesian Product 를 수행하되 공통 Attribute 가 존재하면 해당 Attribute 를 기준으로 연산을 수행한다.
Join Dependency?
만약 R (A, B, C, ... , Z) 가 각각의 Projection AB, BC, CD, ... , ZA 의 Join 과 같다면 JD * (AB, BC, ... , ZA) 를 만족한다고 한다.
즉 Projection 된 relations 를 공통 attribute 를 기준으로 join 한 결과가 원래의 Relation 과 같아야 한다는 의미이다.
이 말은 Join 된 결과가 원래의 Relation 보다 더 많은 Attribute 나 적은 Attribute 를 가져서도 안되고 Record 또한 일치해야 한다는 의미이다.
- Loss Less Join (무손실 조인)
- Non Additive Join (비부가적 조인)
자 5NF 를 알아보기 전에 Join Dependency 의 예시를 확인해보자.
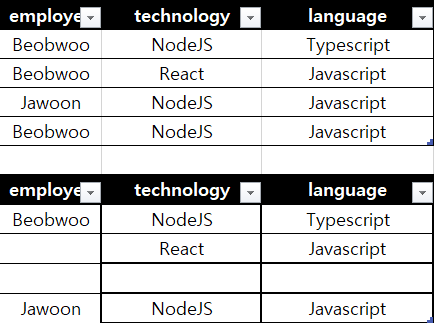
relation ETL(employee, technology, language)는 Primary Key 로 PK : { employee, technology, language } 를 가진다.
Non Trivial FD 도 없고 MVD 도 없다.
하단의 relation 을 확인, 두 attribute 가 독립이어서 Cross Product 의 결과가 ETL 에 나타나는 경우가 없음.
relation ETL 이 Join Dependency 를 만족하는가?

ET(employee, technology) JOIN TL(technology, language) JOIN EL(employee, language) == ETL(employee, technology, language)
JD 를 만족함을 알 수 있다. 하지만 ETL 에서 Tuple : <Beobwoo, NodJS, Typescript> 을 제거하면 Projection 된 relation 들의 Join 결과과 ETL 과 같지 않으므로 Join Dependency, 3-Decomposable 하지 않다.
이렇게 3-decomposable 하지 않은 relation 은 어떤 tuple 값을 삭제하거나 삽입하는 과정에서 Update Anomaly 가 발생 할 수 있어 계속해서 확인해야 한다.
그렇다면 어떻게 Projection 하고 Join 해야 JD 를 만족하게 할 수 있을까?
5NF - Projection Join Normal Form
5NF
5NF 는 주어진 Relation R 에서 모든 JD 가 Candidate Key 에 의해 Imply 되어야 함을 제약한다.
Imply 의 뜻?
Candidate Key 를 기준으로 Projection 되어야 한다. Candidate Key 를 기준으로 Projection 된 하위 relation 은 Join 할 경우 공통 attribute 가 Candidate Key 가 될 것이다.
위의 ETL 의 Candidate Key 는 CK : { employee, technology, language } 이다.
따라서 ET, TL, LE 는 JD 를 만족할 수 없으며 5NF 가 아니다.
5NF 에 대하여 ...
5NF 는 이상적인 Normal Form 으로 보인다.
/ 작성 중 /

