Functional Dependency(FD)

Functional Dependency 란?

functional-함수, dependency-종속 이라는 두 단어를 통해 연상해보면 어떠한 종속성이 존재하는데 그 종속의 형태가 함수의 성질이 아닐까 하고 추측 할 수 있다.

Functional Dependency

relation R 과 R 의 attributes subset X, Y 에 대해 FD 를 다음과 같이 정의한다.

Y is functionally dependent on X iff each X value in R has associated with

precisely one Y value in R

위의 FD 를 X→Y in R 로 표현하는데, 이는 함수에서 y = f(x) 를 생각하면 쉽게 이해 할 수 있다.

x 의 값에 하나의 y 값이 대응되는것, 이러한 관계가 R 의 attribute subset 간에 적용되는 것을 FD 라고 한다.

조금 더 구체적으로,

X → Y iff , every possible legal value of R , each X value has associated with

precisely one Y value in R

every possible legal value → whenever two tuples agree on their X value, they also agree on their Y value.

R 내의 모든 가능한 값에 대해서 위에서 정의한 X → Y 가 성립해야 FD 가 성립한다는 이야기이다.

앞으로 추가될 수 있는 레코드(tuple)를 포함하여 X 에 대한 Y 의 값이 오직 하나여야 FD 를 만족한다는 이야기.

Candidate Key 와 FD

X 가 만약 R 의 candidate Key 라면 R 의 모든 attribute 는 X 에 대한 FD 가 성립해야 한다.

R = { X, Y, Z } 라면 X → { Y , Z } == X → Y && X → Z 가 성립해야 한다.

만약 X 가 CK 임에도 불구하고 FD 가 성립하지 않는다면 이 Relation R 에는 Redundancy 가 발생하게 된다.

Functional Dependent 의 Closure

Closure 란?

우리말로는 "폐포" 라고 한다. 기존의 관계 혹은 규칙을 유지하면서 새로운 성질을 갖도록 하는 것을 말하는데, Functional Dependent Closure 에서 말하는 기존 관계 혹은 규칙은 당연히 FD 이다.

어떠한 도메인 내에서 연산이 수행되었을때 그 결과 또한 도메인 내에 위치 할 수 있도록 하는 관계적 성질로 나는 이해하였다.

Fuctional dependent Closure

Relation R 의 FD set 을 S 라고 할 때 closure S+ 는 S 로 유도된 모든 FD 집합을 말한다. S 로 부터 유도된 S+ 를 구하기 위한 추론 규칙들의 집합을 Armstrong's axioms 라고 한다.

즉, FD 의 "규칙 혹은 관계" 를 유지하면서 새로운 "성질" 을 추가 하기 위해서는 Armstrong's axioms 에 따라 기존 FD 를 확장해야 한다는 것이다.

Armstrong's axioms

1. Reflexive Rule : if B is subset of A, A → B

trivial FD 라고도 한다. 

2. Augmentation : if A → B , then AC → BC

   약간 양변에 상수값 곱해져도 방정식이 성립하는 느낌

3. Transitivity : if A → B, B → C then A → C

   추론 규칙이다.

4. Self Determination : A → A

5. Decomposition : if A → BC then A → B, A → C

6. Union : if A → B, A → C then A → BC

AA(Armstrong's Axioms) interface rule 을 통해 주어진 FD 가 closure 가 있는 지를 결정 할 수 있다.

예를 통해 위의 내용을 다시한번 리마인드 해보자. K 를 R 의 Super Key 라고 하자. Super Key = Candidate Key + Reducible Attributes 이다. K 가 R 의 Super Key 인지를 결정하기 위해 K 에 FD 인 모든 R 의 attributes 집합을 closure K+ 로 표현한다.

FD : A → BC, E → CF, B → E, CD → EF 이고 K = AD 일 때 K → {A, B, C, D, E, F} 인가?

답은, K = AD → A 할 수 없기 때문에 Super Key 가 아니다.

Update Anomaly (갱신 이상)

관계형 DB 에서 relation 내에 존재하는 Redundancy 에 의해 다양한 Update Anomaly 가 발생하게 된다. 즉, Update Anomaly 는 relation 내의 data redundancy 로 인해 발생하는 문제를 말한다.

그렇다면 Update Anomaly 는 어떠한게 있을까?

• Insertion Anomaly 불필요한 데이터를 함께 삽입하지 않으면 데이터 삽입이 불가능한 문제점

  → 데이터 삽입시 원치 않는 데이터를 함께 삽입해야 한다는 의미. 이를 Dirty Data Insertion 이라고 한다.

• Modification Anomaly 중복된 데이터 가운데 일부만 수정되어 데이터 불일치 문제가 발생하는 문제점
  → Data Inconsistency 라고 한다.

• Deletion Anomaly 데이터 삭제시 다른 유용한 데이터 또한 함께 삭제되는 문제점
  → Lost Data 라고 한다.
  
  

Normalization : 1NF, 2NF, 3NF, 4NF

Normalization 이란?

• Unormalized Relation Relation 의 모든 row 와 column 에 repeating group 을 값으로 갖는 경우이다. 이는 행 단위로 본 tuple 이 repeating group 을 갖거나 열 단위로 본 attribute 내의 값이 repeating gruop 을 갖는 경우들을 전부 포함한다.
  
• Normalized Relation Normalized relation 은 atomic 값만 갖고 있는 경우이다.
  

normalization 은 하단의 방법을 통해 normalized 된 relation 을 만드는 데이터 베이스의 데이터 재구성 과정이다.

1. 데이터의 redundancy(repeating group)을 제거하거나 최소화
2. 데이터 종속이 논리적으로 표현되도록 관련된 모든 데이터 구성요소들을 함께 저장 표현 하여 data anomaly 제거

normalization 은 1NF 부터 5NF 까지 Anomaly 문제를 해결한 테이블 설계를 말한다.

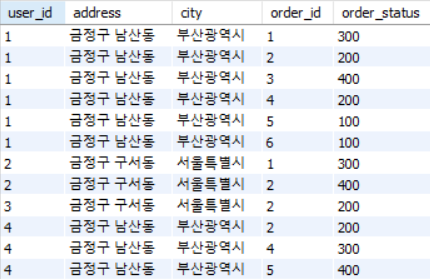
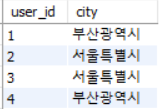
이런 테이블 first_normal_form 이 있다고 가정하자.

first_normal_form FD :

1. { user_id, order_id } → address
2. user_id → city
3. city → address
4. user_id → address
5. order_id → city

위의 relation 은 많은 redundancy 가 발생하고 이로 인해 update anomaly 가 생긴다. 여기서 Insert, Update, Delete 모두에 대해 anomaly 가 발생하는데, 각각을 설명하면 다음과 같다.

1. Insert Anomaly

   만약 새로운 사용자를 추가하려고 하면 사용자의 정보만을 가지고 추가 할 수 없다.

   <user_id, address, city, dummy_order_id, order_status>

   가짜 데이터, dummy_order_id 를 사용해야 사용자 정보를 추가 할 수 있는데 이는 dirty data 이다.

2. Update Anomaly

   city → address 라는 FD 가 있음에도 불구하고 특정 사용자의 address 만 변경 하게 될 경우 중복된 같은 도시의 address 는 변경되지 않는다.

   <1, '금정구 남산동', '부산광역시', 3, '400'> 의 address 를 '서구 부전동' 으로 변경하게 될 경우 user_id : 2, 3, ... 의 FD : city → address 가 inconsistency 하게 된다.

3. Delete Anomaly

   FD : city → address 임에도 불구하고 user_id : 2, 3 을 삭제하게되면 '부산 광역시' → '금정구 구서동' 이라는 데이터가 아예 relation 에서 제거되는 Lost data 가 발생한다.

1NF (First normal form) - Atomic Value

1NF 는 Relation 이 Scalar 값만 갖는 경우로서 Repeating Group 을 attribute 값으로 갖지 않는 경우이다.

{ user_id, order_id } → order_status 인 FD 에서 <1, 3, (100, 343)> 와 같은 경우에는 attribute 값에 중복될 수 있는 값이 오므로 atomic 하지 않다.

First Normal Form 은 relation 의 모든 row-and-column 의 값이 오직 scalar 값만 갖는 경우이다.

위에서 예시로 보여준 first_normal_form 은row-and-column 의 값이 오직 scalar 값만 갖기 때문에 1NF 를 만족한다.

2NF (Second normal Form) - No Partial FD

2NF 는 1NF 이고 모든 nonkey attribute 가 Primary Key 에 대하여 irreducibly dependent 한 것을 말한다.

irreducibly dependent 는 primary key 의 subset 에 대하여 다시 FD 가 성립하지 않는다는 의미이다. 즉, 이미 primary key 는 FD 를 성립 시키기 위한 최소한의 attribute set 이라는 의미.

( Candidate Key 의 정의에서 2번째 요건으로 Minimality 에 대해 이야기 한 것 과 같은 맥락으로 이해 )

⇒ No Partial FD

처음에는 단순히 "아 PK 의 subset 으로 FD 가 성립 하지 않으면 되는 구나" 했는데 이 말이 부분 종속이 있으면 안된다는 말임을 알게 되었다.

부분 종속(Partial FD)이란 기본키가 { A, B } → 나머지 일 때 A → 특정 몇개 인 경우를 말한다.

이렇게 되면 기본키에 A 로만 결정 할 수 있는 컬럼들이 있는데 다른 컬럼들을 결정하기 위해 B 를 추가 한 것이므로 당연히 redundancy 가 생길 수 밖에 없다.

이런 경우를 해결하기 위해 테이블을 분리하여 처리한다. 분리하는 기준은 A → 특정 컬럼 몇개 인 경우 A 와 특정 컬럼 몇개 를 묶고 나머지를 B 와 묶으면 될 것이다.

위의 예시는 1NF 는 만족하지만 FD : { user_id, order_id } → city 인데 user_id → city 또한 만족하므로 Partial FD 가 존재하게 된다.

어떻게 Partial FD 를 제거하여 2NF 를 만족 시킬 수 있을까?

relation 을 decomposition 함으로서 해결 할 수 있다.

first_normal_form(user_id, city, address, order_id, order_status) 를 user(user_id, address, city) 와 order(user_id, order_id, order_status) 로 decomposition 하면 Partial FD 가 사라진다.

실제로 확인해보자!

1. { user_id, order_id } → order_status
   1. order relation 에서 No Partial FD 이므로 OK
2. user_id → city
   1. user relation 에서 No Partial FD 이므로 OK
3. city → address
   1. No Partial FD, OK
4. user_id → address
   1. No Partial FD, OK
5. order_id → city
   1. No Partial FD, OK

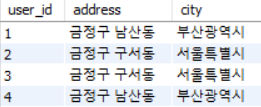
first_normal_form relation 에서 중복되었던 많은 데이터가 제거됨을 알 수 있다.

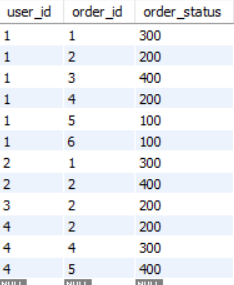
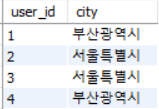
즉 1NF 에서 2NF 로 normalization 하는 방법은 Partial FD 에 대해 relation 을 decomposition 하여 Partial FD 를 제거하면 된다.

3NF (Third normal Form) - No Transitive FD

3NF 는 2NF 이고 모든 Nonkey attribute 가 Primary Key 에 대하여 Non Transitive dependent 한 것을 말한다.

transitive dependent 는 FD: user_id→ city, city → address 이면 user_id→ address 인 관계를 말한다.

3NF 는 no transitive dependent 이면서 no partial dependent 이므로 반드시 Primary Key 에 의해서만 FD 가 성립해야 한다는 이야기 이다.

R 의 FD : A → B, B → C, A → C 가 있을 때, FD 의 관점에서는 틀리지 않았다. 하지만 A → C 보다는 B → C 가 더 논리적으로 맞는 경우가 있따.

이런 경우에는 이행 종속을 제거하기 위해 마찬가지로 테이블을 분리하여 { A, B } , { B, C } 로 처리한다.

이행 종속을 왜 제거하는 걸까?

user relation 에서 key 는 user_id 이다. 하지만 FD : user_id → city , city → address, user_id → address (Armstrong's axioms) 이므로 city → address 의 FD 를 가짐에도 새로운 도시와 세부 주소를 입력하고 싶을때는 user_id → address 의 FD 도 만족시키기 위해 가짜 user_id 를 사용해야 함을 알 수 있다.

→ Insert Anomaly 발생.

또한, user_id : 2, 3 을 제거하는 순간 '부산 광역시' → '금정구 구서동' 이라는 FD : city → address 의 데이터가 사라지게 되는 Lost Data 가 생긴다.

→ Delete Anomaly 발생.

마지막으로, '부산 광역시' → '서구 부전동' 으로 수정하게 될 경우 FD : city → address 가 만족되지 않는, inconsistency 문제가 발생한다.

→ Update Anomaly 발생.

이행 종속으로 인해 생긴 중복으로 2NF 를 만족함에도 여전히 Insert, Update, Delete 에서 Anomaly 가 존재한다. 따라서 이행 종속을 제거해야 하는 것이다.

그렇다면 이행 종속을 제거하기 위해 어떻게 해야 할까? 이를 위해 다시 한번 이행 종속이 생기는 이유를 이해 할 필요가 있다.

FD : user_id → city, city → address 가 relation user 에 같이 존재하기 때문에 user_id → address 가 Closure 에 의해 존재하게 되는 것.

따라서 이행 종속을 제거하기 위해서는 user(user_id, city), location(city, address) 로 decompose 할 필요가 있음을 알 수 있다.

1. user(user_id, city) 는 기존 FD : user_id → city 를 표현
2. location(city, address) 는 기존 FD : city → address 를 표현

(생각해보니 개념적으로 city —1:N—> address 인데 예제를 잘못 만든 것 같다.)

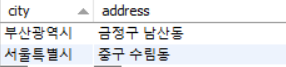
어쨋든, decompose 됨으로서 Trainsitive FD 를 제거해 3NF 를 만족시키고 Anomaly 를 제거 함을 확인 할 수 있다.

2NF 에서의 Anomaly 와 비교하면, FD : user_id → address 의 이행 종속이 제거되었으므로

1. FD : city → address 를 추가하는데 있어 insert anomaly 가 발생하지 않는다.

   → Insert Anomaly 제거

2. location relation 의 address 가 수정된다 해도 update anomaly 가 발생하지 않는다.

   → Modification Anomaly 제거

3. user relation 의 user_id : 2, 3 을 제거한다고 해서 '서울특별시' → '중구 수림동' 이라는 데이터가 제거되지 않으므로 delete anomaly 가 발생하지 않는다.

   → Delete Anomaly 제거

3NF 는 모든 Non Key Attribute 가 Primary Key 에 대해 Non transitive dependent 한 것을 요구한다. 이는 다시 말하면 Non Key attribute 들이 상호 독립적인 것이다.

Decomposition 에 대하여

1NF → 2NF → 3NF 로 normalization 하는 과정에서 모두 decomposition 을 적용하였음을 알 수 있다. 그렇다면 올바른 decomposition 은 어떻게 하는 걸까?

일단 위에서 이야기한대로 Partial FD 를 없에면서 Transitive FD 또한 없에는 방향으로 Decomposition 해야 하는 것은 당연하다.

그럼에도 추가적으로 고려해야 할 사항들을 알아두어야 한다.

1. 기존 Relation R 의 모든 FD 는 R1 과 R2 의 FD 에 대한 Logical Consequence

2. R1 과 R2 의 공통 attribute 는 R1, R2 둘 중 어느 한쪽에서 Candidate Key 이어야 한다.

3. Decompose 하는 것은 하는 건데 R 을 decompose 한 두 relation R1, R2 를 join 연산 할 경우 R 의 결과와 같아야 한다.

   → Non Loss join

위의 세가지 조건을 만족시키는 Decompose 의 경우 project 의 결과가 independent 하게 된다.

→ Dependency Preservation

BCNF (Boyce/Codd Normal Form) - Restircted 3NF

이전 3NF 를 만족한다면

1. row-and-column 의 값이 scalar 인 것
2. Partial FD 가 제거 됨
3. Transitive FD 가 제거됨

위의 3가지를 따를 것이다.

하지만 3NF 까지 normalization 하는 과정에서 relation R 이

1. candidate key 가 2개 이상인 경우
2. 각 candidate key 가 2개 이상의 attribute 로 구성되는 composite attribute 이며 candidate key 들의 attribute 가 overlapped 인 경우.

와 같은 경우를 추가적으로 고려하지 않았다.

BCNF 는 위에서 언급한 2가지 경우를 함께 normalization 한 것을 말한다.

즉, BCNF 는 모든 nontrivial, left-irreducible FD 에서 determinant 가 Candidate Key 인 것을 말한다.

→ BCNF 는 candidate Key 만이 오직 유일한 determinant 가 됨을 요구한다.

BCNF 로 normalization 하는 것이 어떤 Anomaly 를 해결 할 수 있는지 확인해보자.

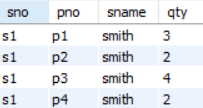
이 relation 은 overlapping candidate Key 를 가진다.

1. { sno, pno }
2. { sname, pno } - pno 가 overlapping 됨.

그런데 FD 가 다음과 같은데,

1. { sno, pno } → qty
2. { sname, pno } → qty
3. sno → sname
4. sname → sno

candidate key 가 아닌 sname 이 sno 를 determinant 함을 알 수 있다.

이로 인해 relation 에 redundancy 가 존재하게 되고 Update Anomaly 가 발생하게 된다.

1. Insert Anomaly

   FD : sname → sno 가 만족하므로 어떤 이름을 가지는 s 를 추가하기 위해서는 dummy pno 를 사용해야함.

2. Modification Anomaly

   sname 이 수정되면 sno 가 전부 수정되어야함.

3. Delete Anomaly

   sname 이 candidate key 가 아님에도 sname : smith 를 삭제하면 Lost Data 가 발생함.

여기서 redundancy 가 발생하는 이유는 명백히 FD : sname → sno, sno → sname 가 존재하기 때문이다. sname 이 candidate key 가 아님에도 determinate 할 수 있기 때문에 anomaly 가 생긴다.

이를 해결하기 위해서는 FD : sname → sno, sno → sname 의 FD 를 없에야 하는데 어떻게 할 수 있을까? (후보키가 아닌데 결정자의 역할을 하는 부분을 없애는게 핵심으로 이해했다.)

nontrivial FD : sname → sno, sno → sname 이 문제인 부분이므로 R 을 R1, R2 로 분해하되 R1(sno, sname) 으로, R2(sname, ...나머지) 를 적용한다.

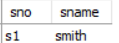
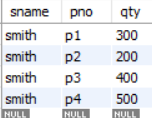
핵심은 기존에 candidate key 가 아니었던 sname 을 분해한 relation 에서 key 로 포함시키는 것이다.

이로 인해 결정자가 아닌데 결정자의 역할을 하는 FD 를 제거 할 수 있으므로 BCNF 를 만족 시키게 할 수 있다.

1. Partial FD 가 없는가?

   s 에는 당연히 없고 ssp 에는 { sname, pno } → qty 만 존재 하므로 만족, 1NF

2. Trainsitive FD 가 없는가?

   s 에는 당연히 없고 ssp 에서 sname → pno 가 아니므로 만족, 2NF