지난 장에서 HDD 등의 싸고 큰 메모리를 Memory Hierarchy의 맨 밑으로 추가해서 RAM 같은 메인 메모리가 부족할 때 Swap 영역이라는 곳에 값을 썼다가, 다시 필요할 때 읽는 식으로 마치 메모리가 더 있는 것처럼 사용할 수 있는 Demand paging에 대해 공부했다.
여기서 Swap in/out을 위한 Disk I/O Overhead가 매우 크기 때문에 물리 메모리가 부족해지면 어떤 페이지를 Swap out할지 결정하는 Replacement Policy를 잘 정하는 것이 매우 중요하다고 했는데, 이번 장에서는 좋은 Replacement Policy를 결정하기 위한 기준과 방법들에 대해 배울 것이다.
22.1. Cache Management
마치 메인 메모리와 캐시의 관계처럼, 접근하는데 걸리는 속도와 공간의 크기에 차이가 있다는 측면에서 HDD와 RAM도 비슷한 관계에 있다고 볼 수 있다. TLB에서 Miss가 발생할 때마다 메모리에 접근해야 하기 때문에 Miss ratio를 줄이는게 중요했던 것처럼, Swap에 있어서도 Page fault를 최소화하는 것이 이롭다.
지표가 있어야 각각의 Policy가 얼만큼 성능이 좋은지 평가할 수 있으므로 하나 정의해놓고 시작하자면, Cache Hit/Miss 비율을 고려해서 프로그램의 Acerage Memory Access Time(AMAT)를 아래와 같이 계산할 수 있다.
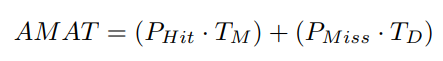
여기서 T_M은 메모리 액세스에 소요되는 시간, T_D는 디스크에 접근하는 시간을 의미하며, P_Hit와 P_Miss는 각각 Cache hit 비율과 Cache miss 비율을 의미한다. 비율을 의미하므로 P_Hit + P_Miss = 1.0이고, 각각의 P 값은 0 이상 1 이하의 값일 것이다.
T_M을 100ns, T_D를 10ms=10,000,000ns라 하면 P_Hit에 따른 AMAT는 아래와 같이 계산할 수 있다.
| P_Hit | P_Miss | AMAT |
|---|---|---|
| 0.5 | 0.5 | 5,000,050 ns |
| 0.9 | 0.1 | 1,000,090 ns |
| 0.99 | 0.01 | 100,099 ns |
| 0.999 | 0.001 | 10,099 ns |
| 0.9999 | 0.0001 | 1,099.99 ns |
| 0.99999 | 0.00001 | 200 ns |
차이가 눈에 보이는가! P_Hit가 그래서 이토록 중요한것이다.
22.2. The Optimal Replacement Policy
CPU Scheduling에서 STCF가 미래(여기서는 실행 종료까지 남은 시간)를 알고 있다는 가정하에 가장 이상적인, Optimal한 Policy이므로 이를 기준으로 다른 정책들의 성능을 평가했던 것처럼, Replacement Policy에서도 마찬가지로 기준이 될 Optimal한 정책이 필요하다.
그런데 그런게 있었으면 진작에 썼겠지? 미래에 있을 일들을 모두 알고 시스템을 준비한다는 것은 말도 안되기 때문에, STCF와 마찬가지로 이 절에서 배울 Optimal Replacement Policy(OPT) 역시 미래에 있을 일을 완전히 알고 있어야 하므로 실제로 구현할 수는 없다.
기본적인 아이디어는 간단한데, Belady라는 분에 의해 증명된대로 교체 시점으로부터 가장 나중에 접근될 페이지를 교체하는 것이 가장 적은 횟수의 Miss를 발생시키므로 최적임을 이용한다.
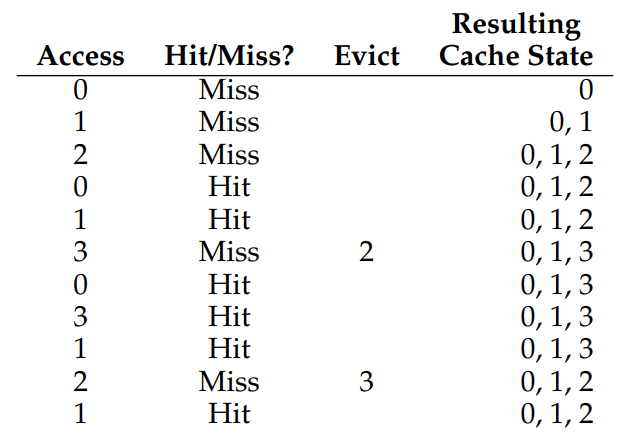
글로만 보면 잘 이해가 안되니까, 표를 놓고 생각해보자. 캐시가 3개의 페이지에 대한 정보를 저장할 수 있는 상태에서 순차적인 메모리 액세스에 따른 Cache hit 여부를 기록한 것이다.
맨 첫 0, 1, 2 페이지에 대한 액세스는 캐시에 아무 것도 없었으니 당연히 발생할 수 밖에 없는 Compulsory Miss(=Cold Miss)이고, 운좋게 그 다음 0, 1에 대한 액세스는 캐시에 0, 1이 있었으므로 Hit 되었다.
그 다음이 문제인데,, 이번엔 3번 페이지에 대한 액세스를 시도했으나 캐시에 값이 쓰여져 있지 않아 Cache Miss가 발생했고, 처리를 위해 캐시에 3번 페이지에 대한 정보를 삽입하려 했지만 이미 캐시의 모든 공간이 사용중이기 때문에 기존에 캐시에 남아 있던 정보 중 하나를 빼주어야 한다.
여기서 OPT 정책에 의하면, 해당 시점으로부터 가장~~ 마지막에 접근되는 페이지를 빼야 Miss가 최소로 발생하므로, 이후로 등장할 페이지 액세스 중 가장 먼 미래에 액세스 되는 페이지를 빼주면 된다.
| 페이지 | 몇 번 후에 접근? |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 4 |
보다시피 해당 시점으로부터 가장 나중에 접근되는 페이지가 2번 페이지이므로, 2번 페이지를 방출(Evict)하고 새로 들어온 3번 페이지를 캐시에 넣어준다.
다음으로 0, 3, 1, 2 순서의 페이지 접근이 발생했을 때 운좋게도 Cache hit가 발생했는데, 그 다음에 아까 빼놓은 2번 페이지에 대한 Miss가 또 발생했다!
그럼 이 시점으로부터 가장 먼 미래에 액세스 되는 페이지는 무엇인지 생각해보,, 려고 했는데, 어차피 1번 페이지에 대한 액세스밖에 남지 않았기 때문에 0과 3 중 아무거나 기계적으로 빼주면 된다. 이 경우에는 3이 빠지고 2가 다시 들어갔다.
여기서 Cache hit ratio를 따져보면, 총 11번의 접근 중 Cache hit가 6번, Miss가 5번이었으므로 약 54.5%의 Cache hit ratio를 보인다. 다만 Compulsory miss는 어떤 캐시이든 항상 발생할 수밖에 없기 때문에 맨 처음 발생한 3번의 Cache miss를 빼고 계산하면 총 85.7%. 꽤 높다!
그러나 말했듯 일반적인 상황에서는 앞으로 발생할 모든 미래(여기서는 페이지 액세스 순서)를 알 수 없기 때문에, 비교를 위해 고민해보았을 뿐 실제로 구현하여 사용할 수는 없다.
22.3. A Simple Policy: FIFO
CPU Virtualization에서 그랬듯, 먼저 들어온게 먼저 나가는 가장 간단한 FIFO(First In, First Out) 정책을 사용해 아까의 메모리 액세스 순서에 적용해보자.
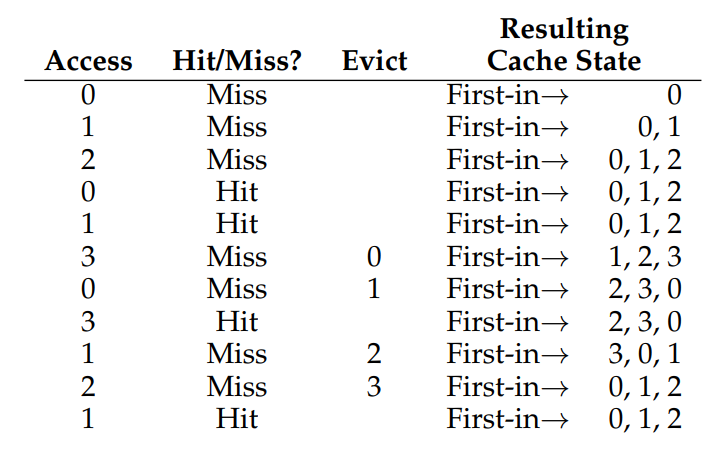
언뜻 보기에도 아까 공부한 OPT에 비해 처참하다.
맨 첫 3번까지의 Miss는 동일하게 Compulsory miss가 발생했으므로 제쳐 놓고, 이후에 Cache miss가 발생할 때마다 제일 오래 전에 들어온 페이지를 빼고 Miss가 발생한 새 페이지를 삽입하고 있다.
Cache hit ratio를 계산해보면, 11번 중 Compulsory miss를 제외하면 57.1%로 아주 박살이 났다. 탈락!
22.4. Another Simple Policy: Random
말 그대로 Cache miss가 발생할 때마다 랜덤하게 아무거나 골라서 내보내는 방식이다.
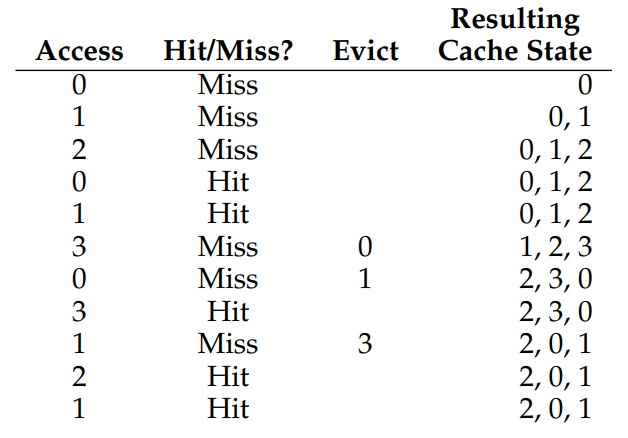
Cache hit ratio를 계산해보면 Compulsory miss를 제외하고 11번 중 3번의 Miss가 발생해 약 45.6%인데, Random Policy 특성상 의사 난수에 의지하기 때문에 Seed 값이 달라질 때마다 Cache hit ratio가 변하는 Unpredictable한 성질을 가진다. 따라서 Cache hit ratio가 0%가 될 수도, 100%가 될 수도 있다는 점!

위 그래프는 서로 다른 10000개의 Seed를 사용해 같은 메모리 액세스 순서에 적용했을 때 각각의 시행에서 Cache hit가 발생한 횟수별로 1씩 누적한 것인데, 보다시피 시행을 엄청나게 많이 했을 때 거의 OPT에 가까운 성능을 보이고 있음을 알 수 있다. 이러한 예외성 때문에 뒤에서도 종종 언급되니 눈여겨 봐두자.
22.5. Using History: LRU
FIFO와 Random 방식의 공통점은 무엇일까?
바로 Cache hit ratio를 높이기 위한 어떠한 노오오오력도 하지 않는다는 것이다. 예를 들어 FIFO에서 캐시 상태가 [0, 1, 2]인 상황에 페이지 3에 접근해서 캐시 상태가 [1, 2, 3]이 되었는데, 바로 다음에 페이지 0에 접근한다면? 좀 아깝지 않은가? Random은 그냥 무작위하게 내보낼 페이지를 고르기 때문에 아깝고 자시고 할 것도 없이 아무런 기대도 할 수 없다.
그럼 어떻게 Cache hit ratio를 높일 수 있는걸까?
미래에 일어날 일은 전혀 알 수 없으니 논외 대상이고, 방향을 돌려서 과거에 일어났던 일들을 참고해서 앞으로의 미래에 대비하는 방법이 좋을 것 같다. 미래는 알 수 없지만 적어도 이전에 많이 접근되었던 페이지라면 그렇지 않은 페이지보단 다음에 접근될 확률이 높을 테니까.
이걸 좀 더 구체적인 수치로 계량해보자면 Frequency와 Recency로 나눌 수 있는데, Frequency는 이전에 어떤 페이지가 여러 번 접근되었다면 다음에도 다시 접근될 확률이 높다는 의미이고, Recency는 최근에 접근된 페이지일수록 가까운 미래에 접근될 확률이 높다는 의미이다. (어디서 많이 본 것 같지 않은가? 특히 Recency는 TLB의 Temporal locality와 개념이 유사하다.)
코드로 예를 들자면 배열의 요소에 여러 번 접근하는 반복문이 이러한 Locality의 이점을 보는 사례라고 할 수 있는데, 앞에서부터 하나씩 접근하기 때문에 각각의 요소가 하나의 페이지 안에 붙어 있어 여러 번 접근될 것이고, 루프에 해당하는 코드 블럭을 처리할 때마다 페이지에 접근하며 다음 iteration에서도 또 접근할 것이기 때문이다.
이러한 아이디어가 녹아 있는 정책이 바로 Least Recently Used Policy, 즉 LRU이다.
이름부터 냄새가 솔솔 나는데, 그냥 최근에 가장 적은 빈도로 사용된 페이지를 내쫓는 정책이라 할 수 있다.
LRU는 마치 한 쪽이 불구덩이(?)로 연결되어 있는 컨베이어 벨트와 같다.
컨베이어 벨트를 캐시, 컨베이어 벨트 위에 올려지는 물건들을 페이지 정보라고 생각해보자. 이 컨베이어 벨트는 길이가 한정되어 있기 때문에(캐시의 크기) 정해진 수 이상의 물건을 올려 놓을 수 없으므로, 컨베이어 벨트가 옆으로 구를 때마다 맨 끝에 있던 가장 오래 전에 올려놓은 물건이 바닥으로 떨어지는 구조이다.
컨베이어는 그럼 언제 구르냐! 바로 새 물건을 올려 놓아야 할 때 구른다. 빈 자리가 나야 물건을 올려 놓을 수 있으니까(Replacement).
그런데 계속해서 쓰일 물건을 자꾸 바닥에 떨어뜨리면 다시 줍기 너무 귀찮지 않은가?(Overhead), 그래서 컨베이어 위에 있는 물건을 쓸 때마다 다시 컨베이어 벨트의 시작점(Most Recently Used, MRU)으로 옮겨 다시 맨 끝에 도달하기 전까지는 물건이 떨어지지 않도록 하면 편할 것이다. 별거 없고 이게 LRU다!
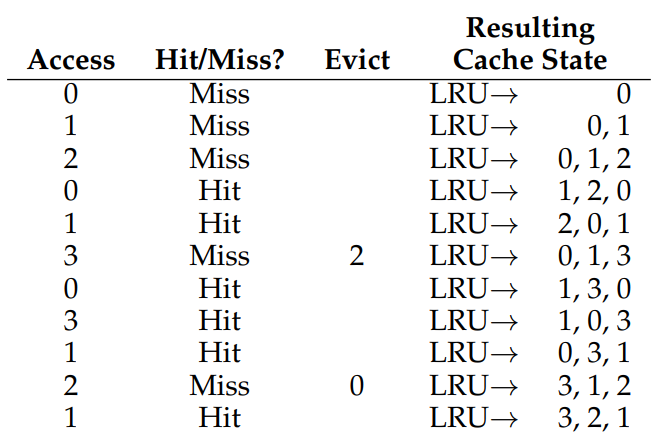
표로 다시 살펴보자. 0, 1, 2는 Cold miss로 동일한데, 그 다음 0번 페이지에 액세스하자 이전과 달리 Cache miss가 발생하지 않았는데도 Cache의 상태가 변했다!
맨 왼쪽을 가장 적은 빈도로 접근된 페이지(Least recently used)라고 하면, 0은 더이상 LRU가 아니므로 다시 컨베이어 벨트의 시작점으로 이동된 것이다. 그 다음의 1도 마찬가지로 더이상 LRU가 아니므로 같은 과정을 통해 다시 Cache의 끝(MRU)으로 이동되었다.
다음으로 3번 페이지에 접근하려 했으나 캐시에 값이 쓰여져 있지 않기 때문에 Cache miss가 발생했고, 3번 페이지를 캐시에 쓰기 위해 가장 오래전에 사용된 2번 페이지가 아래로 굴러떨어지고 3번 페이지가 캐시의 시작점으로 갔음을 확인할 수 있다. 이후 마지막 2번 페이지 액세스에서 발생한 Cache Miss에서도 마찬가지로 LRU였던 0이 굴러떨어지고, 2번 페이지가 캐시에 추가되었다.
Cache hit ratio는 놀랍게도 OPT와 동일한 85.7%로, FIFO와 Random 방식(Random의 경우 운이 나빴던 것이지만)에 비하면 매우 높은 수치이다.
Belady's Anomaly
LRU와 FIFO 사이의 성능 차이를 아까 OPT가 Cache hit ratio 측면에서 최적임을 증명했던 Belady 아저씨가 제시한 이상 현상으로 설명할 수 있다. 일반적으로 캐시의 크기를 늘리면 그만큼 성능이 좋아질 것 같은데, 그게 아니라 오히려 성능이 떨어질 수도 있다는 것인데, Random은 어차피 Unpredictable하므로 OPT, LRU, FIFO를 사용하되 캐시의 크기를 3개, 4개씩 주어 각각 두번씩 Cache hit ratio를 계산해보자.
(왼쪽은 Cache 크기가 3, 오른쪽은 Cache 크기가 4이다.)
OPT
| Access | Hit? | Evict | Cache after | Access | Hit? | Evict | Cache after | |
|---|---|---|---|---|---|---|---|---|
| 1 | Miss | [1] | 1 | Miss | [1] | |||
| 2 | Miss | [1, 2] | 2 | Miss | [1, 2] | |||
| 3 | Miss | [1, 2, 3] | 3 | Miss | [1, 2, 3] | |||
| 4 | Miss | 3 | [1, 2, 4] | 4 | Miss | [1, 2, 3, 4] | ||
| 1 | Hit | [1, 2, 4] | 1 | Hit | [1, 2, 3, 4] | |||
| 2 | Hit | [1, 2, 4] | 2 | Hit | [1, 2, 3, 4] | |||
| 5 | Miss | 4 | [1, 2, 5] | 5 | Miss | 4 | [1, 2, 3, 5] | |
| 1 | Hit | [1, 2, 5] | 1 | Hit | [1, 2, 3, 5] | |||
| 2 | Hit | [1, 2, 5] | 2 | Hit | [1, 2, 3, 5] | |||
| 3 | Miss | 2 | [1, 5, 3] | 3 | Hit | [1, 2, 3, 5] | ||
| 4 | Miss | 3 | [1, 5, 4] | 4 | Miss | 3 | [1, 2, 5, 4] | |
| 5 | Hit | [1, 5, 4] | 5 | Hit | [1, 2, 5, 4] |
Cache 크기가 3일 때는 5/12, 4일 때는 6/12로 캐시 크기가 늘어남에 따라 Cache hit ratio도 상승했다.
FIFO
| Access | Hit? | Evict | Cache after | Access | Hit? | Evict | Cache after | |
|---|---|---|---|---|---|---|---|---|
| 1 | Miss | [1] | 1 | Miss | [1] | |||
| 2 | Miss | [1, 2] | 2 | Miss | [1, 2] | |||
| 3 | Miss | [1, 2, 3] | 3 | Miss | [1, 2, 3] | |||
| 4 | Miss | 1 | [2, 3, 4] | 4 | Miss | [1, 2, 3, 4] | ||
| 1 | Miss | 2 | [3, 4, 1] | 1 | Hit | [1, 2, 3, 4] | ||
| 2 | Miss | 3 | [4, 1, 2] | 2 | Hit | [1, 2, 3, 4] | ||
| 5 | Miss | 4 | [1, 2, 5] | 5 | Miss | 1 | [2, 3, 4, 5] | |
| 1 | Hit | [1, 2, 5] | 1 | Miss | 2 | [3, 4, 5, 1] | ||
| 2 | Hit | [1, 2, 5] | 2 | Miss | 3 | [4, 5, 1, 2] | ||
| 3 | Miss | 1 | [2, 5, 3] | 3 | Miss | 4 | [5, 1, 2, 3] | |
| 4 | Miss | 2 | [5, 3, 4] | 4 | Miss | 5 | [1, 2, 3, 4] | |
| 5 | Hit | [5, 3, 4] | 5 | Miss | 1 | [2, 3, 4, 5] |
Cache 크기가 3일 때는 3/12였는데, 4일 때는 안그래도 나빴던 Cache hit ratio가 2/12로 감소했다.
OPT야 말 그대로 Optimal이니까 그렇다 치는데, LRU는 그럼 어떨까? FIFO만 이렇게 된걸까?
LRU
| Access | Hit? | Evict | Cache after | Access | Hit? | Evict | Cache after | |
|---|---|---|---|---|---|---|---|---|
| 1 | Miss | [1] | 1 | Miss | [1] | |||
| 2 | Miss | [1, 2] | 2 | Miss | [1, 2] | |||
| 3 | Miss | [1, 2, 3] | 3 | Miss | [1, 2, 3] | |||
| 4 | Miss | 1 | [2, 3, 4] | 4 | Miss | [1, 2, 3, 4] | ||
| 1 | Miss | 2 | [3, 4,1] | 1 | Hit | [2, 3, 4, 1] | ||
| 2 | Miss | 3 | [4, 1, 2] | 2 | Hit | [3, 4, 1, 2] | ||
| 5 | Miss | 4 | [1, 2, 5] | 5 | Miss | 3 | [4, 1, 2, 5] | |
| 1 | Hit | [2, 5, 1] | 1 | Hit | [4, 2, 5, 1] | |||
| 2 | Hit | [5, 1, 2] | 2 | Hit | [4, 5, 1, 2] | |||
| 3 | Miss | 5 | [1, 2, 3] | 3 | Miss | 4 | [5, 1, 2, 3] | |
| 4 | Miss | 1 | [2, 3, 4] | 4 | Miss | 5 | [1, 2, 3, 4] | |
| 5 | Miss | 2 | [3, 4, 5] | 5 | Miss | 1 | [2, 3, 4, 5] |
Cache 크기가 3일 때는 2/12였는데, 4일 때는 4/12로 2배 가량 증가했다.
Stack Property
보다시피 FIFO를 제외한 OPT, LRU의 경우 캐시 크기를 늘리자 Cache hit ratio가 증가했는데, FIFO만은 오히려 성능이 나빠졌다.
이는 우연이 아니라 Stack Property에 의한 결과인데, LIFO 같은 성질을 얘기하는게 아니라 캐시 크기가 N일 때 어떤 시점에 캐시 안에 들어 있던 요소들이 캐시 크기를 N+1로 키웠을 때 그대로 다 들어 있는 성질을 의미한다.
OPT, LRU는 Stack property를 가지는 반면, FIFO에는 Stack property가 없어 이러한 결과가 나타난 것이다. Cache 크기를 키워봤자 이전에 가지고 있던 요소를 그대로 보존하고 있는게 아니니까 같은 상황에서 Cache 크기를 늘리는게 의미가 없을 뿐더러 심지어 성능에 악영향을 끼칠 수도 있는 이 현상을 Belady's Anomaly라 한다.
22.6. Workload Exmples
OPT, FIFO, Random, LRU 방식으로 교체할 페이지를 고르는 과정을 살펴보았으니, 여러 상황(workload)에서 각각의 Policy를 적용했을 때의 Cache hit ratio를 살펴보자.
아래 등장하는 모든 그래프는 100개의 페이지에 10000번 접근하는 상황에서의 Cache hit ratio를 측정한 것이라고 한다.
No-Locality Workload
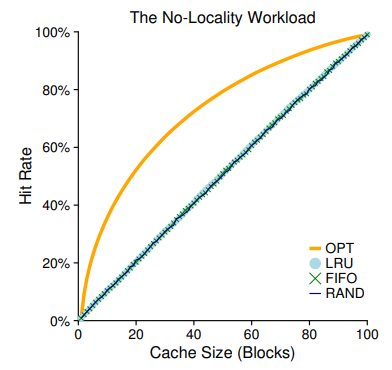
Locality가 아~~예 없는 상황에서 각각의 Policy들의 성능을 비교한 것이다.
Locality가 아예 없다는건 그냥 여기저기 껑충껑충 페이지를 참조하고 다닌다는 의미인데, 다음에 나오는 그래프도 그렇겠지만 페이지 갯수가 100개인데 캐시에도 100개의 페이지를 저장할 수 있으면 당연히 Compulsury miss를 제외하곤 Hit rate가 100%가 된다는 점도 잘 눈여겨 봐두자.
여하튼 어떤 상황에서도 최적임이 보장되는 OPT를 제외하면, LRU, FIFO, RAND 모두 Cache 크기에 비례하여 성능이 향상됨을 확인할 수 있다.
위에서 Belady's Anomaly에 의해 FIFO가 Cache size가 증가해도 성능에 영향이 없거나 오히려 악영향을 끼친다고 했는데, 여기서는 LRU 역시 Locality의 이점을 사용할 수 없는 무작위 액세스이기 때문에 비슷한 성능이 나온 것이다.
Random 방식의 결과도 좀 특이한데, 시행을 여러 번 하다보니 평균적으로 FIFO와 LRU의 성능에 근접한 모습을 확인할 수 있다.
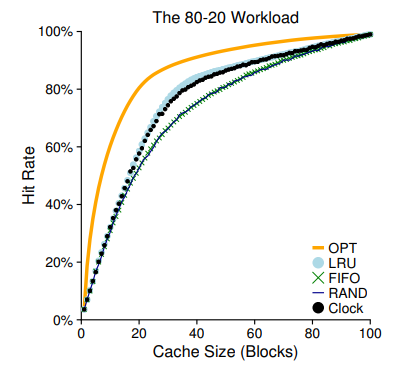
The 80-20 Workload
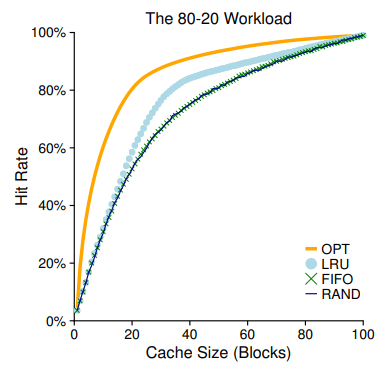
80-20 Workload는 일반적인 상황에서의 Locality를 대변한다고 할 수 있는데, 보통 프로세스에서 사용되는 20%의 인기 있는 페이지에 대한 접근이 전체 페이지 액세스의 80%만큼을 차지하고, 그렇지 않은 나머지 80%의 인기 없는 페이지에 대한 접근은 전체 페이지 액세스의 20%만큼을 차지하기 떄문이라고 한다. 될놈될,, 안될안,,,,
여하튼 OPT는 당연히 가장 높은 성능 증가율을 보이고 있고, LRU도 Locality의 이점을 얻어 꽤 선방하고 있다.
공동 꼴찌는 FIFO와 RAND이다. 하나는 Stack Property가 없고, 다른 하나는 Unpredictable하므로, 탈락! 일 것 같지?
The Looping-Sequential Workload
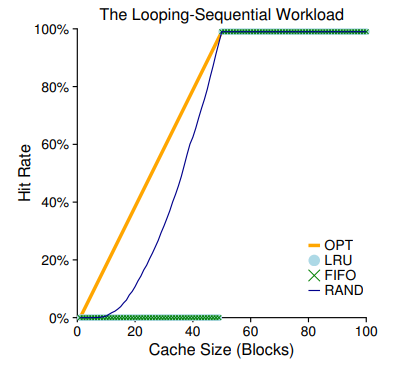
여기서는 50개의 페이지들을 순차적으로 접근하는데, 예를 들어 0번 페이지부터 50번 페이지까지 접근한 다음 또 다시 0번 페이지부터 49번까지 접근하는 것을 총 10000 / 50 = 200번 반복한다는 의미이다.
가장 눈여겨봐야 할 Workload이므로 Policy를 하나씩 뜯어보자.
OPT
캐시 크기가 전체 페이지 크기의 절반에 이르기 전까지는 선형적으로 Hit ratio가 증가하는데, 절반을 지난 이후로는 100%의 Hit rate를 보이고 있다.
지역성을 가장 잘 활용하고 있는 것인데, Cache 크기가 50에 도달하기 전까지는 앞으로의 메모리 액세스 스케줄을 전부 알고 있기 때문에 Cache 크기가 1씩 증가할 때마다 미래에 한 번씩 더 대비할 수 있는 셈이다.
Cache 크기가 49인 상황에서는 아래와 같이 작동할 것이다.
| Access | Hit? | Evict | Cache after |
|---|---|---|---|
| 0 | Miss | [0] | |
| 1 | Miss | [0, 1] | |
| ... | ... | ... | ... |
| 48 | Miss | [0, ... , 48] | |
| 49 | Miss | 48 | [0, ... , 47, 49] |
| 0 | Hit | [0, ... , 47, 49] | |
| 1 | Hit | [0, ... , 47, 49] | |
| ... | ... | ... | ... |
| 47 | Hit | [0, ... , 47, 49] | |
| 48 | Miss | 47 | [0, ... , 46, 48, 49] |
| 49 | Hit | [0, ... , 46, 48, 49] | |
| 0 | Hit | [0, ... , 46, 49, 50] | |
| ... | ... | ... | ... |
이런식으로!
크기가 49일 때는 잘 와닿지 않을 수 있는데, Cache 크기가 50이면 아래와 같이 작동할 것이다.
| Access | Hit? | Evict | Cache after |
|---|---|---|---|
| 0 | Miss | [0] | |
| 1 | Miss | [0, 1] | |
| ... | ... | ... | ... |
| 49 | Miss | [0, ... , 49] | |
| 0 | Hit | [0, ... , 49] | |
| 1 | Hit | [0, ... , 49] | |
| ... | ... | ... | ... |
| 47 | Hit | [0, ... , 49] | |
| 48 | Hit | [0, ... , 49] | |
| 49 | Hit | [0, ... , 49] | |
| 0 | Hit | [0, ... , 49] | |
| ... | ... | ... | ... |
최초에 발생하는 50회의 Cold miss를 제외하면, 모두 Cache hit이므로 Cache hit ratio가 100%인 것이다!
이것은 다른 Policy에서도 동일한데, 어차피 접근되는 페이지가 50가지 밖에 없기 때문에 딱 배열 갯수 만큼의 페이지만 캐시 크기가 충족되면 Cache miss가 발생할 일이 없기 때문이다.
FIFO
Cache 크기가 49인 상황에서는 아래와 같이 작동한다.
| Access | Hit? | Evict | Cache after |
|---|---|---|---|
| 0 | Miss | [0, 1, 2] | |
| 1 | Miss | [0, 1, 2] | |
| 2 | Miss | [0, 1, 2] | |
| ... | ... | ... | ... |
| 48 | Miss | [0, ... , 48] | |
| 49 | Miss | 0 | [1, ... , 49] |
| 0 | Miss | 1 | [2, ... , 49] |
| ... | ... | ... | ... |
위와 같이 맨 처음 발생하는 Cold Miss를 기껏 다 견뎌도, Cache의 크기 자체가 작아 사용하기 직전에 페이지가 캐시로부터 쫓겨나고 있음을 확인할 수 있다.
Cache 크기를 50으로 늘리면 어떨까?
| Access | Hit? | Evict | Cache after |
|---|---|---|---|
| 0 | Miss | [0, 1, 2] | |
| 1 | Miss | [0, 1, 2] | |
| 2 | Miss | [0, 1, 2] | |
| ... | ... | ... | ... |
| 49 | Miss | [0, ... , 49] | |
| 0 | Hit | [0, ... , 49] | |
| 1 | Hit | [0, ... , 49] | |
| ... | ... | ... | ... |
Cache 크기가 50을 넘자, OPT와 마찬가지로 Cache hit ratio가 100%가 되었음을 확인할 수 있다.
LRU
LRU 역시 캐시의 크기 자체가 모자라면 Loop-Sequential Workload에서 맥을 못추린다.
Cache 크기가 49일 때 다음과 같이 작동한다.
| Access | Hit? | Evict | Cache after |
|---|---|---|---|
| 0 | Miss | [0, 1, 2] | |
| 1 | Miss | [0, 1, 2] | |
| 2 | Miss | [0, 1, 2] | |
| ... | ... | ... | ... |
| 48 | Miss | [0, ... , 48] | |
| 49 | Miss | 0 | [1, ... , 49] |
| 0 | Miss | 1 | [2, ... , 49] |
| ... | ... | ... | ... |
FIFO와 같은 이유로 정확히 동일하게 작동하는데, Cache 크기가 50일 때에도 동일하다.
| Access | Hit? | Evict | Cache after |
|---|---|---|---|
| 0 | Miss | [0, 1, 2] | |
| 1 | Miss | [0, 1, 2] | |
| 2 | Miss | [0, 1, 2] | |
| ... | ... | ... | ... |
| 49 | Miss | [0, ... , 49] | |
| 0 | Hit | [0, ... , 49] | |
| 1 | Hit | [0, ... , 49] | |
| ... | ... | ... | ... |
Random
Random이 좀 특이한데, Cache 크기가 50을 넘으면 당연히 교체가 발생하지 않기 때문에 Cache hit ratio가 100%인건 둘째치고 OPT보단 못하지만 그래도 캐시 크기가 증가함에 따라 꾸준히 증가하고 있다. Locality를 활용하던 LRU가 캐시 사이즈를 일정 이상 충족하지 못하면 Hit ratio가 0%인 것에 비하면 이는 아주 놀라운 수치이다!
22.7. Implementing Historical Algorithm
물론 LRU가 Loop-Sequential Workload에서 맥을 못추기는 하지만, 그래도 Unpredictable한 Random 방식이나 아무런 노력도 하지 않는 무지성 FIFO보다는 훨씬 낫다.
근데 이게 눈으로 쫓아가는건 금방 해서 잘 티가 안나는데, 컴퓨터 입장에서는 매 페이지 액세스마다 어떤 페이지가 MRU인지, LRU인지 알고 있어야 Cache Hit가 발생했을 때 해당 페이지를 MRU로 밀어 넣어주고, Cache miss가 발생했을 때 LRU에 있던 값을 내보내줄 수 있다. 이걸 매 액세스마다 O(N)쯤의 시간 복잡도로 수행한다면,, 비용이 어마어마하게 많이 들 것이다.
그렇기 때문에 페이지 접근이 있을 때마다 메모리의 마지막 접근 시간을 기록해놓고 교체가 필요할 때 가장 오래된 페이지를 내쫓는 방법을 HW를 통해 지원 받을 수 있기는 한데, 이것도 마찬가지로 '가장' 오래된 페이지를 찾아야 하기 때문에 약간 더 나아질 뿐 여전히 비현실적인 성능이다.
22.8. Approximating LRU
이렇듯 LRU는 구현하기 어렵지만, LRU에 근사하도록 구현할 수는 있다.
가장 오래된 페이지를 고르는건 비용이 많이 들지만, 그냥 아주 최근에만 접근된게 아니라 적당히 오래된 것들 중에서 골라도 어느정도는 LRU의 성능에 근사하게 설계할 수 있다.
이를 표시하기 위해 use bit라는 일종의 flag를 사용할 수 있는데, 간단하게 페이지가 참조될 때마다 HW가 이 값을 1로 전환하고, 0으로 전환하는 것은 HW가 아닌 OS에 내장된 어떤 규칙에 의해 수행되어 해당 캐싱 정보가 '오래된' 것임을 나타내는 것이다.
그럼 OS는 어떤 규칙을 통해 use bit를 0으로 전환하는 걸까?
여러 방법이 있지만 가장 간단한 알고리즘은 Clock Algorithm이다. 위에서 HW의 지원을 받아 각각의 페이지가 마지막으로 참조된 시각을 기록해서 Clock이 아니라, 자료 구조가 원형 연결 리스트로 구성되어 마치 시계처럼 생겼기 때문이다. (강의 자료에 어떻게 생겼는지 나와 있기는 한데, 시간도 없고 귀찮아서(...) 그냥 글로만 적어 놓겠다. 나중에 이 글을 다시 찾아볼 나, 구글 드라이브로 가서 찾아봐라,,)
마치 시계바늘이 숫자를 가리키듯, 원형 연결 리스트의 어떤 노드를 가리키고 있다고 생각해보자.
페이지를 교체해야 할 때마다 OS는 이 바늘이 가리키고 있는 페이지의 use bit를 확인해서 0인 경우 해당 노드에 새 페이지 정보를 기록하고 바늘을 한 칸 뒤로 옮긴다.
1인 경우 사용중인 페이지이므로 교체하지 않고 넘기되, use bit를 0으로 전환해 다시 한 바퀴 돌아 바늘이 이 페이지를 가리킬 때까지 1로 바뀌어 있지 않으면 페이지가 교체된다.
use bit를 확인해서 0인 경우 데이터를 새로 써주고 바늘을 한 칸 만큼 뒤로 옮기는게 기억이 잘 안 날 수 있는데, 방금 캐싱된 노드 입장에서는 캐싱되자마자 바로 교체되면 좀 억울하니까, 다시 바늘을 받을 때까지 시간을 좀 넉넉하게 준 것이라고 생각하자.
만약 교체를 하기는 해야 하는데 모든 노드의 use bit가 1이라면?
이때는 어쩔 수 없이 바늘이 처음 가리키던 노드부터 끝 노드까지 쭉 돌면서 0으로 만들어주다가, 바늘이 처음 가리킨 노드에 도착해 use bit가 0임을 확인하고 이 위치에 새 데이터를 써준 뒤 마찬가지로 바늘을 한 칸 뒤로 옮기면 된다.
이렇게 모든 페이지의 use bit가 1이면 한바퀴를 무조건 돌아야 하기 때문에, 차례대로 use bit를 검사하는게 아니라 임의로 아무 페이지나 골라서 해당 페이지의 use bit가 1이면 0으로 전환하고 패스, 0이면 해당 페이지에 새 데이터를 써주는 식의 응용 알고리즘도 있다.
이게 생각보다 성능이 나쁘지 않은지, 아까 살펴본 80-20 Workload에서 거의 LRU에 근접한 성능을 보여주고 있다.
22.9. Considering Dirty Pages
18장에서 Dirty bit에 대해 아래와 같이 설명했었다.
- Dirty Bit
위의 Present bit의 연장선상에 있는 비트인데, 해당 프레임의 데이터가 메모리에 올라온 이후에 내용이 변경되었는지를 표시하기 위한 비트이다. 만약 내용이 변경되지 않았다면 굳이 디스크에 값을 덮어쓸 필요 없이 언제든 그냥 메모리에 데이터를 올려서 쓸 수 있겠지만, 메모리에서 값이 변경되었다면 디스크에도 이 내용을 반영해주어야 하기 때문에 필요하다. (마찬가지로 나중에 이해해도 된다.)
..이제 이해할 때가 되었다!
당연히 캐시의 값이 변경되었으면 교체시 캐시 데이터를 그냥 삭제해버리는게 아니라 디스크에 다시 써주는 작업이 필요한데, 이것 역시 I/O이기 때문에 CPU 사용률에 악영향을 끼친다.
따라서 만약 use bit가 둘 다 0인데 한쪽은 dirty bit가 1, 다른쪽은 0이라면 I/O가 필요 없는 Dirty bit 0쪽을 선택해 캐시에서 삭제해주는게 훨씬 저렴하므로 알고리즘에 이를 반영하여 성능을 향상시킬 수 있다.
22.10. Other VM Policies
말고도 성능 향상을 위해 이런 저런 방법들을 도입할 수 있다.
예를 들자면 저번 장에서 슬쩍 언급했듯이 OS가 보기에 어떤 페이지가 곧 사용될 것 같다! 싶으면 미리 메모리에 읽어 들이는 Prefetching이라던지(Spatial locality를 기대하고 한 번에 근처에 있는 데이터들을 미리 캐싱해놓는 등), Disk I/O가 필요한 페이지들을 하나씩 swap out하는게 아니라 모아뒀다가 한 번에 하는 Clustering 같은 방법들이 있다.
22.11. Thrashing
만약 물리 메모리는 턱없이 부족한데 사용하려는 프로세스만 많다면 어떻게 될까?
메인 메모리에 비해 HDD에 위치해 있는 Swap 영역은 충분히 넓기 때문에 사용하려면 사용할 수야 있겠지만, 계속해서 Swapping이 발생해야 한다. 이런 Swapping 작업들 자체가 비용이 굉장히 많이 들어가기 때문에, 여기에 따로 Thrashing이라 이름을 붙여 대응한다.
이걸 좀 정량화해서 표현하자면 특정 단위 시간 동안 사용되는 페이지들의 집합을 Working set이라 하는데, 각각의 Working set에 포함된 페이지 갯수가 메모리에서 무리 없이 제어할 수 있는 프로세스의 수보다 커질 경우 Thrashing이 발생한다고 할 수 있다.
Thrashing을 해결하기 위한 몇 가지 방법들이 있는데, 초기 운영체제에선 실행되는 프로세스 수를 아예 줄인 다음 메인 메모리가 어느정도 감당할 수 있을 정도만 남겨 놓고 운영하는 Admission Control 기법이라던지, 좀 무책임하긴 하지만 무리가 간다 싶으면 메모리를 많이 잡아먹는 프로세스를 그냥 냅다 죽여버리는 방법도 있다고 한다.
마무리
Page replacement에도 비용이 들어가기 때문에 교체할 페이지를 현명하게 고르는 여러 정책들에 대해 공부해 보았다. 강의때 다뤄 주신 내용이 중간중간 누락되었는데, 그건 기회가 되면 천천히 채워 넣겠다. 일단 시험공부부터 빡시게 해보고,,
여하튼 이를 끝으로 드디어 Memory Virtualization까지 끝냈다. 이제 중간 시험 보고, 한 일주일 쉰 다음 천천히 다시 돌아와야겠다.
내 생각엔 딱 강의 진도랑 일주일정도 차이나는게 딱 좋은 것 같으니, 시험 기간에 몰아서 하지 말고 시험 끝나면 좀 쉬다가 바로 포스팅할 수 있도록 노력해봐야겠다.
고생했다! 나!

