Link to Paper:
“Inverted Residuals and Linear Bottlenecks” -2019
— Mark Sandler, Andrew Howard, Menglong Zhu, Andrey Zhmoginov, Liang-Chieh Chen - Google Inc.
https://arxiv.org/pdf/1801.04381
Table of Contents
- Introduction
- Depthwise Separable Convolutions
- Linear Bottlenecks
- Inverted Residuals
- Model Architecture
- Code
- Experiment
1. Introduction
MobileNetV1과 마찬가지로 모바일 장치나 임베디드 시스템과 같이 자원이 한정적인 상황에서 성능을 유지하면서 경량화된 모델을 설계하는 방법으로 기존 방법인 Depthwise Separable Convolution에 추가적으로 ResNets의 Residual Block의 잔차연결을 Inverted(반전된) 구조로 학습하여 기존 MobileNetV1 보다 효율적인 성능을 보여줍니다.
2. Depthwise Separable Convolutions
Depthwise Separable Convolutions 기법은 합성곱을 깊이 별 합성곱과 1X1 합성곱으로 나누는 형태의 Factorized Convolution
즉, 합성곱의 연산과정을 2단계로 분해하는 방법
이 과정으로 연산 비용을 감소효과를 가져옴
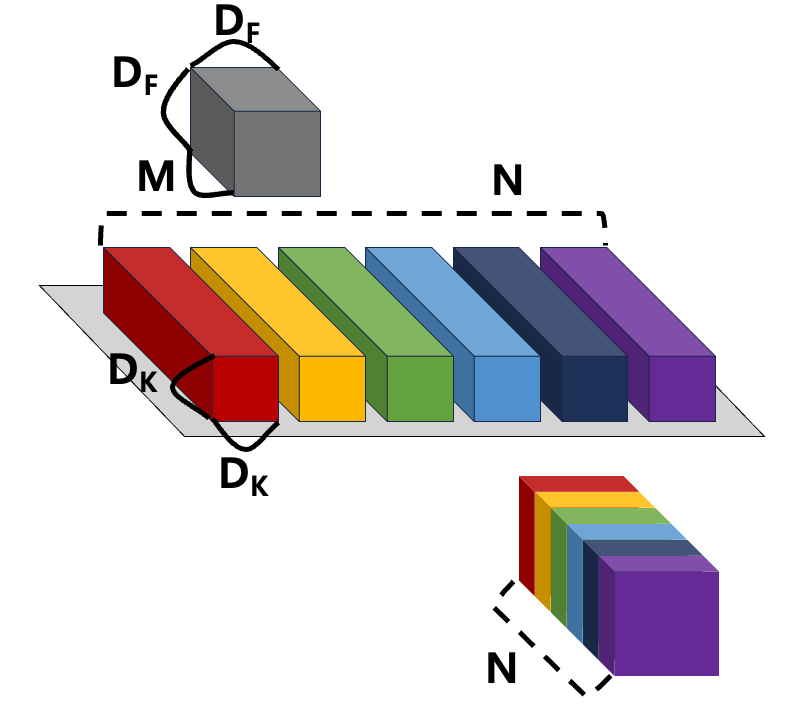
fig.1
fig.1을 기준으로 in_feature 의 shape는[]
Conv Layer의 커널 사이즈 [], 개 로 정의 했을 때, 그 수식은
논문에서는, 기존 연산 과정을 Depth wise(공간 축), Point wise(채널 축) 으로 나눠서 계산
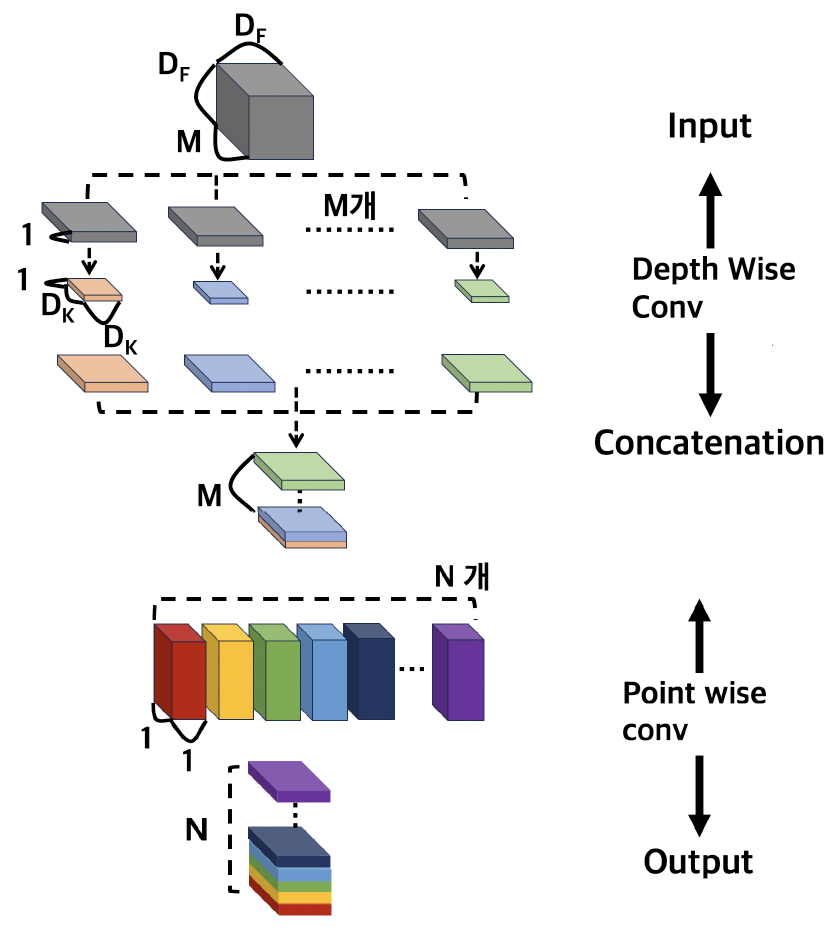
fig.2
fig.2 처럼 기존 연산 과정을 나눠서 계산
Input → Separate → Depth Wise Conv → Concat → Point wise Conv → Output
의 형태로 계산
Depth Wise Conv(공간 축) 는
Cost를 계산할 수 있으며,
Point wise Conv(채널 축)는 계산된다.
결과적으로 기존 Conv 계산 방식에 비해 Depth Wise Conv + Point Wise Conv의 계산 방식은 다음과 같이 계산량이 감소 하는데,
이러한 감소량을 보인다.
예시로,
32 X 32 X 3 ( 이미지 크기: 32X32, 채널 수: 3)
3 X 3 (커널 크기)
64 (출력 채널 수)
계산량 =
Depthwise Separable Convolution
결과적으로 계산량은 다음과 같다,
2.1 Width Multiplier(α)
MobileNet의 모델의 ‘채널 수’ 를 조정하여 네트워크 크기와 계산 비용을 조절한다.
네트워크의 Width에 해당하는 채널 개수가 조절 되어서, 모델의 경량화 효과를 줄 수 있다.
논문에서는 α 의 범위를 1-0 사이 값으로 정했으며, 실험으로는 1, 0.75, 0.5, 0.25로 사용 되었다.
연산 Cost 는 다음과 같이 조절된다.
2.3 Resolution Multiplier(ρ)
MobileNet의 모델의 ‘이미지 크기’를 조절하여 네트워크 크기와 계산 비용을 조절한다.
논문에서는 ρ 의 범위를 1-0 사이 값으로 정했으며, 계산으로 Input 이미지를 224, 192, 160, 128로 조정하여 사용 되었다.
연산 Cost는 다음과 같이 조절된다.
3. Linear Bottlenecks
Manifold 가설을 통한 Linear Bottlenecks의 필요성
3.1 Manifold
Neural Network에서는 중요한 Manifold가 하위 차원에 임베디드될 수 있다는 가정을 해왔습니다.
즉, 정보들이 고차원 공간에 퍼져 있지 않고, 저차원 공간에 위치할 수 있다라는 가정입니다.
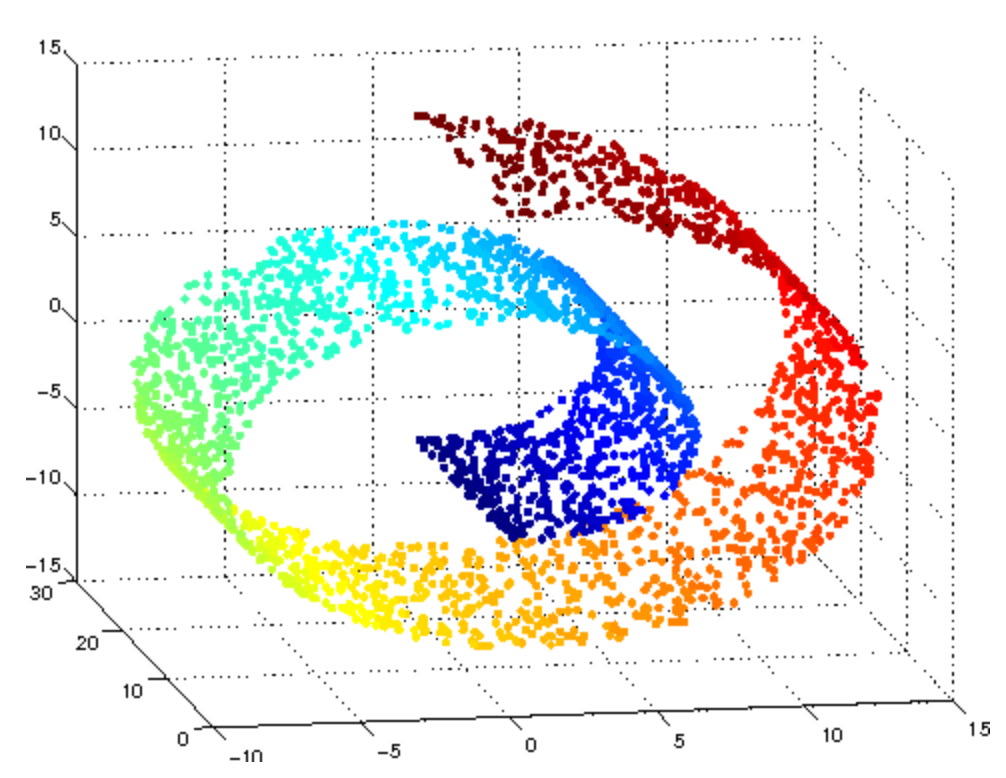
가장 보편적으로 Manifold를 설명할 때 나오는 스위스롤을 예시로 보면,
그 롤 위에 개미가 있고 롤 안쪽부터 바깥쪽의 거리를 개미가 비유클리디안 형태를 만져가며 모양을 이해해 나가는 것을 생각하면 이해하기 쉬울 것이다. 즉, 스위스롤도 신경망 모델 입장에서 경우에 따라 말린 부분을 펼친 모양으로 나타낼 수 있다는 말이다.
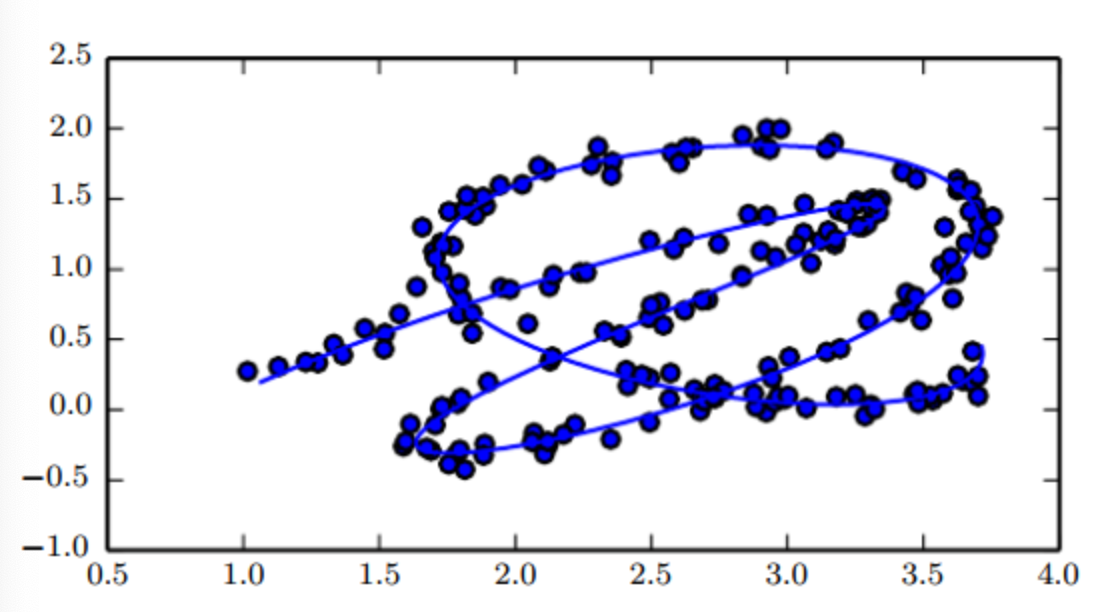
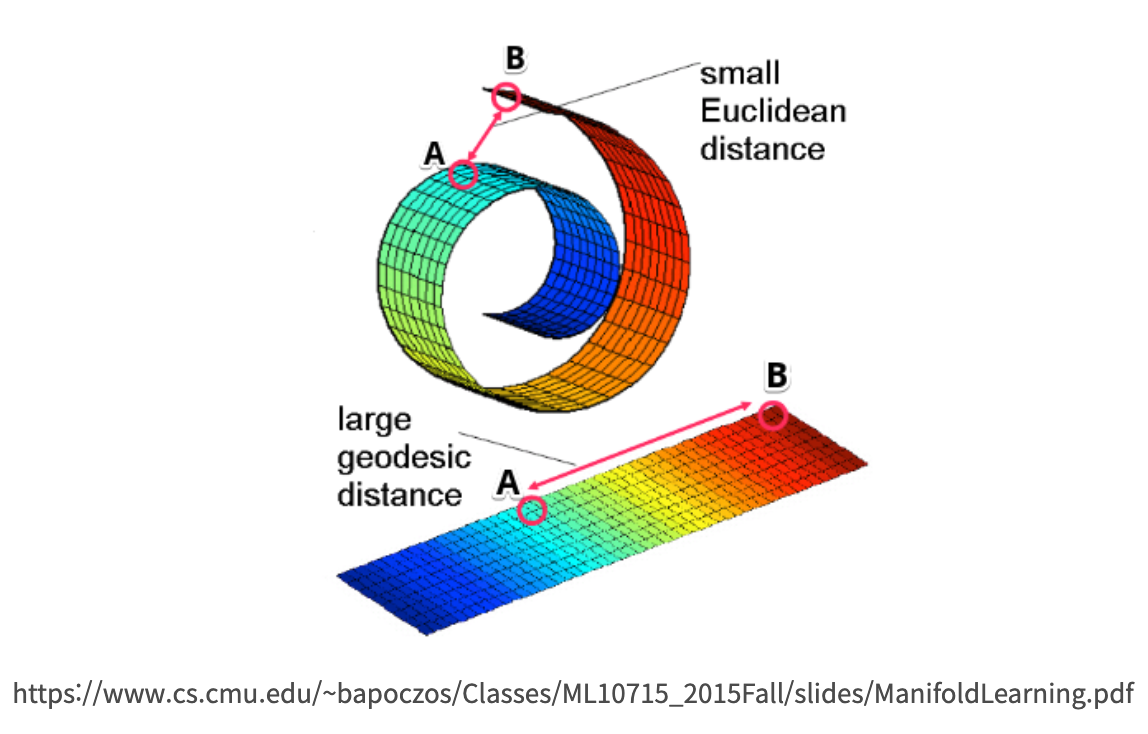
데이터 A와 데이터 B 사이를 보간(Interpolation)하면, 3차원 상의 A↔B 보간하는 것 보다, 2차원의 매니폴드 상의 A↔B를 보간하는 것이 해당 데이터에 더 적절한 방법이다 라는 가정.
MNIST 데이터에 대하여 2~0 사이를 보간하는 내용을 예시로,
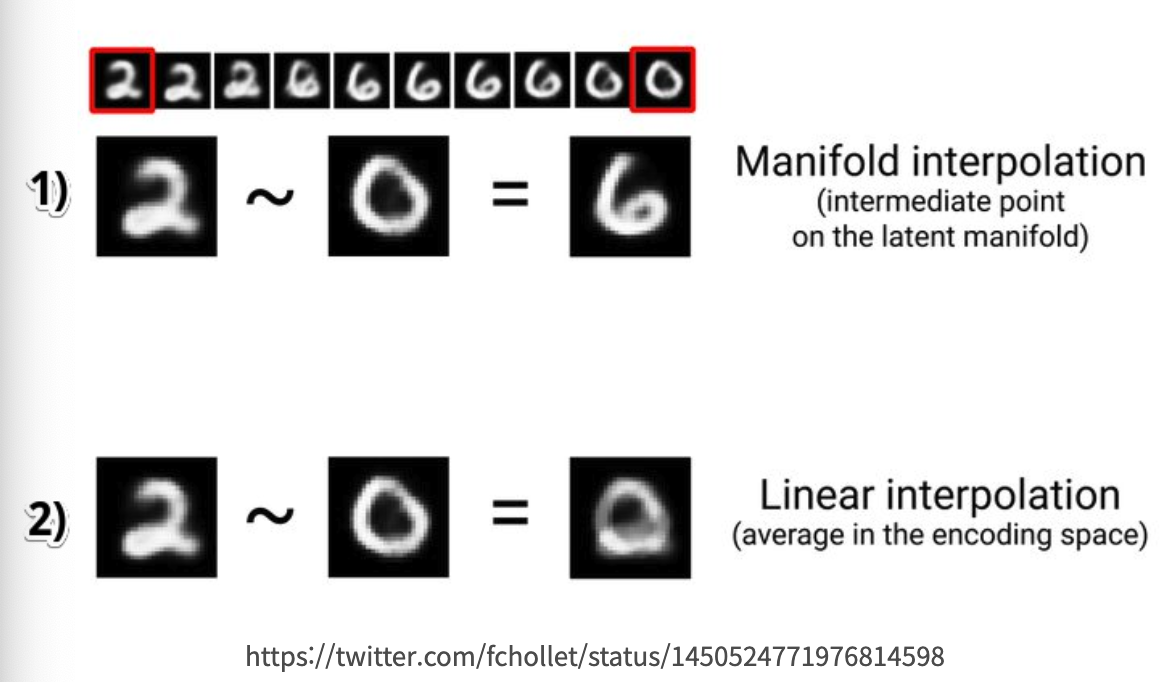
1) Manifold Interpolation(매니폴드 보간) : 2에 대한 데이터, 0에 대한 데이터 사이에 6에 대한 데이터가 존재한다고 볼 수 있다.
2) Linear Interpolation(선형 보간) : 픽셀 값의 평균을 사용하여 보간하면(Linear Interpolation)을 하면 명확한 숫자가 나오지 않아 적절하게 보간되지 않았음을 볼 수 있다.
이 일련의 과정을 통해서,
저차원에 있다는 가설을 바탕으로, 치원을 줄여도 정보 손실이 없이 데이터를 압축이 가능하다 라는 직관이 생기게 된다. 즉, 입력 이미지가 텐서로 변환되는 각 컨볼루션 연산을 통해 차원이 줄어드는 부분으로 생각 하면 된다.
이러한 직관은,
MobileNetV2에서는 BottleNeck(Linear BottleNeck)구조를 이용하여 계산비용 및 메모리 사용을 줄이면서 성능을 유지했다.
3.2 ReLU의 비선형성 문제
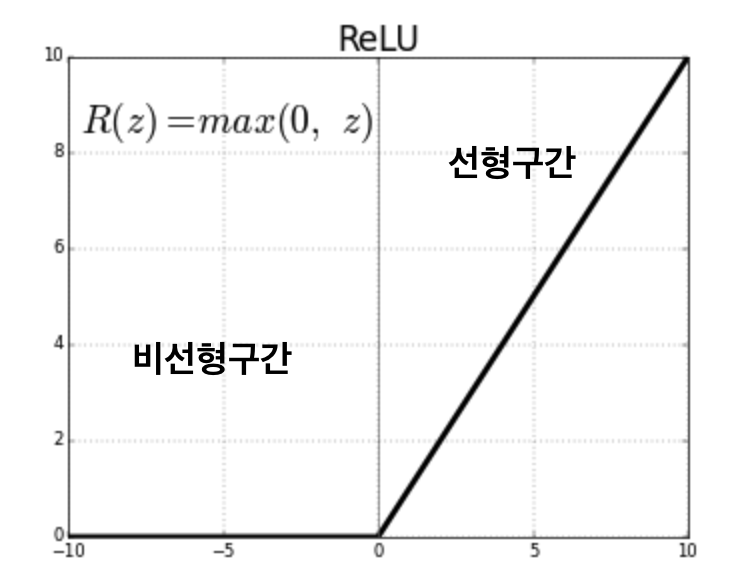
그러나, 이러한 저차원 데이터를 ReLU를 통과하면
0 이하의 값은 0으로, 0보다 크면 선형적으로 작동하므로, 0 이하 값은 정보가 손실 될 수 있어
논문에서는 Linear Bottlenecks에는 비선형적인 ReLU를 사용하지 않고 선형적인 1 X 1 Convolution을 사용하라 얘기합니다.
논문에서는 Manifold에 대한 가설의 실험으로 Linear Bottlenecks 에서 ReLU를 사용하여 더 안 좋은 결과가 나옴을 설명함
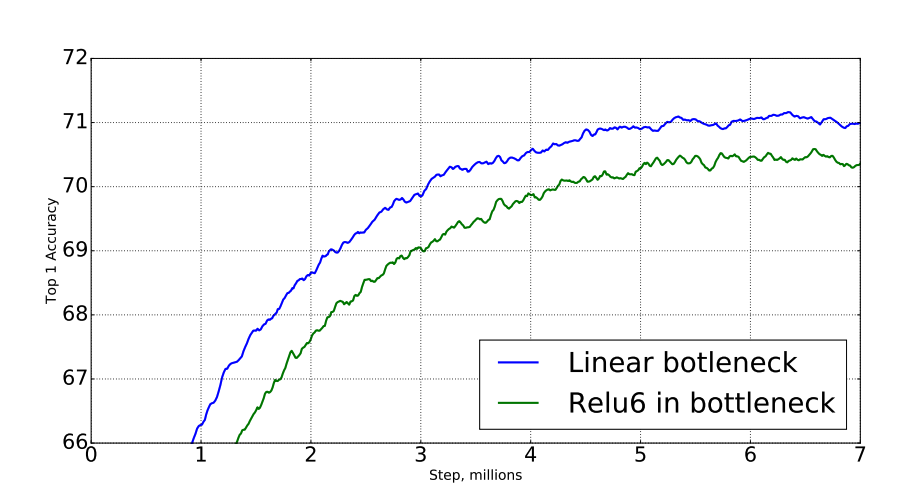
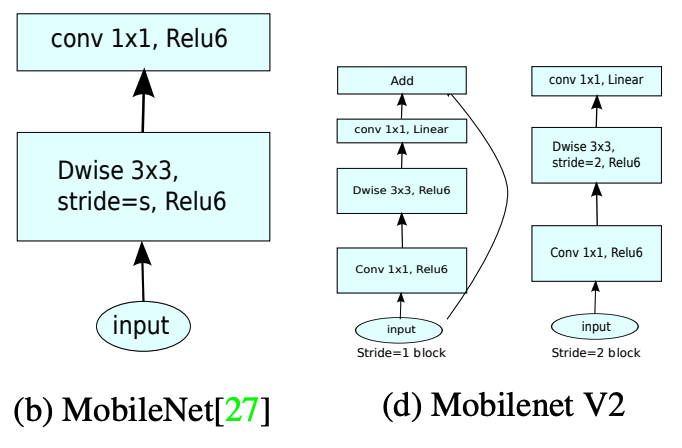
왼쪽 MobileNetV1, 오른쪽 MobileNetV2. Point Wise 부분에서 ReLU6의 여부의 차이점을 볼 수 있다.
4. Inverted Residual
4.1 Residual Block & Inverted Residual Block
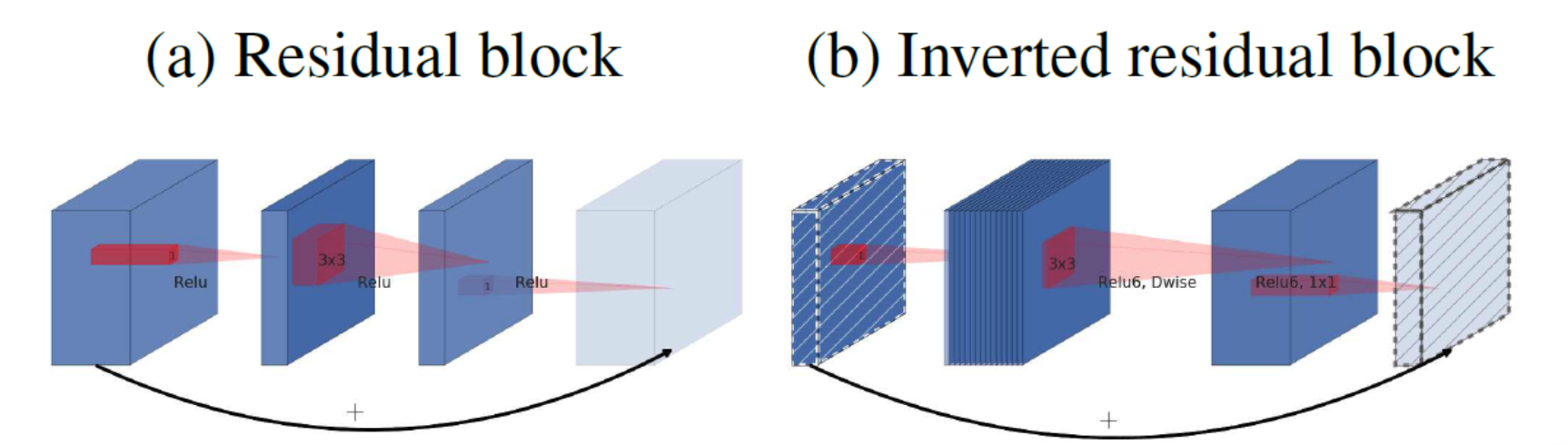
(a) Residual Block
기존 Resnet에서 사용하던 Residual block 과 같습니다.
wide → narrow → wide 형태로 가운데가 좁은 형태로 Bottleneck 구조가 됩니다.
1) Input이 1X1 Convolution을 통해 채널 수를 줄여 Bottleneck 구조를 만듭니다.
2) Bottleneck에서 3X3 Convolution 을 통해 주요 특징을 추출합니다
3) Skip Connection을 위해 다시 1X1 Convolution으로 채널 수를 원래대로 확장합니다.
4) Skip Connection으로 잔차연결하여 신경망이 더 깊어져도 정보 손실이 나지 않게 해줍니다.
(b) Inverted Residual Block
Mobilenet V2에서 제공한 구조로 기존 Residual과 정반대로 narrow → wide → narrow 구조로 되어있습니다. 그래서 Inverted Residual Block.
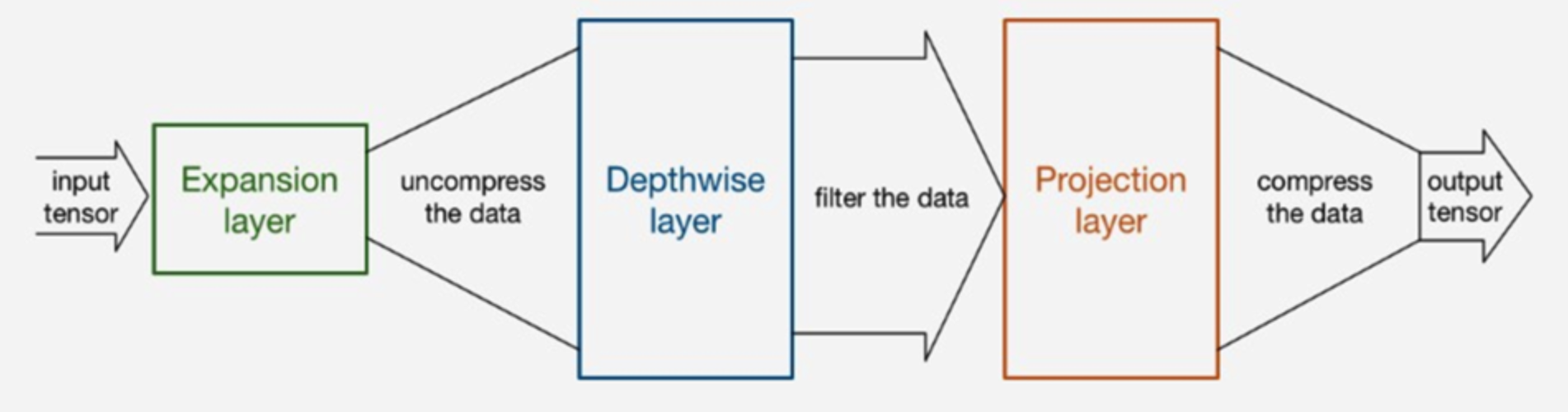
1) Input Tensor가 처음 Inverted Residual Block에 들어온 상태가 narrow 상태
2) Tensor가 Expansion Layer를 통해 채널 수가 확장된 상태가 wide 상태
논문에서는 t (Expansion ratio)로 채널 수를 확장하여 조절한다.
3) Projection layer / Linear Bottlenecks 에서 채널 수가 축소하여 다시 원래 채널 수로 돌아온 상태가 narrow
4) Skip connection으로 원래 입력 값을 출력 값에 더하여 잔차 연결
4.2 Information flow interpretation
논문에서는 MovilenetV2의 아키텍처의 구조가 기존 합성곱에서 얽혀 있던 개념인 Capacity(용량), Expressiveness(표현력)이 분리하여 해석이 가능하다고 해석합니다.
1) Capacity(용량) : 네트워크의 각 레이어가 처리할 수 있는 정보의 양
입력 채널을 축소하는 단계에서 용량에 해당하는 부분. 즉 데이터를 압축하여 핵심 정보를 추출하는 과정(Linear Bottlenecks)
2) Expressiveness(표현력) : 네트워크가 정보를 변환하고 표현할 수 있는 능력
복잡한 패턴을 학습하는 능력으로, Expansion Layer, Depthwise convolution이 표현력 과정이다.
5. Model Architecture
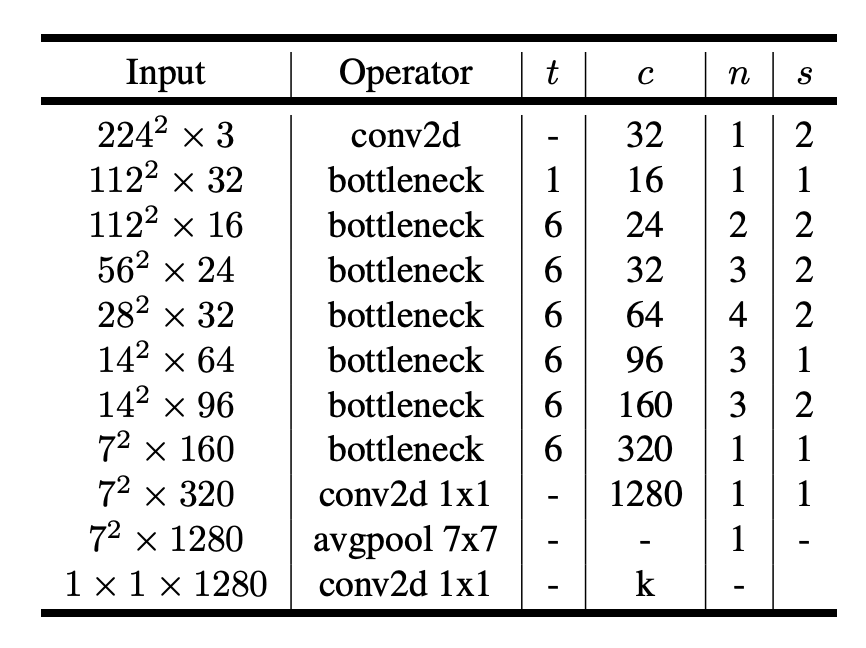
t = expansion ratio
c = output channel
n = number of repeat
s = stride
6. Code
Inverted Residual Block
class InvertedResBlock(nn.Module):
def __init__(self, in_channels, out_channels, t, stride=1): # t = expansion
super().__init__()
self.stride = stride
self.identity = (self.stride == 1 and in_channels == out_channels)
# narrow -> wide
if t != 1:
self.expand = nn.Sequential(
nn.Conv2d(in_channels, in_channels * t, 1, bias=False),
nn.BatchNorm2d(in_channels * t),
nn.ReLU6(inplace=True)
)
# t = 1
else:
self.expand = nn.Identity()
self.depthwise = nn.Sequential(
nn.Conv2d(in_channels * t, in_channels * t, 3, stride=stride, padding=1, groups=in_channels * t, bias=False),
nn.BatchNorm2d(in_channels * t),
nn.ReLU6(inplace=True)
)
# Linear Bottlenecks / wide -> narrow
self.pointwise = nn.Sequential(
nn.Conv2d(in_channels * t, out_channels, 1, bias=False),
nn.BatchNorm2d(out_channels)
)
def forward(self, x):
identity = x
x = self.expand(x)
x = self.depthwise(x)
x = self.pointwise(x)
# Residual
if self.identity:
x = x + identity
return xArchitecture
class MobileNetV2(nn.Module):
def __init__(self, n_classes=1000):
super().__init__()
self.first_conv = nn.Sequential(
nn.Conv2d(3, 32, 3, stride=2, padding=1, bias=False),
nn.BatchNorm2d(32),
nn.ReLU6(inplace=True)
)
self.bottlenecks = nn.Sequential(
self._make_stage(32, 16, t=1, n=1),
self._make_stage(16, 24, t=6, n=2, stride=2),
self._make_stage(24, 32, t=6, n=3, stride=2),
self._make_stage(32, 64, t=6, n=4, stride=2),
self._make_stage(64, 96, t=6, n=3),
self._make_stage(96, 160, t=6, n=3, stride=2),
self._make_stage(160, 320, t=6, n=1)
)
self.last_conv = nn.Sequential(
nn.Conv2d(320, 1280, 1, bias=False),
nn.BatchNorm2d(1280),
nn.ReLU6(inplace=True)
)
self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
self.fc = nn.Sequential(
nn.Dropout(0.2),
nn.Linear(1280, n_classes)
)
def forward(self, x):
x = self.first_conv(x)
x = self.bottlenecks(x)
x = self.last_conv(x)
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.fc(x)
return x
def _make_stage(self, in_channels, out_channels, t, n, stride = 1):
layers = [InvertedResBlock(in_channels, out_channels, t, stride)]
in_channels = out_channels
for _ in range(n-1):
layers.append(InvertedResBlock(in_channels, out_channels, t))
return nn.Sequential(*layers)7. Experiments
Classification
Data : Flower102
Epoch : 120 (Early Stopping : 27)
Optimizer : RMSprop, momentum=0.9, weight decay =0.00004
Batch Normalization
Initial Learning Rate=0.045 Learning Rate Decay=0.98 per epoch
batch size : 96
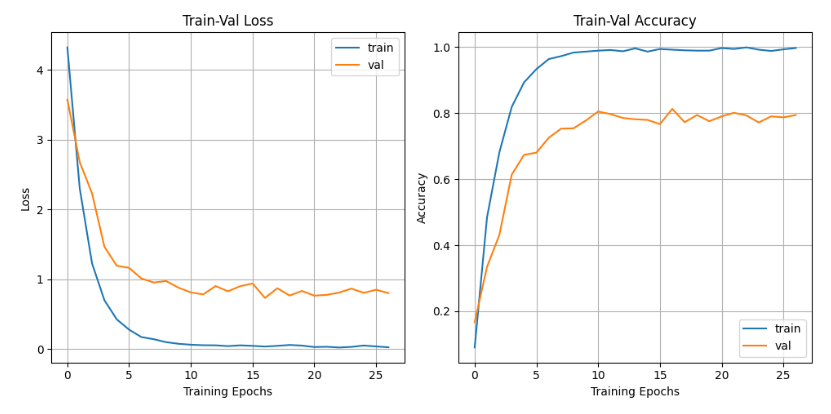
Minimum Train Error Rate: 0.10%
Minimum Val Error Rate: 18.73%
Maximum Train Accuracy: 1.00%
Maximum Val Accuracy: 0.81%
