• prediction
  인풋 : MDP와 Policy output : value function !

• control
  인풋 : MDP output : optimal value function과 optimal policy

=> 결국, 핵심은 맨 위에 있는 하얀색 값을 얻기 위해서는 4개의 하얀색 값을 활용하면 된다! 이얘기!
=> 맨 위의 하얀색 = sigma (흰->검 이 될 확률 x (검은색에서의 보상 + sigma(검->흰이 될 확률 x 흰에서의 보상))
=> 맨 위의 하얀색 =

여기서의 핵심은 이 검은색! 이 정확하다는 것!
=> 이 정확한 검은색을 통해서 계속 계속 들어갈 수 있다!

여기서의 policy는 random policy.
동서남북으로 갈 수 있음!

• k = 0
  흰에서의 보상은 0
• k = 1
  흰에서의 보상은 -1

1. 좌상단 & 우하단 제외
   $v_{1}(s)$ = $ 1/4 \times (-1 + 0) + 1/4 \times (-1 + 0 ) + 1/4 \times (-1 + 0 ) + 1/4 \times (-1 + 0) = -1$

   맨 위의 하얀색 = sigma (흰->검 이 될 확률 x (검은색에서의 보상 + sigma(검->흰이 될 확률 x 흰에서의 보상))
   => -1 = sigma ( 1/4 x (-1 + 0 ))

2. 좌상단 & 우하단
   $v_{1}(s)$ = $ 1/4 \times (-1 + 0) + 1/4 \times (-1 + 0 ) + 1/4 \times (-1 + 0 ) + 1/4 \times (-1 + 0) = -1$

   policy는 계속해서 1/4인데 동일한데 그럼 계산이 어떻게 되는 거지?

• k = 2

1. -1.7

$v_{2}(s)$ = $ 1/4 \times (-1 + 1 \times -1) + 1/4 \times (-1 + 1 \times -1) + 1/4 \times (-1 + 1 \times -1 ) + 1/4 \times (-1 + 0) $

2. -2.0

$v_{2}(s)$ = $ 1/4 \times (-1 + 1 \times -1) + 1/4 \times (-1 + 1 \times -1) + 1/4 \times (-1 + 1 \times -1 ) + 1/4 \times (-1 + 1 \times -1) $

-> greedy하게 움지이기만 해도 best policy를 찾을 수 있다.
-> 그니까, k=2를 예시로 들자면, v(s)= -1.7인 경우엔 0으로 가는 게 가장 greedy한 선택이고, -2.0인 경우에는 -1.7으로 가는 게 greedy한 거겠지?

무한하게 가지 않더라도. 어쨌뜬 optimal policy를 도달했다.

여기에서의 optimal policy란?
일단 policy의 정의 자체가
$Phi(a|s)$ = $P[A_t = a| S_t = s]$
이기 때문에 ,
무조건 내가 어떤 state에 있던 간에 나는 best policy를 안다! 이것보다는,
특정 state에 있을 때 내가 어떻게 선택해야지 가장 좋을지를 안다! 이런 느낌~

Policy Iteration

Policy Iteration은
evaluate(평가) : value function 을 찾고 improve (그 value function에 대해 greedy하게 움직이는 policy를 찾는)

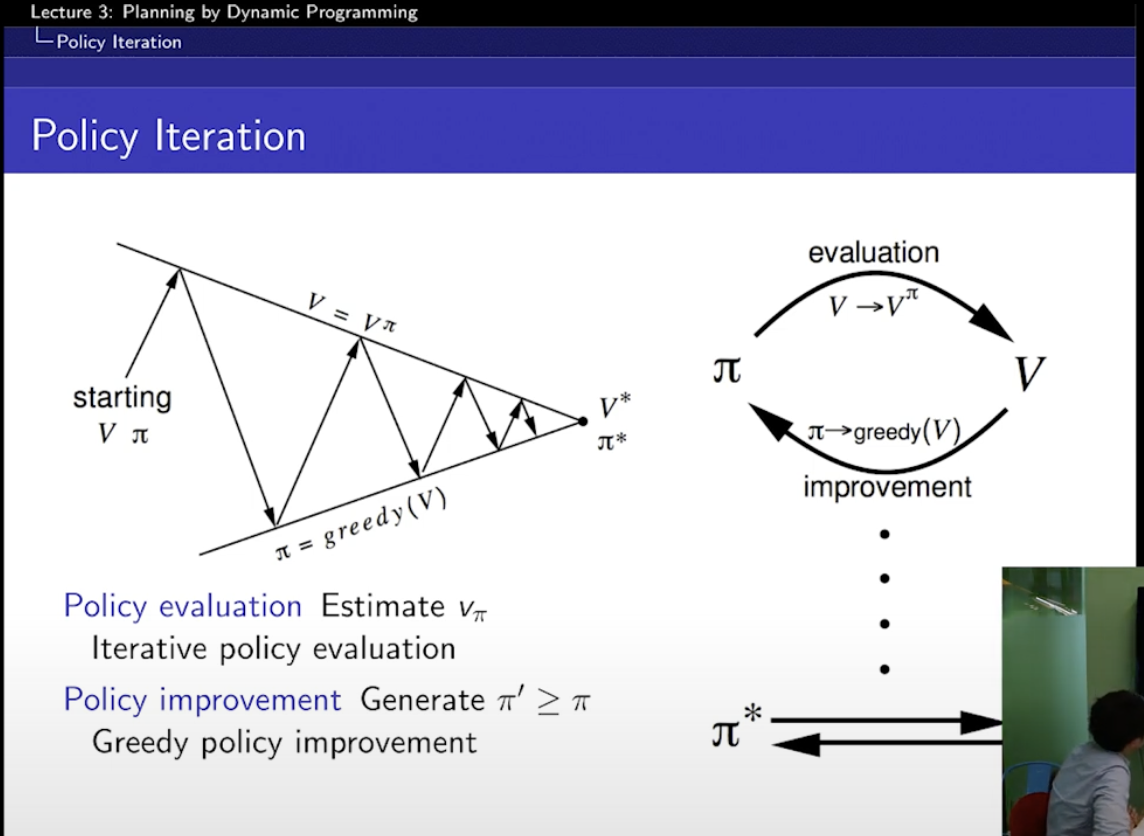
계속해서 결국 star에 도달하기 위한 여정!

improve하면 이전 Policy보다 더 좋다!

일찍 끝내면 안되니?

Value Iteration

value iteration은

: 팡요랩에서도 이해를 못했다고 한다?
: 그냥 policy가 과연 s에서 optimal state를 얻을 수 있을까? 그렇다면 어떤 조건이 무조건 필요한 걸까?
-> s'이 s로부터 도달 가능할 때,
-> policy를 통해 s'으로부터 optimal value를 얻을 수 있다.