[강화학습 스터디] 7강 Policy Gradient + 구현 코드

#### 1.  Monte Carlo Control Policy #### 
#==============================================================================

import numpy as np

num_states = 5
num_actions = 2
num_episodes = 5000

theta = np.random.randn(num_states, num_actions)  # 각 상태에서 행동별 가중치
#원래 사실 theta를 어떻게 initialize 해야하는지 감이 안잡혔었음.

# Softmax 정책 함수
def softmax_policy(state, theta):
    preferences = theta[state]  # 해당 상태의 행동별 가중치 가져오기
    exp_values = np.exp(preferences - np.max(preferences))  # 안정적인 softmax
    return exp_values / np.sum(exp_values)

# 확률에 따라 행동 선택
def choose_action(state, theta):
    probs = softmax_policy(state, theta)
    return np.random.choice(num_actions, p=probs)


# 한 번의 에피소드를 실행하면서 데이터를 모으는 코드 (Monte Carlo)
def run_episode(theta, max_steps=10):
    episode = []
    state = np.random.randint(0, num_states)  # 랜덤한 초기 상태

    for _ in range(max_steps):  # max_steps 이후 종료
        action = choose_action(state, theta)
        next_state = np.random.randint(0, num_states)
        reward = np.random.randn()
        
        episode.append((state, action, reward))
        state = next_state

    return episode

alpha = 0.01  # 학습률
gamma = 0.9   # 감가율 (할인율)

# GLIE Monte Carlo Control 학습
for episode_num in range(1, num_episodes + 1):
    episode = run_episode(theta) 
    
    G = 0  # 리턴값 초기화

    for state, action, reward in reversed(episode):
        G = reward + gamma * G  # 할인된 보상 계산
        probs = softmax_policy(state, theta)

        grad = np.zeros_like(theta[state])
        #gradient를 저장하는 저장소! 
        grad[action] = 1 - probs[action]  # log 확률의 gradient가 이렇게 계산이 되고 
        #여기서 헷갈렸던 건, 선택한 행동 선택한 행동 a에 대해서만 기울기를 계산
        theta[state] += alpha * grad * G  # 정책 파라미터 업데이트
        #alpha * log gradient * G 이렇게 되는 것임. 

# 학습된 파라미터 출력
print("Theta:")
print(theta)



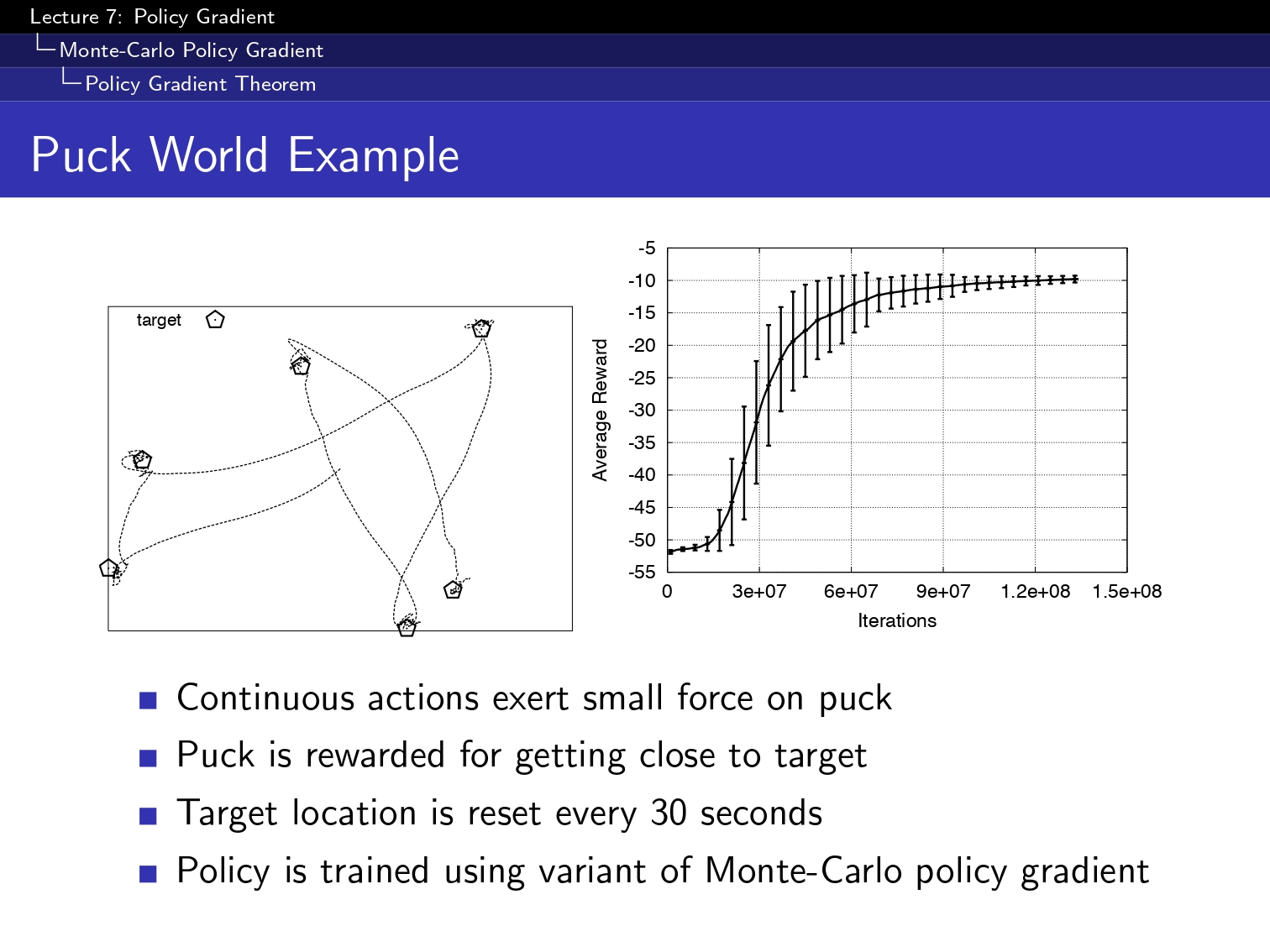
#### 2.  Action Value Actor Critic #### 
#==============================================================================

import numpy as np

num_states = 5
num_actions = 2
num_episodes = 5000

theta = np.random.randn(num_states, num_actions)  # 각 상태에서 행동별 가중치
#원래 사실 theta를 어떻게 initialize 해야하는지 감이 안잡혔었음.
w = np.zeros(num_states * num_actions)  # VFA에서 사용할 가중치 초기화

# Softmax 정책 함수
def softmax_policy(state, theta):
    preferences = theta[state]  # 해당 상태의 행동별 가중치 가져오기
    exp_values = np.exp(preferences - np.max(preferences))  # 안정적인 softmax
    return exp_values / np.sum(exp_values)

# 확률에 따라 행동 선택
def choose_action(state, theta):
    probs = softmax_policy(state, theta)
    return np.random.choice(num_actions, p=probs)
    #행동 선택 

# 한 번의 에피소드를 실행하면서 데이터를 모으는 코드 (Monte Carlo) : 이건 필요 x .왜냐면 매스텝마다 update하니까. 
#def run_episode(theta, max_steps=10):


alpha = 0.01  # 학습률
gamma = 0.9   # 감가율 (할인율)



def feature_vector(state,action,num_states,num_actions):
    vec = np.zeros(num_states * num_actions)
    vec[state * num_actions + action] = 1  
    return vec

def VFA(state, action, w):
    return np.dot(w, feature_vector(state, action, num_states, num_actions))  # 가중치와 특징 벡터의 내적

  
  
for episode_num in range(1, num_episodes + 1):
    state = np.random.randint(0, num_states)  # 초기 상태
    action = choose_action(state, theta) #action 고르고 

    #여기서 state,action,reard in reversed(episode)할 필요가 없는 게, 이건 매번 update다.
    for _ in range(10):  # 최대 10 스텝
        reward = np.random.randn()  # 보상 샘플링
        next_state = np.random.randint(0, num_states)  # 환경에서 다음 상태 샘플링
        next_action = choose_action(next_state, theta)  # 정책에 따라 다음 행동 선택
        
        delta = reward + gamma * VFA(next_state, next_action, w) - VFA(state, action, w)  # TD error


        # 크리틱 업데이트 (w 업데이트)
        w += alpha * delta * feature_vector(state, action, num_states, num_actions)

        # 액터 업데이트 (theta 업데이트)
        probs = softmax_policy(state, theta)
        grad = np.zeros_like(theta[state])
        grad[action] = 1 - probs[action]
        theta[state] += alpha * grad * delta

        # 다음 스텝으로 이동
        state, action = next_state, next_action        

# 학습된 파라미터 출력
print("Theta:")
print(theta)

6강에 있는 내용들 그대로 이해하기 쉽게 조금만 바꿔서 해보았습니다!!!!!

5강에서 한번 개념 제대로 잡으니까, 그냥 지식 업데이트만 하면 되는 느낌이더라구용!!!
혹시 질문이 있다면,,,댓글을 남겨주세요!!