MDP는 일종의 environment를 표현하는 방법!
대부분의 모든 RL problem은 MDP로 표현할 수 있다고 한다.

Markov Process -> MarKov Reward Process -> Markov Decision Process
이렇게 확장이 된다.

일단 MarKoV 특성

예전의 것들은 현재랑 관계가 없다.
state만 필요할 뿐, 이전 history는 필요가 없다.

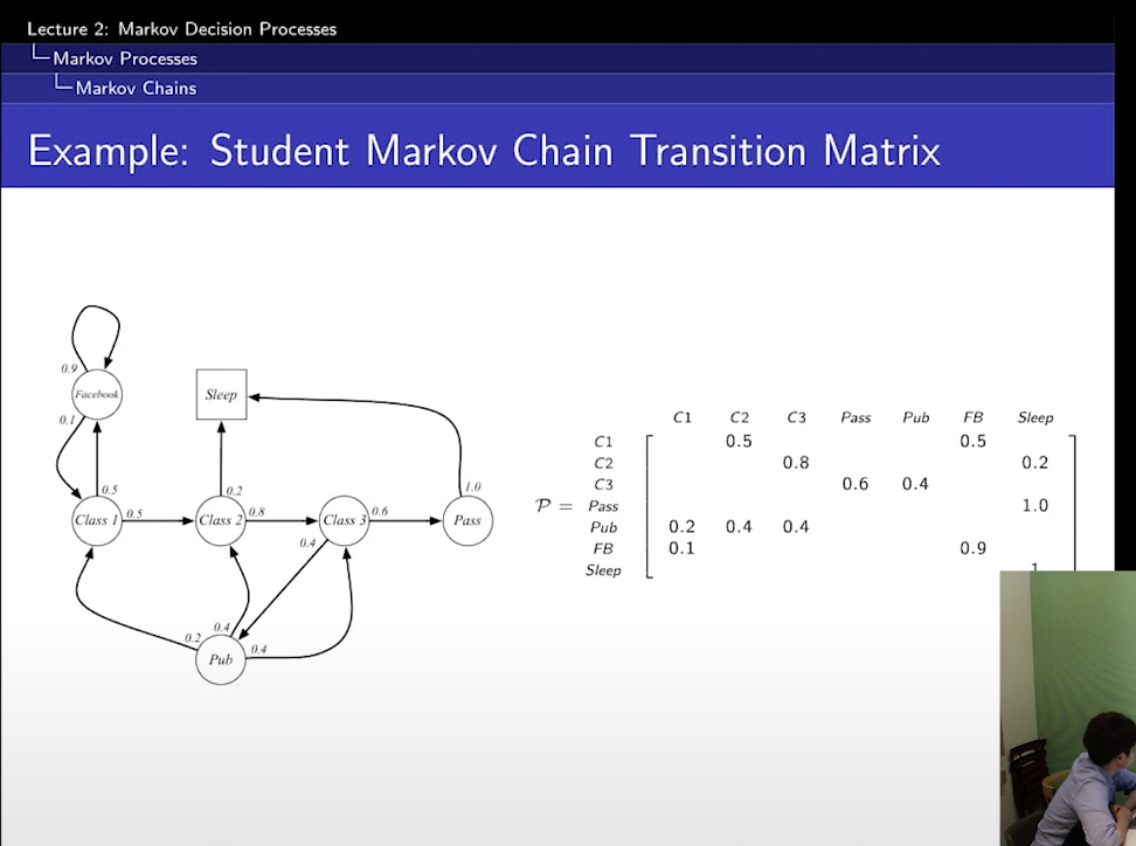
• State Transition Matrix
  

s에서 s'으로 갈 확률을 Pss'라고 하는데,

그것들을 이제 저렇게 matrix로 모아 놓은 게 P라고 생각하면 됨.
n x n

1. markov process

: 상태들이 n개가 있고 discrete하게 state를 옮겨다니는!
state는 stochastially 움직이는 !

S = state들의 집합
P = 전이 확률 matrix

random process : 샘플링을 할 수 있다.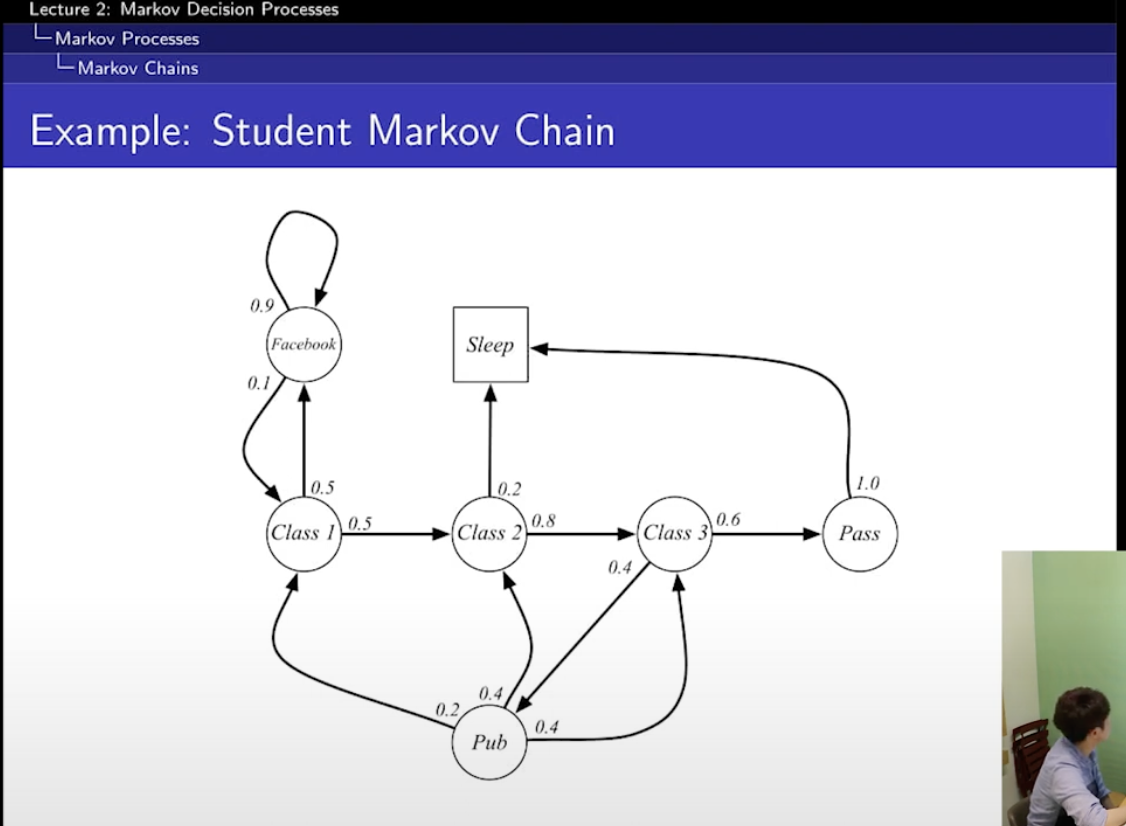

여기서 state는 7개!
state의 전이 확률이 화살표...! 오오

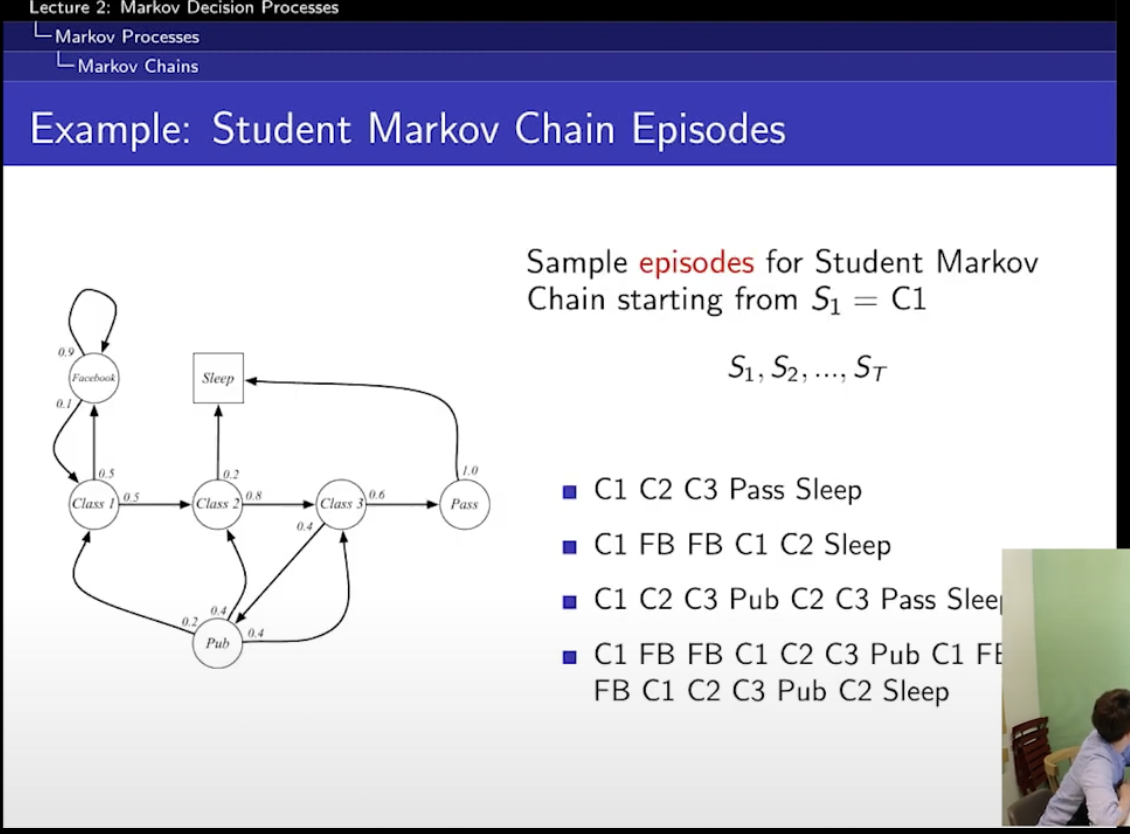
여기서, sampling을 해볼 수가 있음.

episode란?
처음부터 시작해서 final까지 가는 것!

시작이 C1이라 하면, 그 뒤에 C2,C3

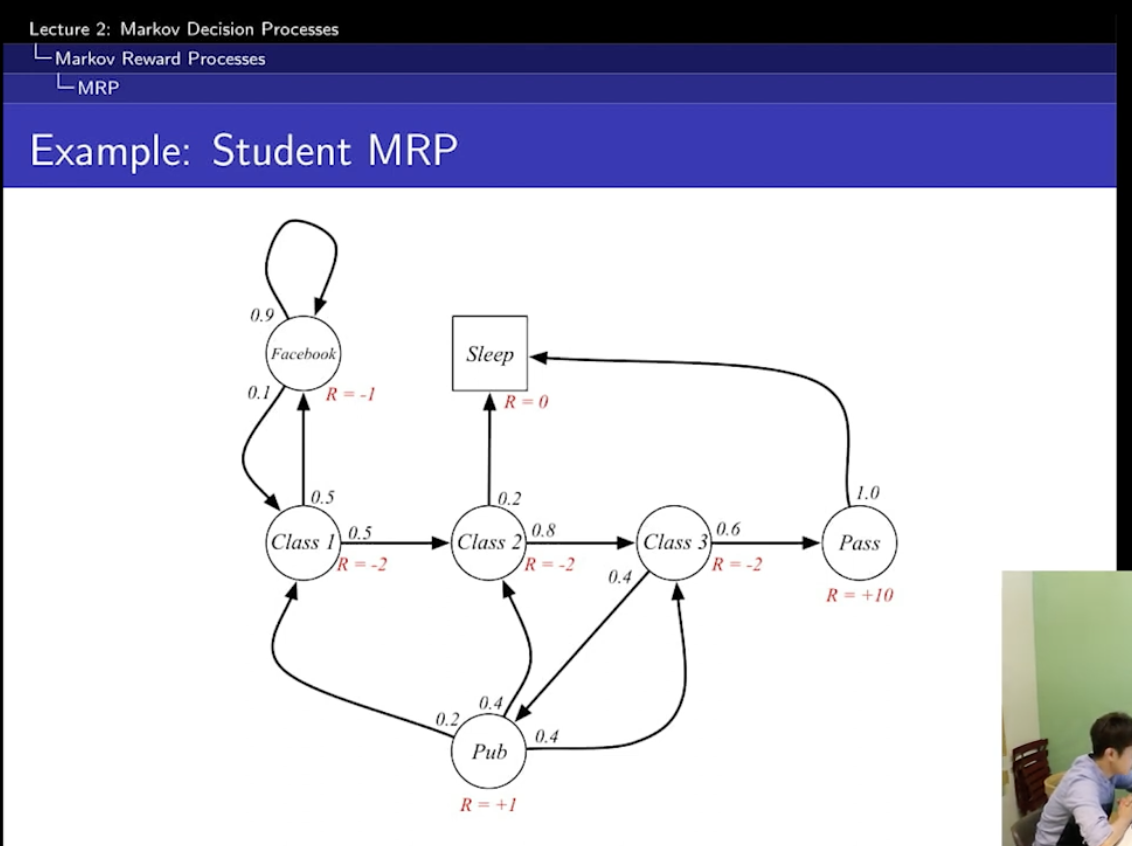
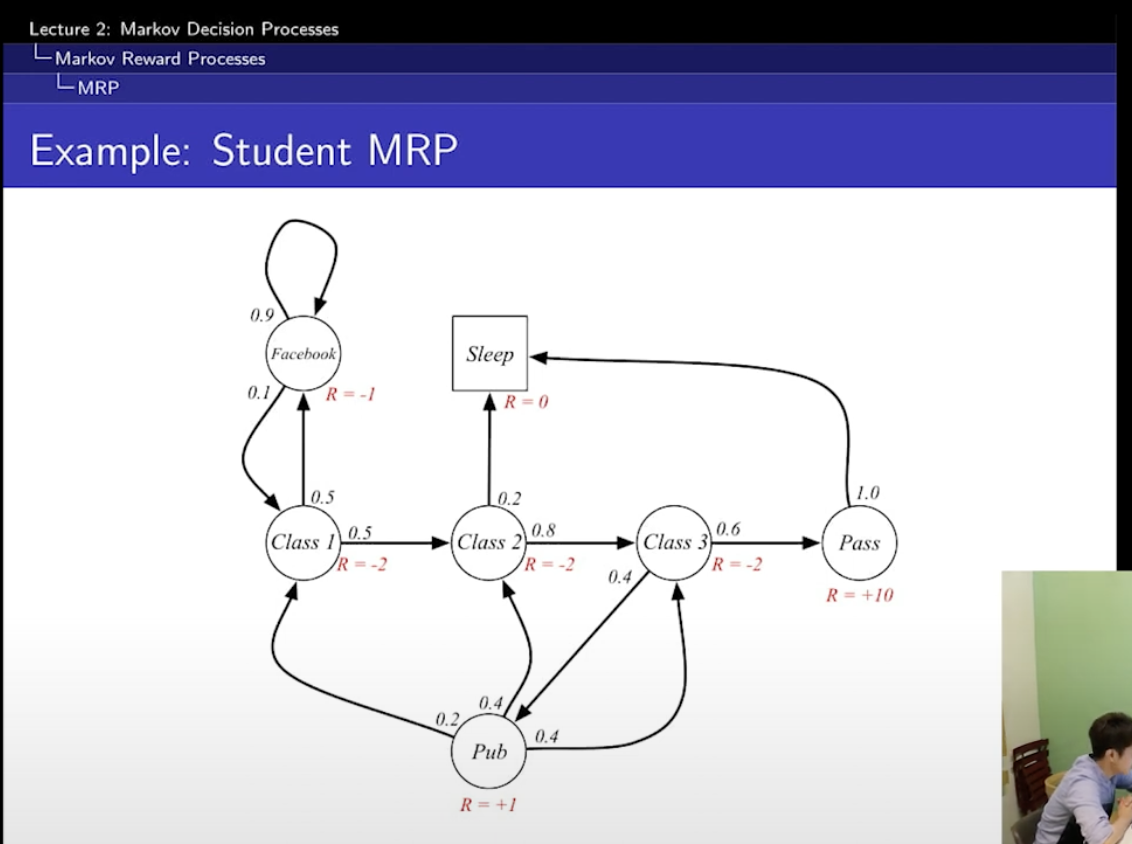
2. markov reward process

= markov chain + rewards 하지만 action은 없다.

아까는 S,P였는데 R,r이 필요
R은 reward function
r은 discount factor

R에 있는 수는?
그냥 뭐 예시다.

이거는 action이 없기 때문에 확률적으로 그냥 그 확률을 따라가서 reward를 주는 거다.
그래서 action이 결부될 일이 없음.

강화학습은 이 return을 maximize하는 것이 핵심이다.
경로동안 받는 보상들의 총합!!!
감마가 1 : 멀리 보는 거 = 미래의 보상도 현재 보상만큼 중요시 !
감마가 0 : 단기

Horizon = 얼마나 많은 state만큼 진행이 되는건지!

discount 왜 해?

1. 수학적으로 편리해서

state value function은, reward의 총 기댓값