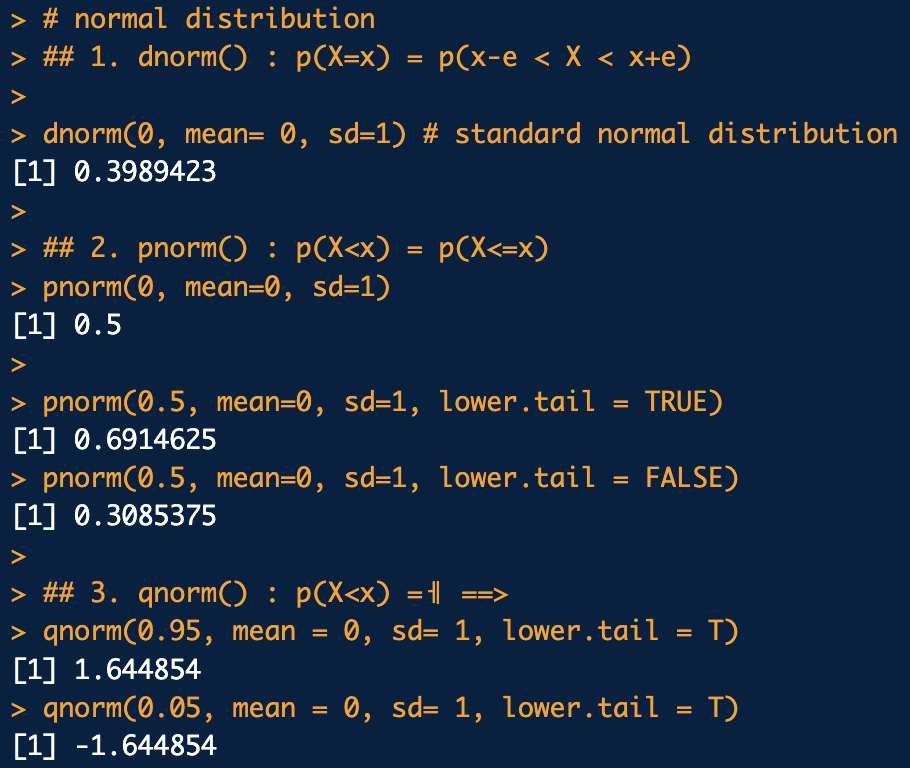
dnorm() -> 수치형 확률변수 X가 x의 확률을 계산
pnorm() -> 확률변수 X가 x보다 작을 확률
lower.tail 0보다 클 확률을 계산 또는 0보다 작을 확률을 계산
인자를 'FALSE'로 설정하면, 확률밀도함수의 우측 면적을 계산
qnorm() -> X가 x보다 작을 확률이 p일 때 x를 계산
rnorm() -> 정규분포에서 난수를 뽑을 수 있음
sample = rnorm(1000, mean = 0, sd=1)
hist(sample)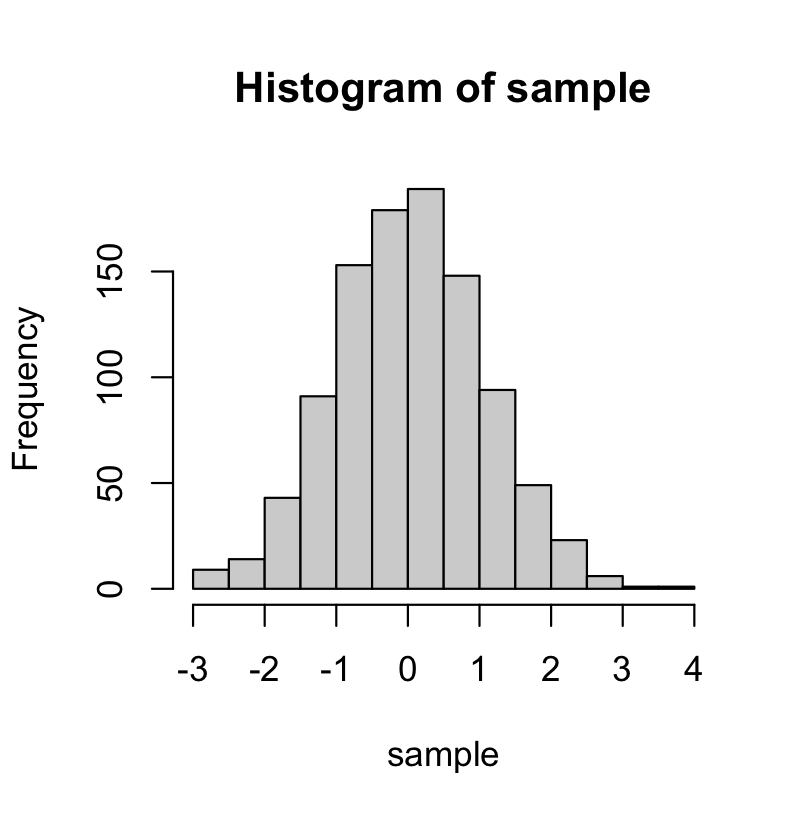
표준정규분포
통계량의 분포를 표본분포라고 한다. 통계량은 표본평균일수도 있고 표본분산일수도 있다.
모집의 분포가 표준정규분포인 경우 Z ~ N(0,1)로 표기
카이제곱분포
카이제곱분포의 확률밀도함수의 모수는 자유도 k 하나로서, k 값에 따라 밀도함수의 형태가 k가 커지면 점점 정규분포에 근사하게 됨
dchisq(), pchisq(),rchisq()
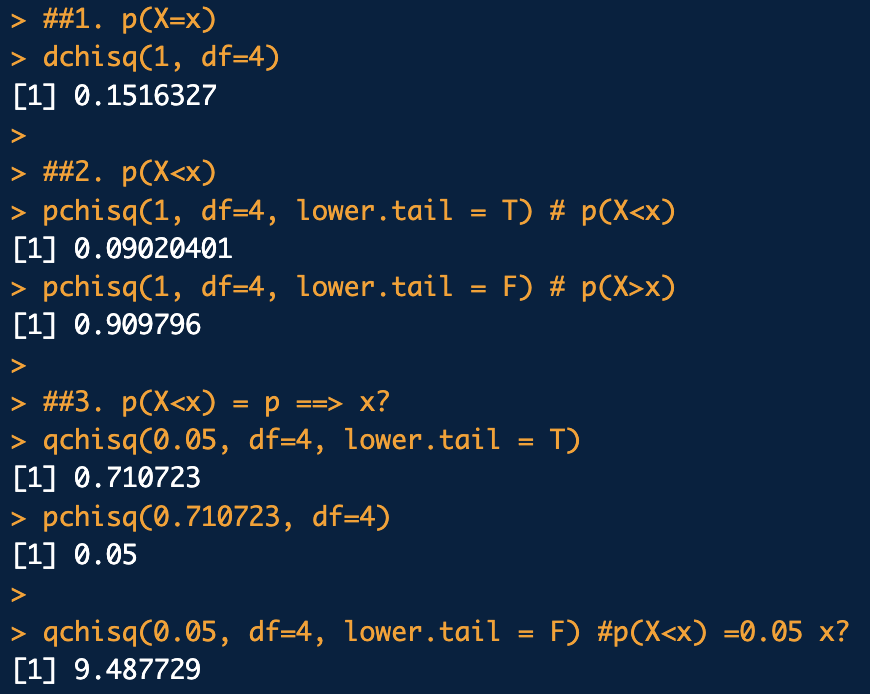
sample = rchisq(1000, df =4)
hist(sample)
t분포
표준정규분포 N(0,1)을 따르는 확률변수 Z
t분포의 기호 : T ~t(u)
t분포의 모수 : 자유도
dt() 함수를 통해 분포 확률밀도함수에서 특정 x값에 대응하는 y값을 출력
pt() 함수를 통해 특정 x값을 기준으로 확률밀도함수의 좌측 면적을 계산 qt() 함수의 lower.tail을 'FALSE'로 설정하면 확률밀도함수의 우측 면적을 기준으로 x값을 계산
rt()함수를 통해 t분포에서 난수를 뽑을 수 있음
F분포
df()함수의 인자 df1=, df2= 를 통해 F분포의 자유도를 설정할 수 있음
pf()함수를 통해 특정 x값을 기준으로 확률밀도함수의 좌측 면적을 계산 할 수 있음
qf()함수로 특정 면적에 해당하는 x값을 계산할 수 있음
rf() 함수를 통해 정규분포에서 난수를 뽑을 수 있음
sample()함수의 인자 x=는 모집단, 인자 size= 샘플 개수를 설정
set.seed()함수로 random seed를 주어서 항상 동일한 표본이 뽑히도록 고정
- 출처 통계청 통계교육원