Intro
이번 블로그에서는 복잡한 neural network system에서 gradient를 게산하는 방식인 backpropagation에 대해서 알아보려고 합니다.
머신러닝, 딥러닝을 접하게 된다면 gradient 와 backpropagation에 대해 많이 들을 것입니다. 어려운 개념이지만 아래의 내용들을 통해 이해가 되길 바랍니다.
Compute gradients
*Gradients를 구하는 방식
- Nonlinear score function
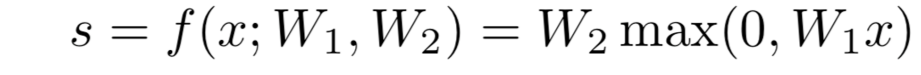
- SVM Loss on predictions
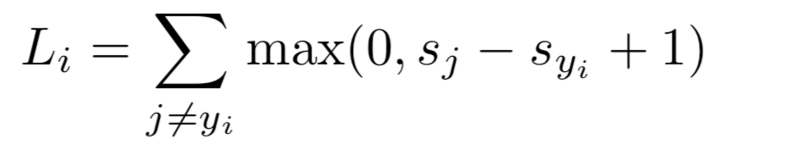
- Regularization
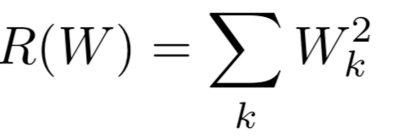
- Total loss = data loss + regularization
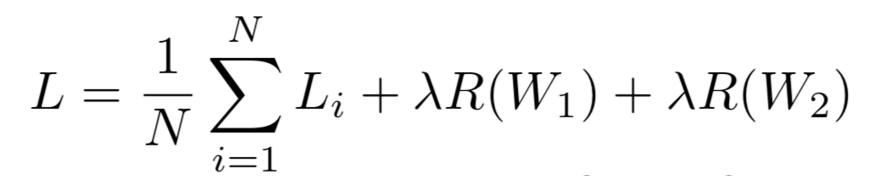
- Derive on paper (bad idea)
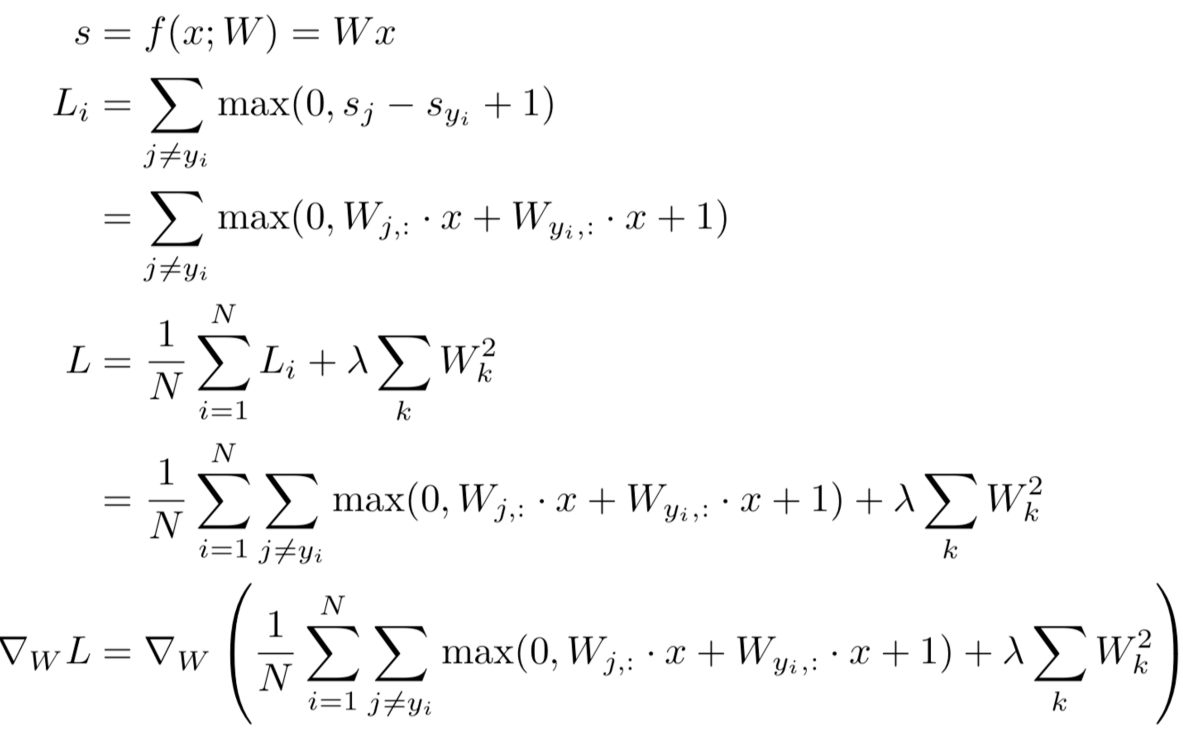
-
Very tedious
- lost of matrix calculus
- need lots of paper
-
Change loss
-
use scratch
-
Not modular
-
-
Not feasible on complex models
- Computational Graph(better idea)
모델에서 이뤄지는 계산들을 그래프의 형태로 나타낸 것입니다.
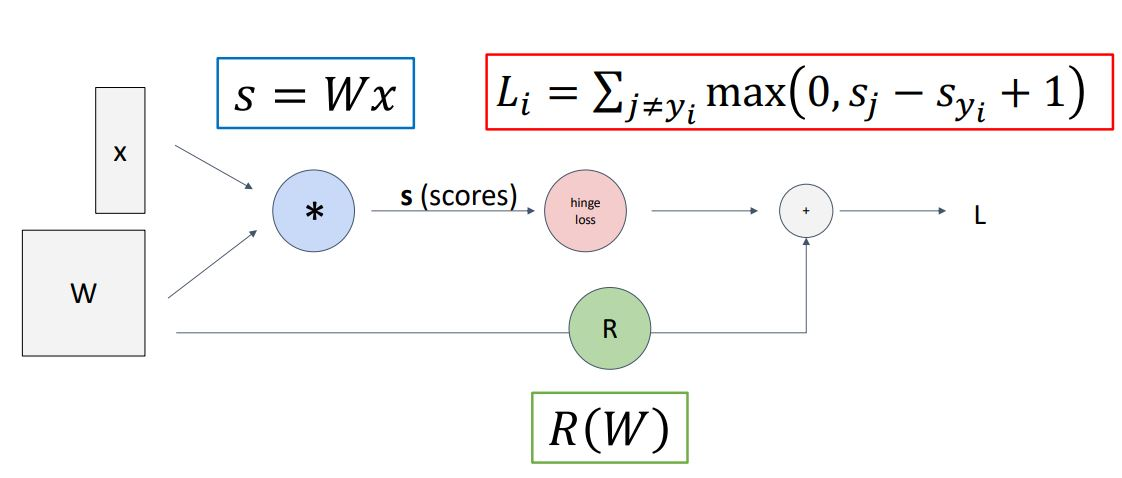
위의 그림은 linear classifier model의 loss를 계산하는 과정이고 파트별로 나눠서 graph로 나타낸 것입니다.
*파트별: hypothesis function, loss function, regularization term
강의에서도 말했지만, 단순한 구조에서는 엄청나게 이득이 보이지 않을지라도 모델이 커지고 복잡해지면 이 방식을 유용하게 사용할 겁니다.
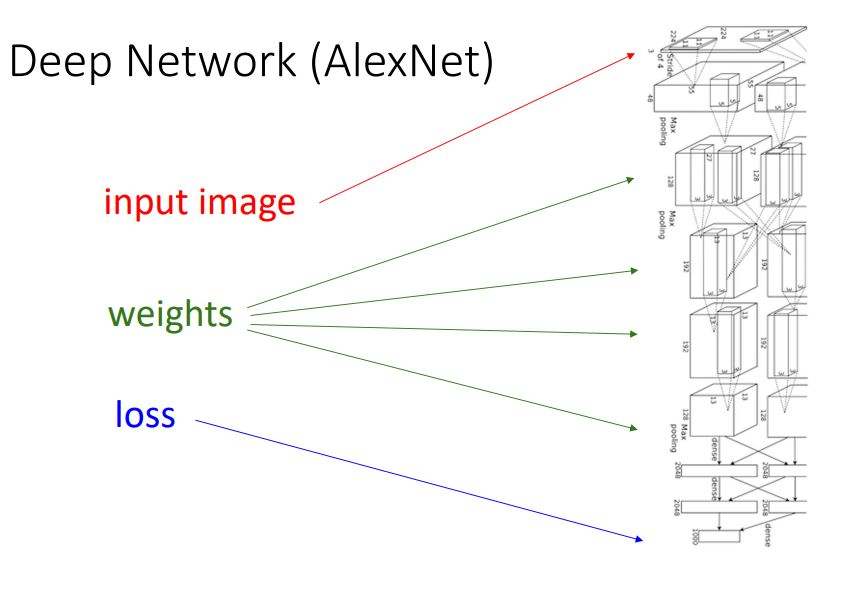
6. AlexNet
Deep network로 많은 layer쌓기와 computational graph를 이용한 계산과정을 통해 모델을 구조화 한 것입니다.
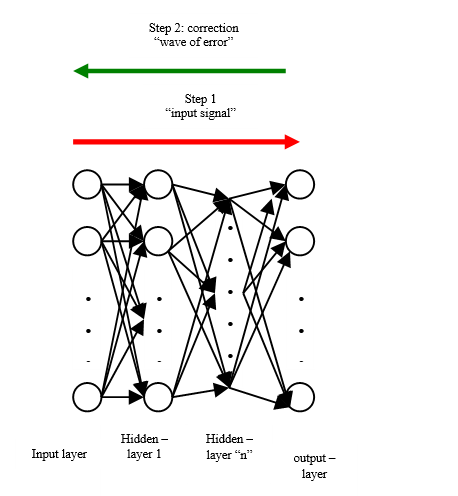
Backpropagation
출력층에서 입력층 방향으로 계산하면서 가중치를 업데이트하는 알고리즘입니다.
그러면 이제 예시를 통해 과정을 설명합니다.
- 함수를 computational graph로 표현하고 backpropagation을 사용해 gradient계산
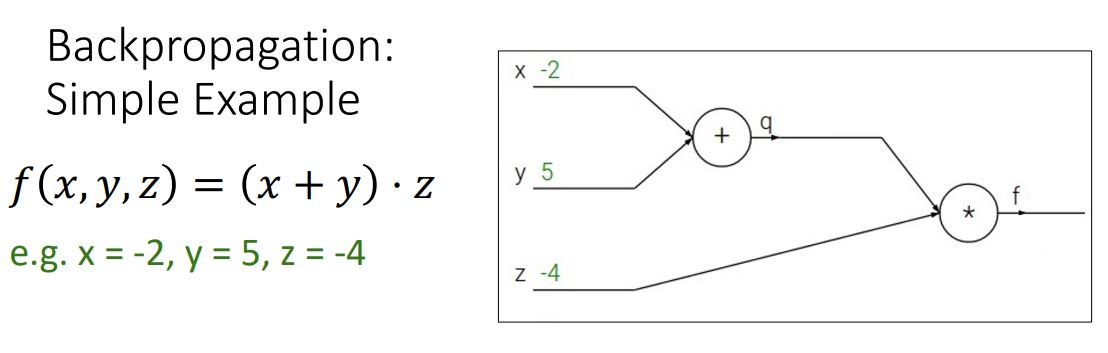
1-1) 순방향: compute output
computational graph로 input 값을 계산하여 output 값을 나오게 합니다.
- 초록색 숫자
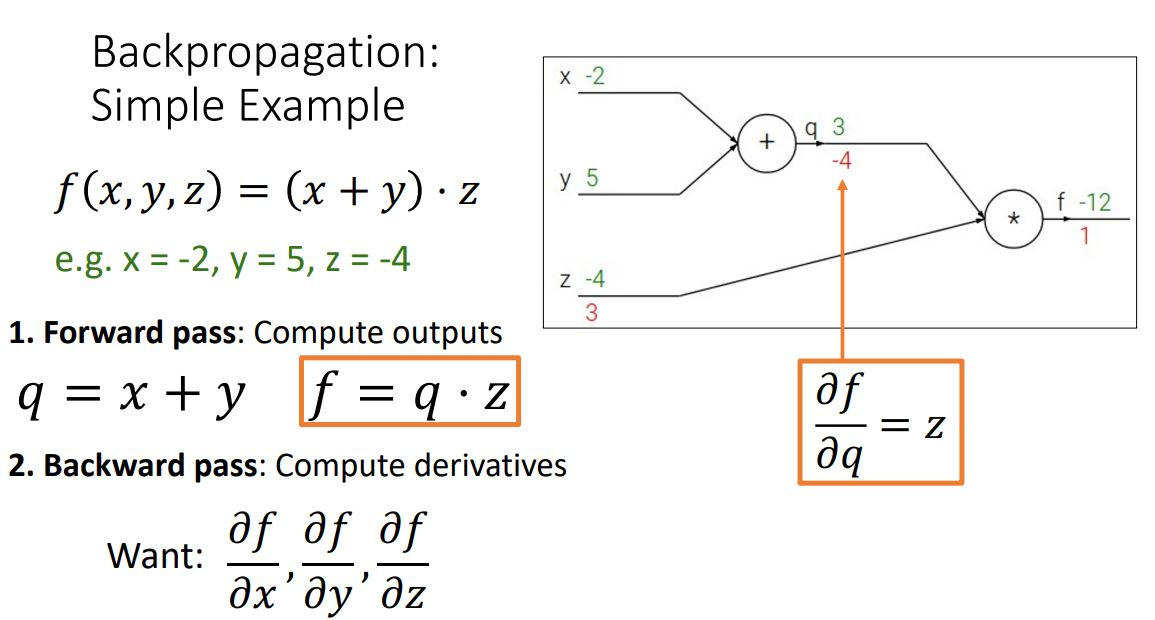
1-2) 역전 방향: Compute derivatives
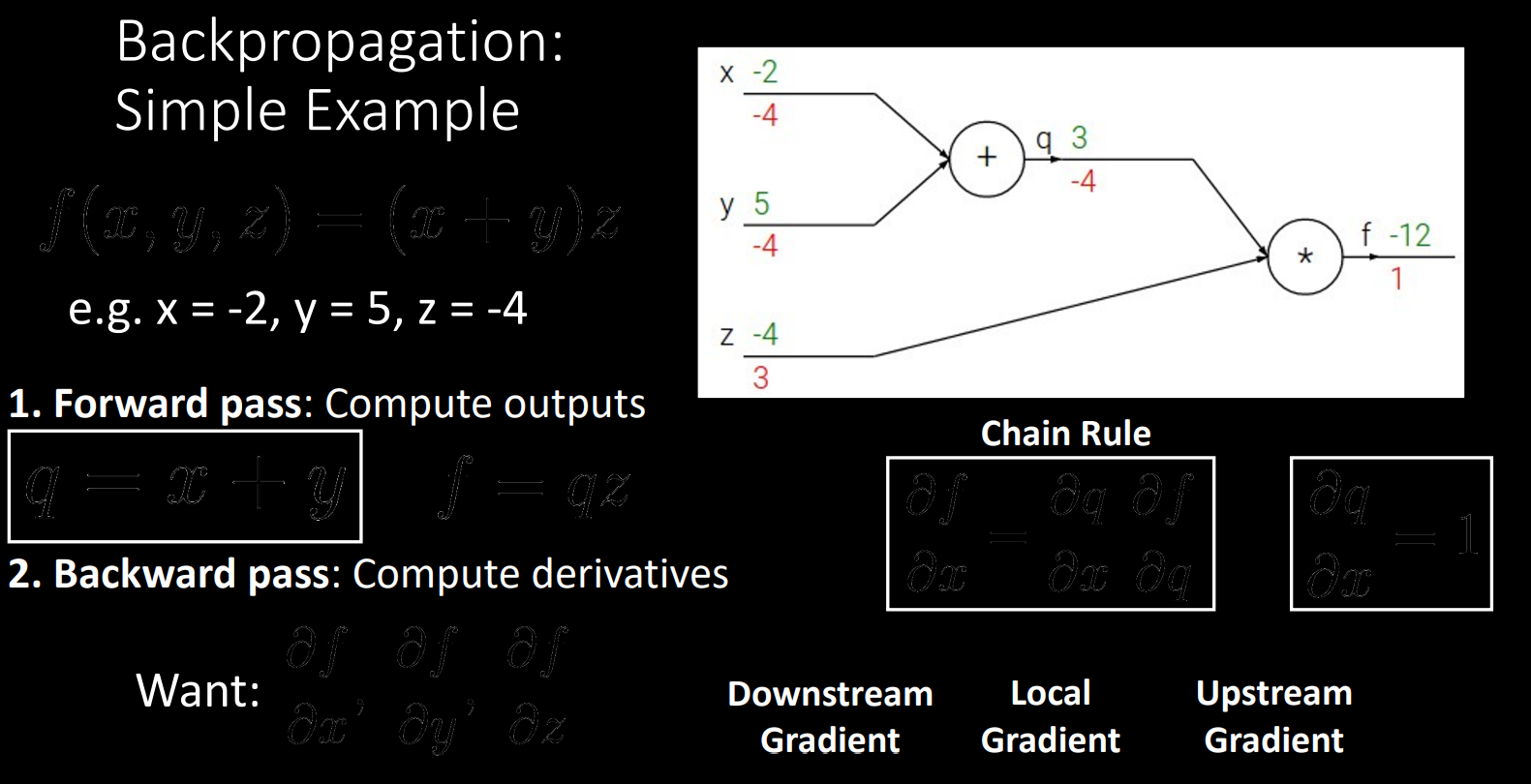
-
output부터 inpute까지의 모든 노드를 편미분하여 upstream gradient 만들기
-
Chain rule이용하여 local gradien만들기
-
Upstream gradient 곱하기
-
상위의 노드 gradient 계산하기
-
즉, input의 gradient를 게산하는 과정
1-3) 그림으로 정리
- logistic classifier의 함수를 computational graph로 나타낸 후 backpropagation 사용하여 gradient 계산
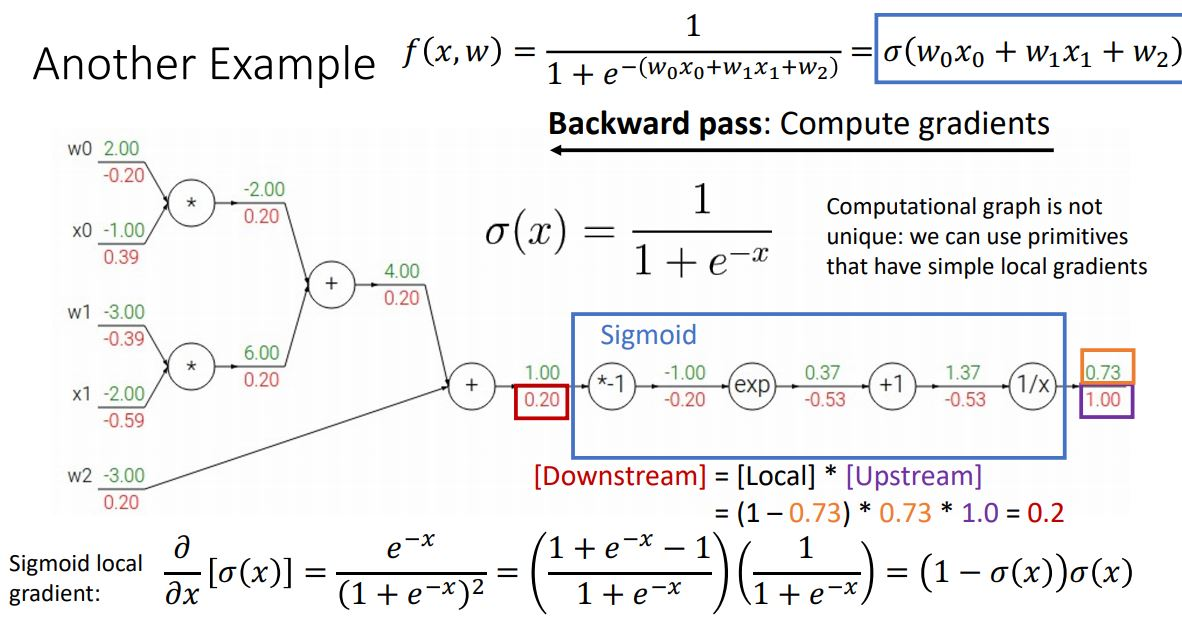
-
logistic classifier함수를 computational graph로 나타냄
-
forward pass를 통해 output게산
-
backward pass 이용
- downstream gradient계산: 최종 input의 gradient 게산 가능
- primitive function 사용(sigmoid,...등)
*sigmoid는 미분의 형태가 간단하여 효율적으로 gradient를 계산
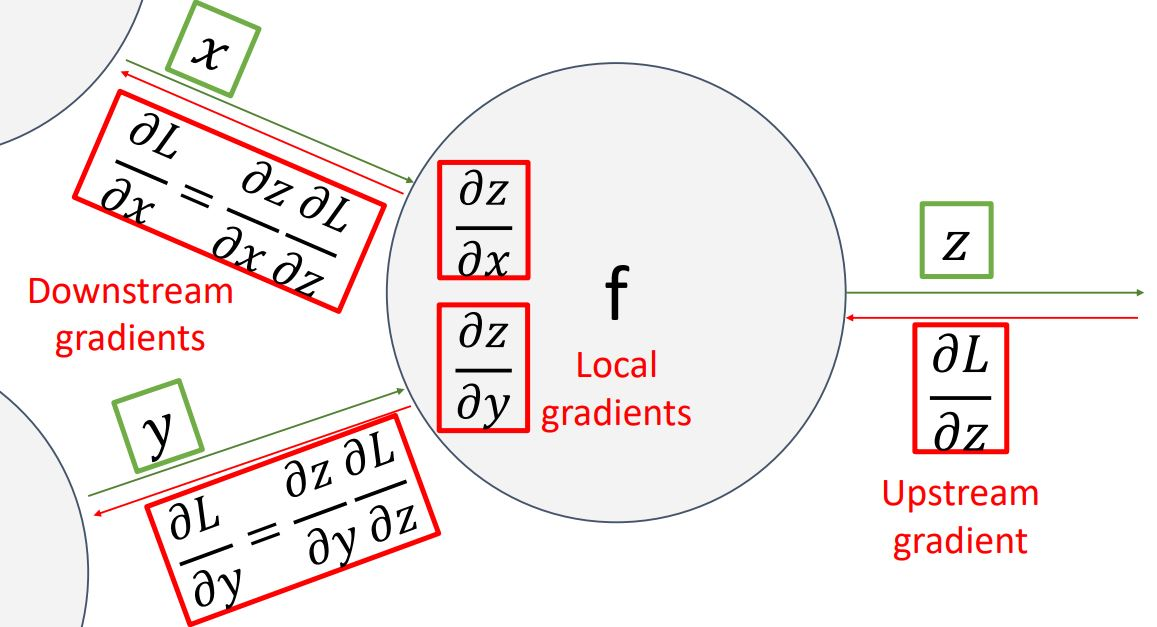
3. gradient flow in backpropagation
computational graph는 특정 gate의 역할입니다.
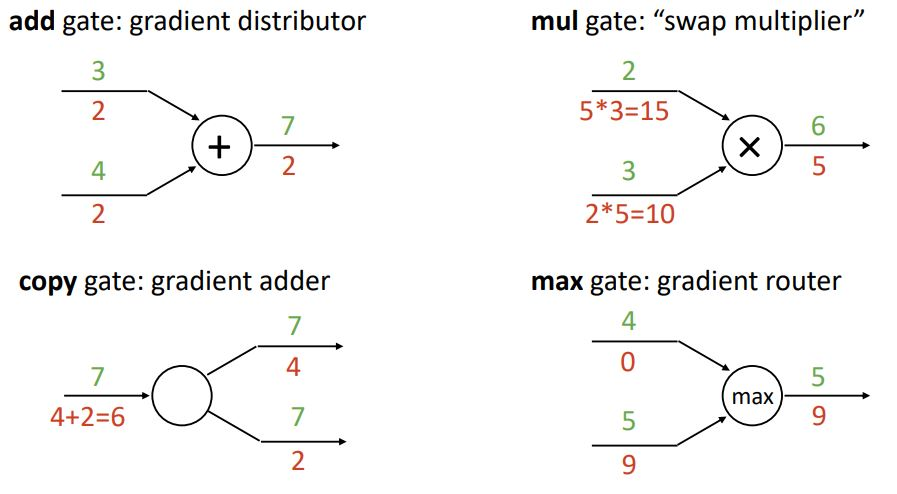
- Vectors in backpropagation
4-1) Vector derivative
*입력값과 출력값이 벡터인지 스칼라인지, 그리고 차원에 따라 도함수 형태를 보여줌.
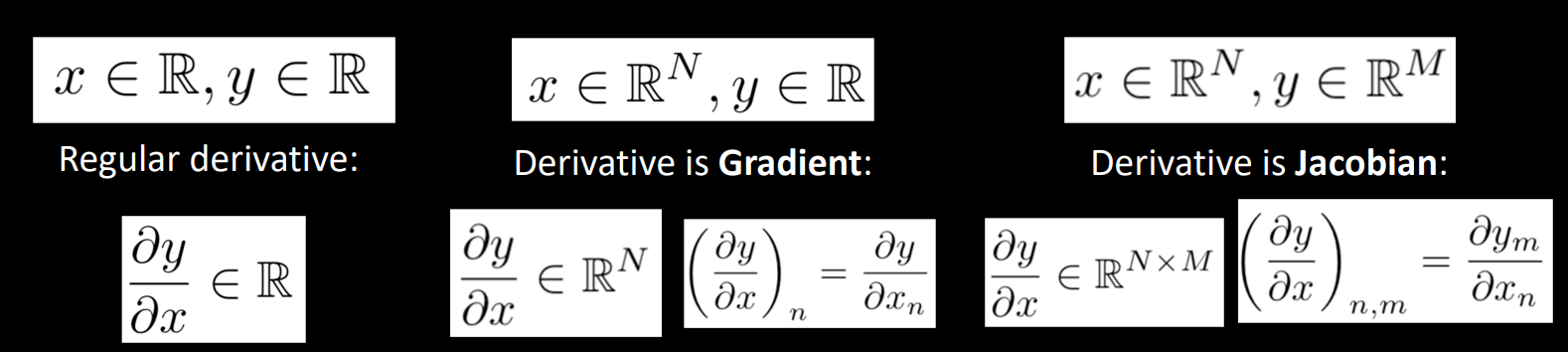
-
입력값과 출력값이 scalar이면, 미분값도 scalar
-
입력값이 n차원 vector이고 출력값이 scalar이면, 미분값은 n차원 vector이다.(gradient)
-
입력값이 n차원 vector이고 출력값이 m차원이면, 미분값은 n x m vector이다.(Jacobian matrix)
4-2) 그림으로 보는 backprop with vectors
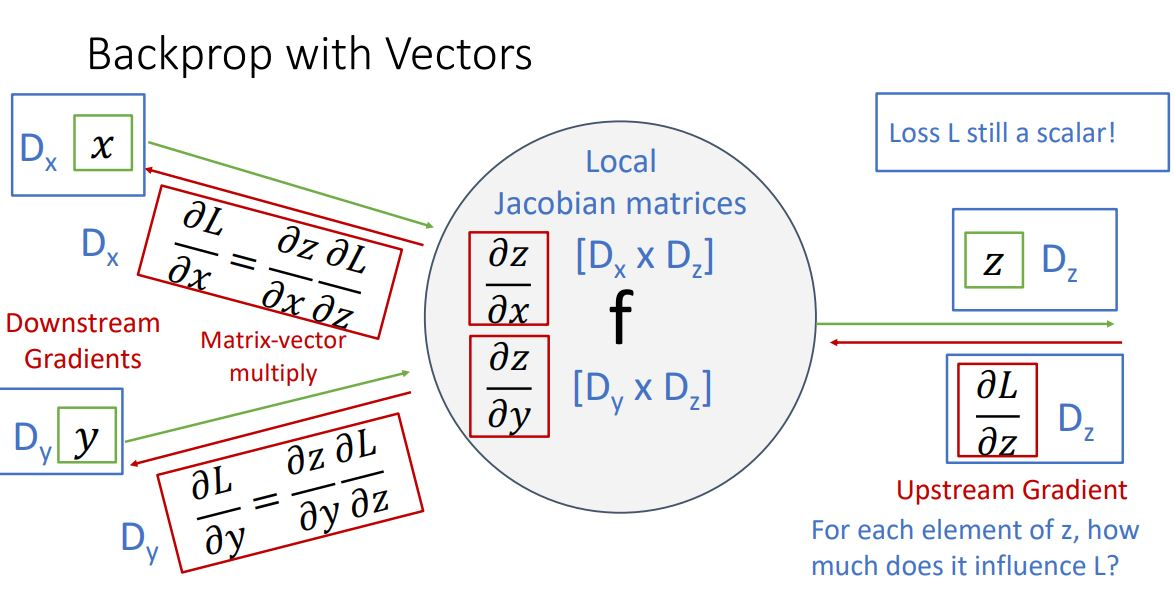
-
기본 조건
-
input x: x- dim vector
-
input y: y- dim vector
-
input z: z- dim vector
-
output: vector
-
loss: scalar
-
-
upstream gradient
- 방식: loss를 z-vector로 편미분
- 결과: z vector이 element의 loss에 영향을 얼마나 끼치는 지 나타낸다.
-
local gradient
- 방식: z- vector를 x-vector, y-vector로 편미분
- 결과:Jacobian matrix를 따른다.(x by z matrix, y by z matrix)
-
downstream gradient
- 방식: chain rule를 이용
- 과정: local gradient와 upstream gradient에 곱해줌
- 결과: x- vector이 나오게 된다.
- Matrices in backpropagation
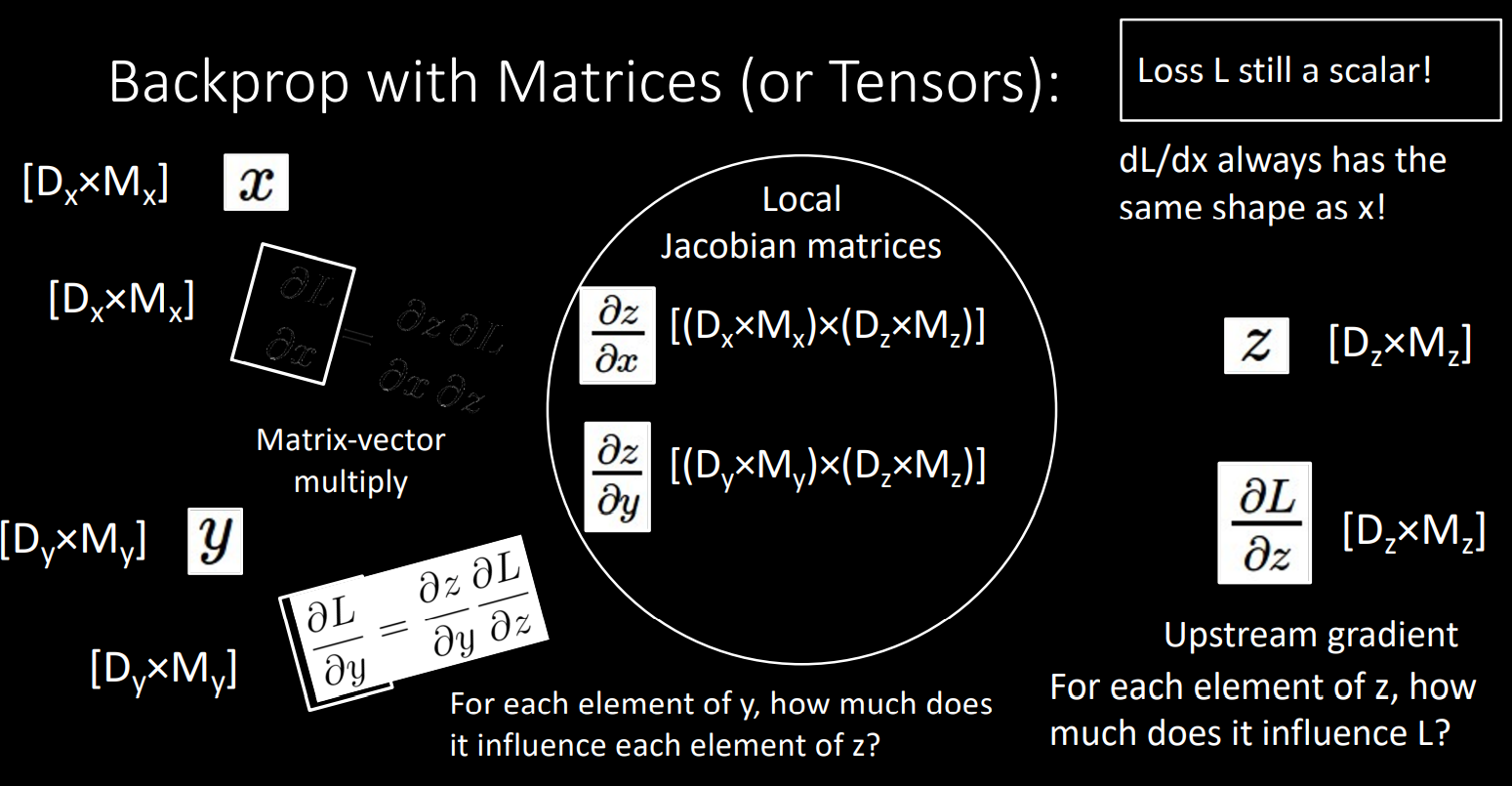
위의 과정과 같은 형태로 x,y,z가 matrix여도 backprop과정을 보입니다.
이상으로 기본적인 backpropagation에 대한 전반적인 내용을 배우게 되었답니다.
