Neural Networks

Blog목적

이번 블로그에서는 Neural Network의 정의 와 Linear classifier보다 왜 성능이 더 좋은지에 대해서 설명합니다. 그리고 추가적인 Optimization도 이야기를 해보도록합니다.

---

Neural Networks

신경망은 정보처리 시스템으로서 병렬, 분산 연결구조를 가지고 있으며, 외부로부터 받아들이는 입력에 대해 필요한 출력을 만듭니다.

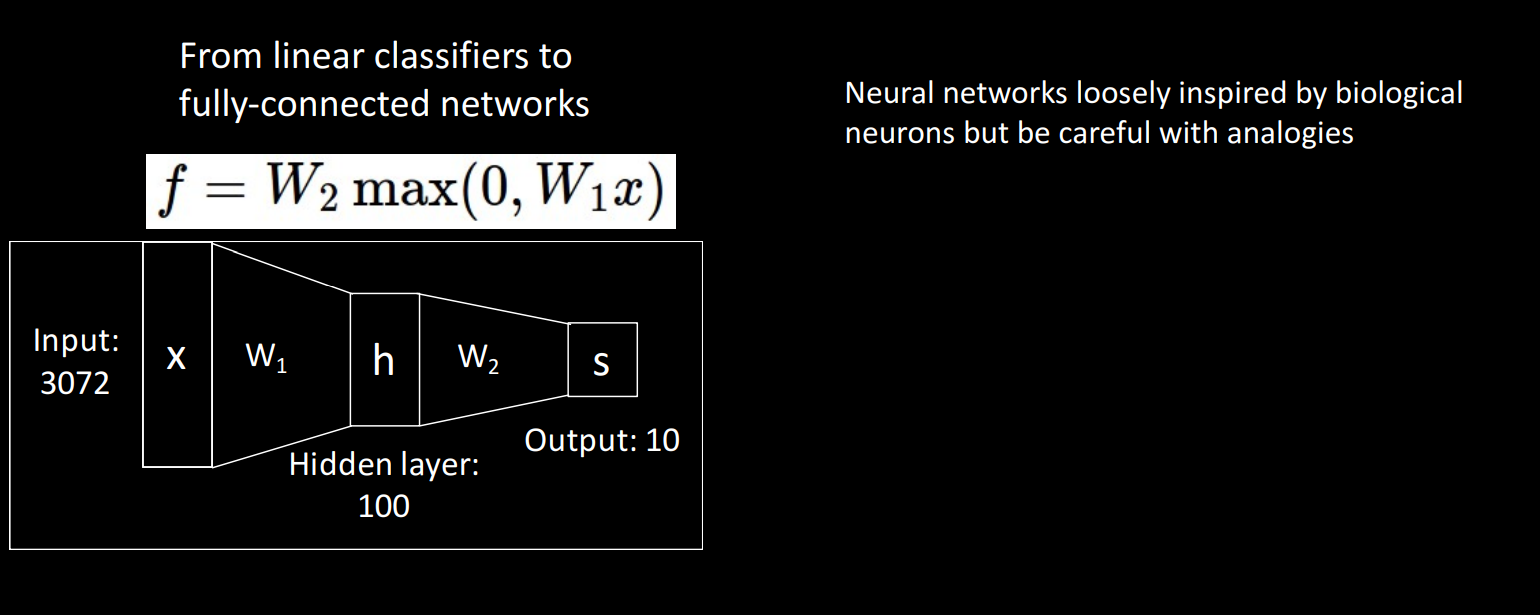
• Linear classifier을 쌓아서 구성된 것이고 bias는 생략합니다.

• 이전 레이어의 요소가 다음 레이어 요소에 영향을 끼칩니다.

• Called: Fully Connected Neural Network(FC NN) OR Multi Layer Perceptron(MLP)

• end to end 방식으로 구현이 가능하여 코드 구현이 쉬워지게 됩니다.

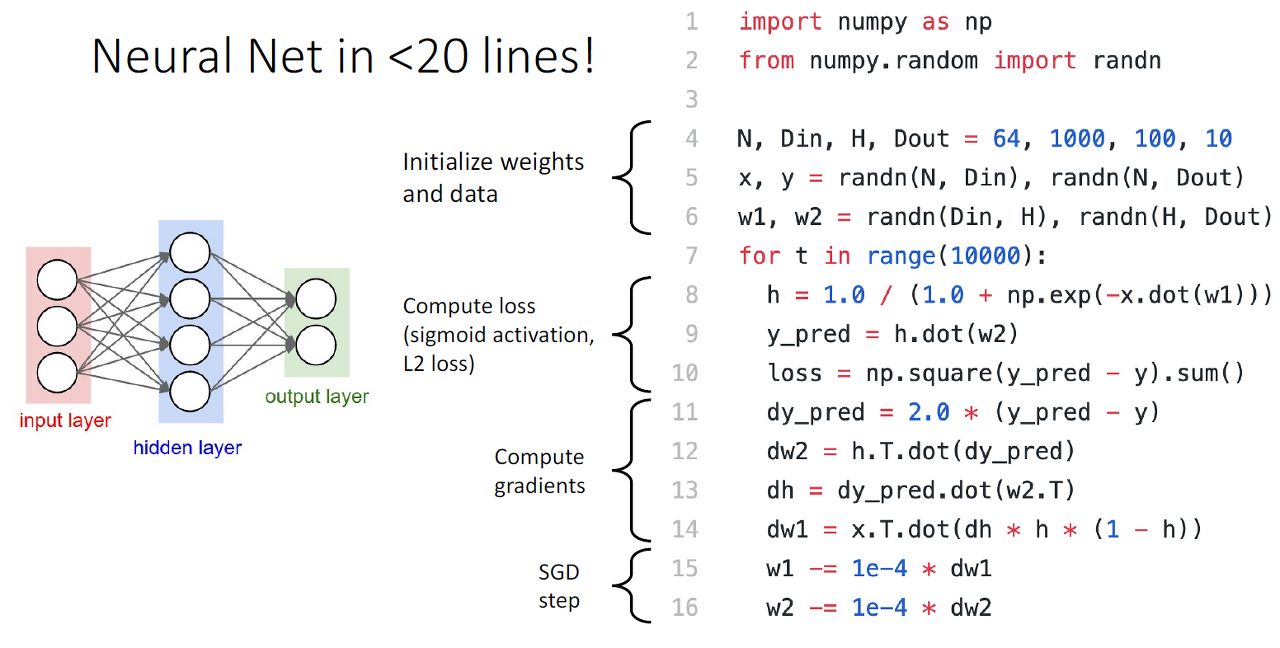
Linear classifier보다 NN이 성능이 좋은 이유

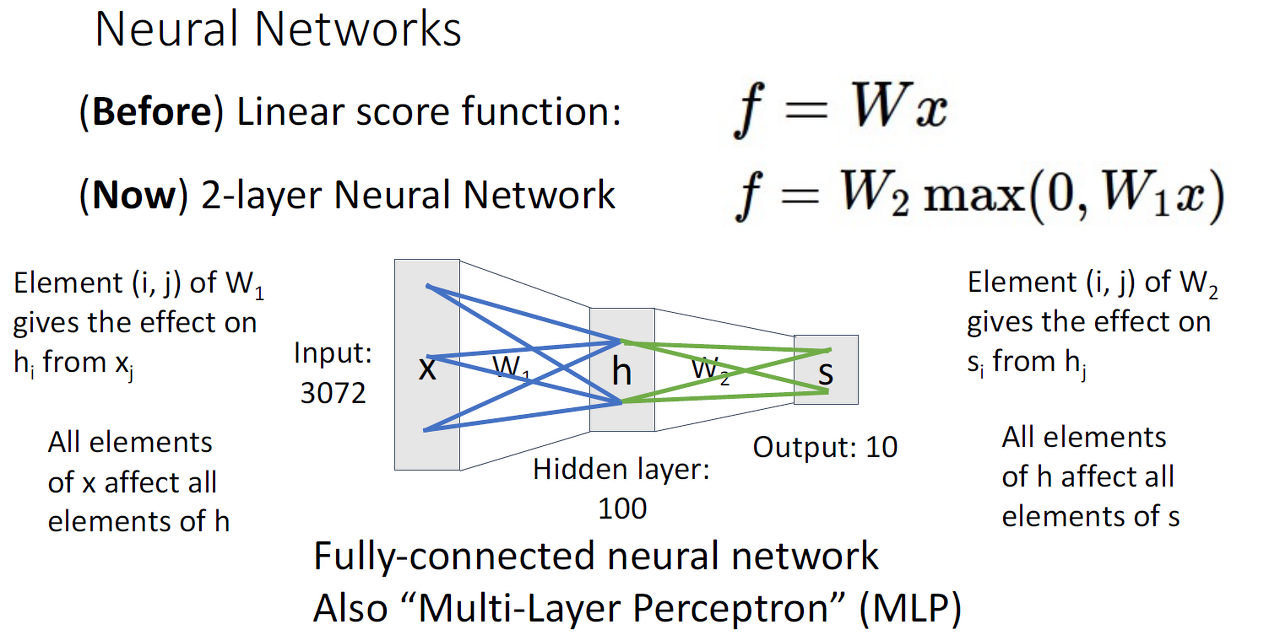
2-Layer Neural Network

• Distributed Representation: 어려 개의 탬플릿의 조합을 class로 표현하고 이게 가능한 이유는 MLP구조(이전 레이어의 정보 사용 가능)이기 때문입니다.

• 중복 정보를 가진 탬플릿을 만드는 경우도 있게 됩니다.

• Network Pruning: 중복 정보 탬플릿 해소

Space Warping

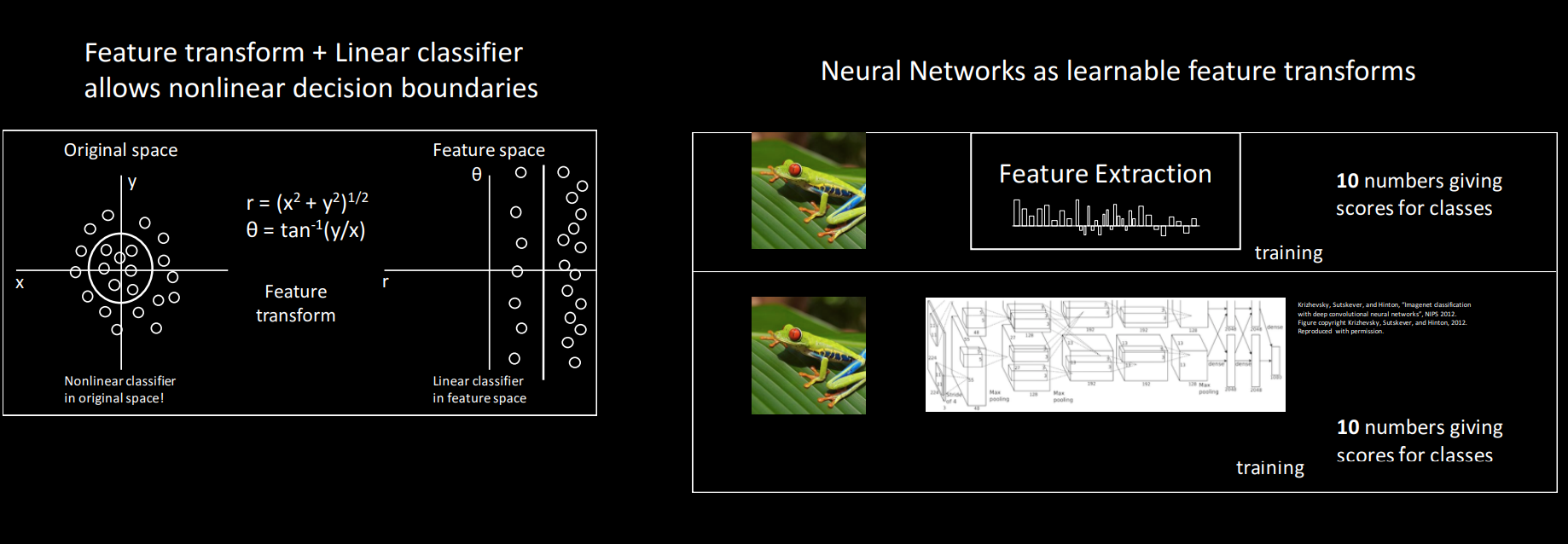
Linear classifier블로그에서 배운 Feature Transform방식은 사실 데이터를 완전히 분리하는데 어려움을 겪게 됩니다.

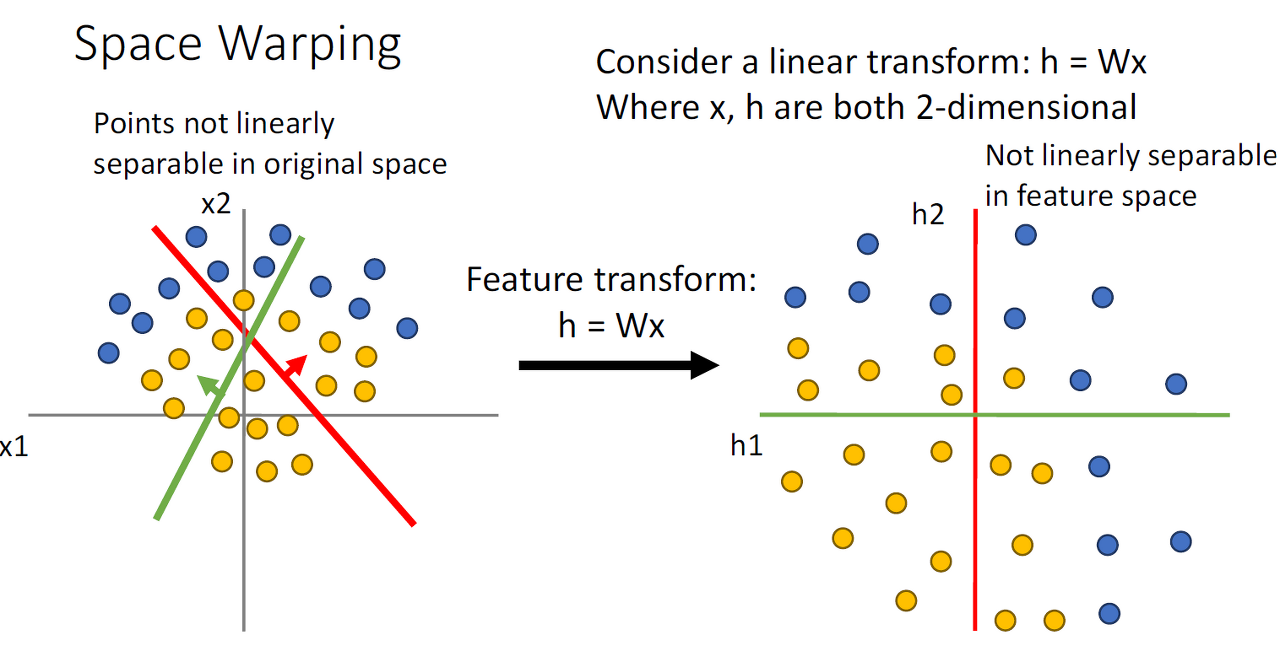
그러나, Neural Net에서 activation function을 사용하면 linear classifier가 데이터를 잘 분리하도록 바꿔주고 Non-Linear한 데이터도 잘 분리합니다.

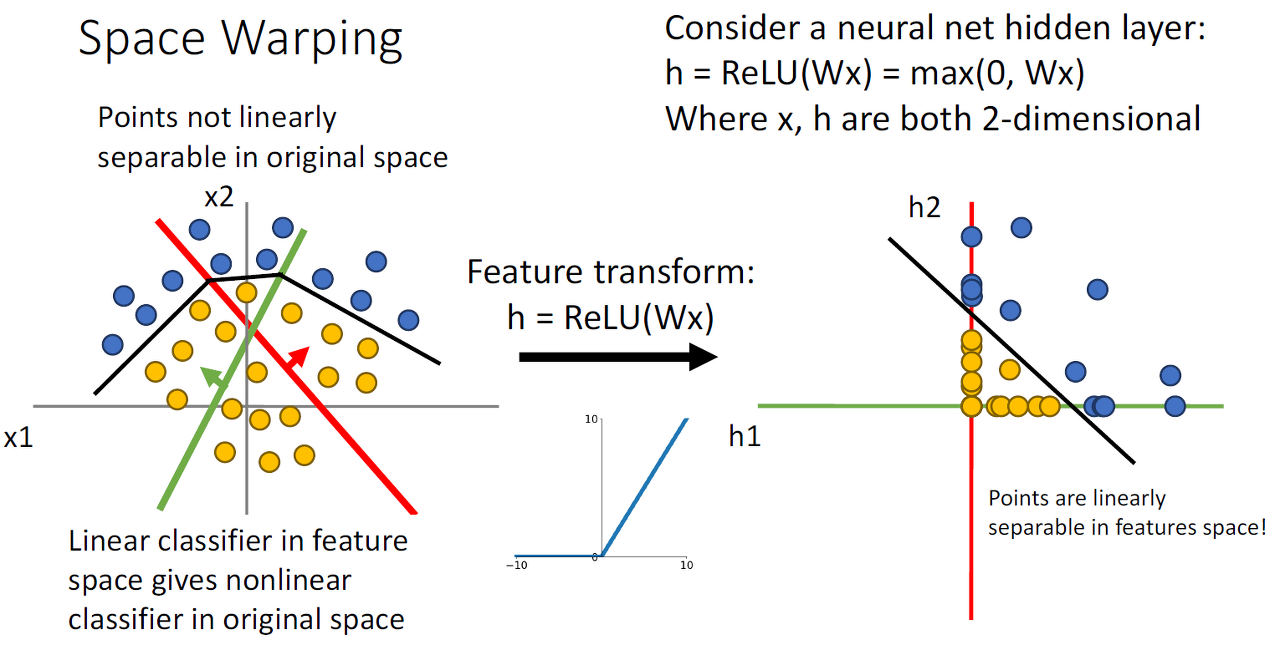
Universal Approximation

Universal Approximation을 알아보기 전에 간단하게 왜 은닉계층에서 유닛을 많이 사용하는지 알려드리려고 합니다.

그 이유는 유닛의 사용 수는 line을 많이 그어 구분하는 것과 동일하고, 적은 유닛을 사용해서 과적합 문제를 완화할 수 있게 됩니다. 허나 가장 좋은 방법은 regularizer을 이용하는 것입니다.

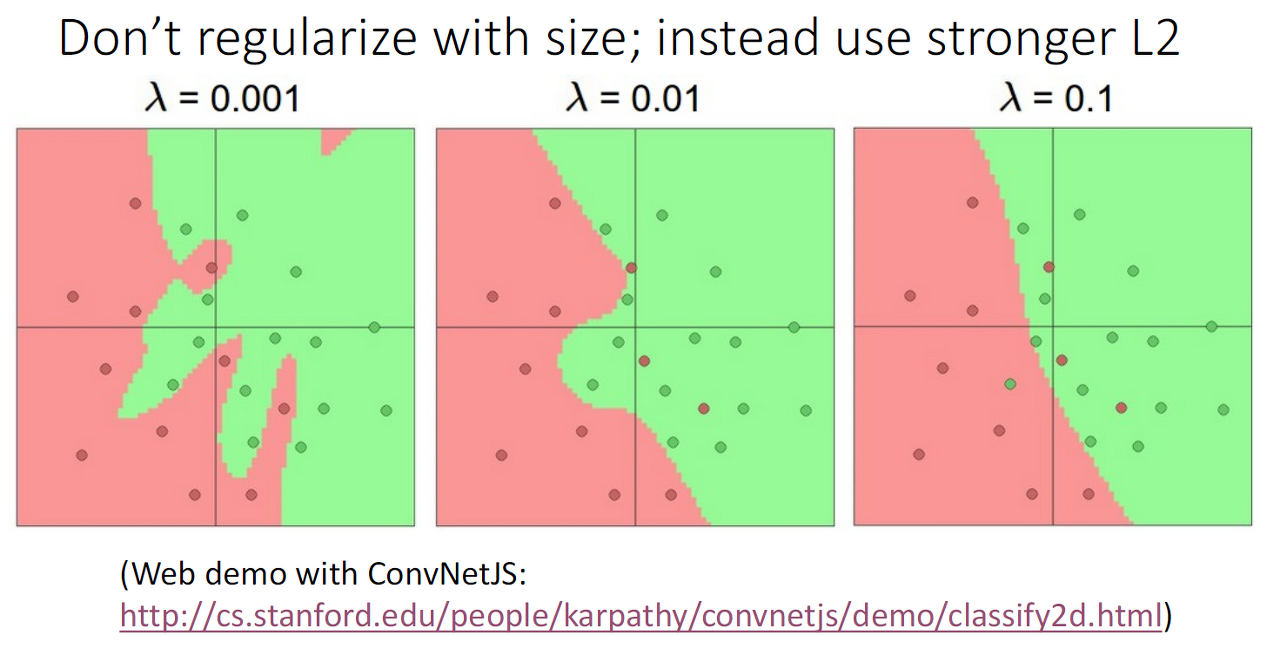
이제, Universal Approximation에 대해 알아보도록 합니다.

정의는 히든 레이어를 가진 모델은 어떤 함수든 근사하여 표현이 가능하다는 특징을 말합니다.

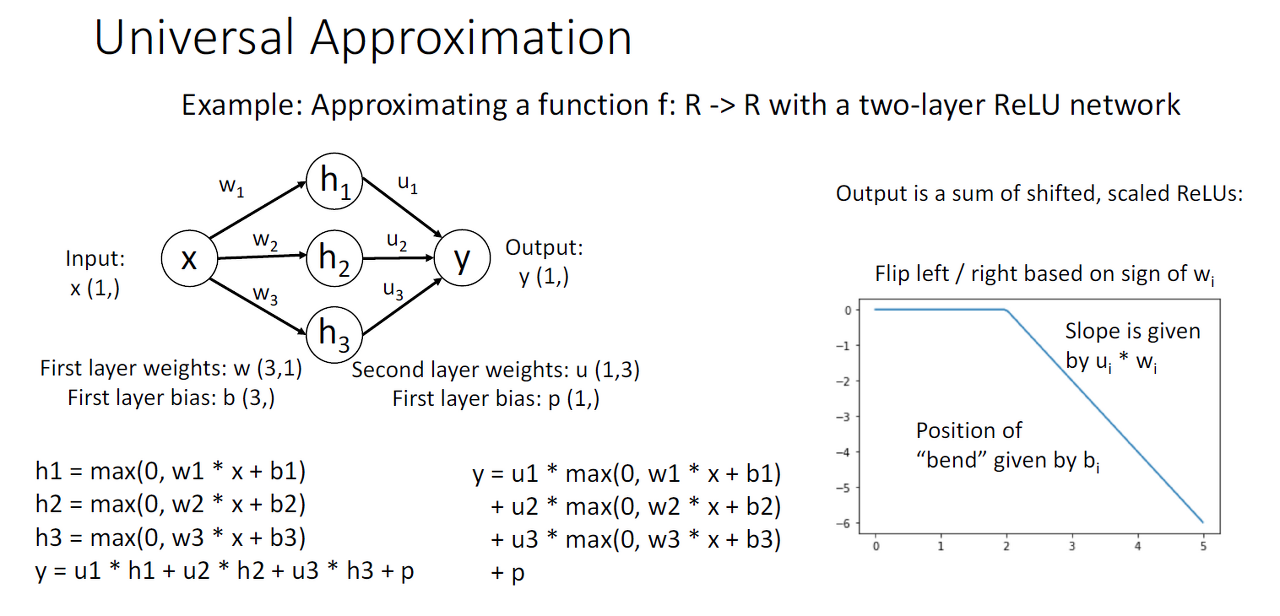
예를 들어, 위의 사진을 보면 2-layer relu network의 output인 Y는 shift와 scale이 된 relu의 합입니다.

그래서, relu를 모으면 bump function을 만들 수 있고 이를 통해서 어떤 함수든 근사할 수 있게 되어 2-layer neural network가 Universal Approximatino이 가능해집니다.

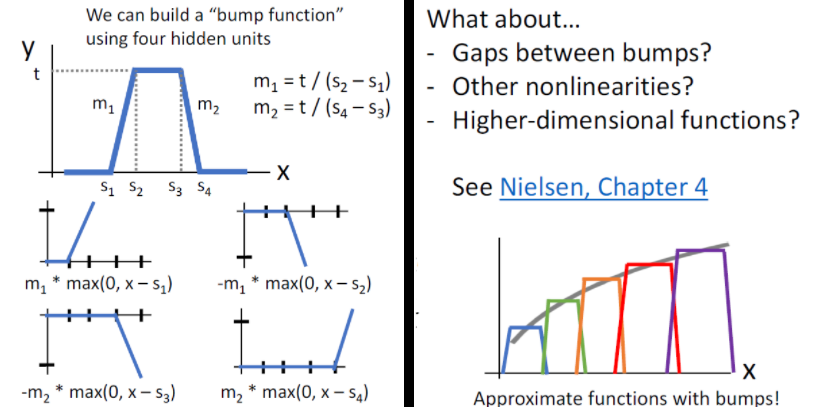
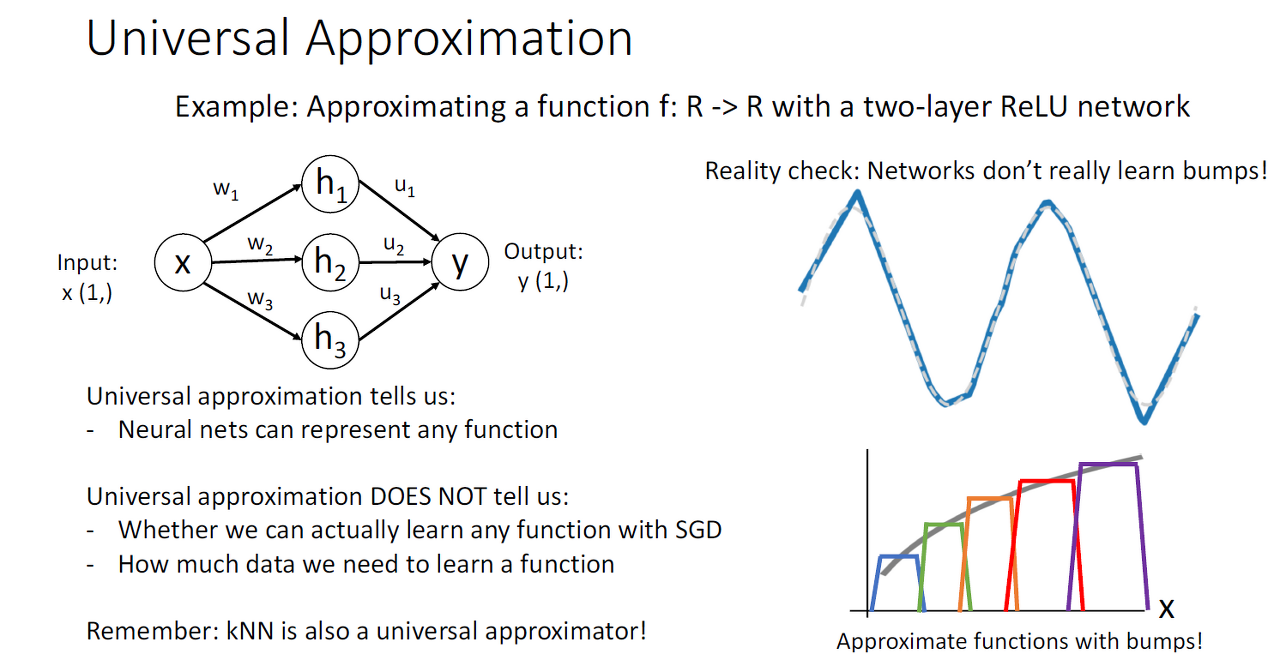
주의할 점 하나는 Aprroximzation이 가능한 것이지 NN이 Bump Function을 학습하는 것이라고 생각하면 안되고 어떤 함수든 표현이 가능한 것이지 얼마나 학습 데이터의 양과 구성 여부는 모릅니다.

그렇기에 NN이 최고 모델이라고 부르기는 어렵고 KNN 또한 Approximation이 가능합니다.

Deep Neural Networks(DNN)

DNN은 심층 신경망으로 불리는데 그 이유는 입력층(input layer)과 출력층(output layer) 사이에 여러 개의 은닉층(hidden layer)들로 이뤄진 인공신경망(Artificial Neural Network, ANN)이기 때문입니다.

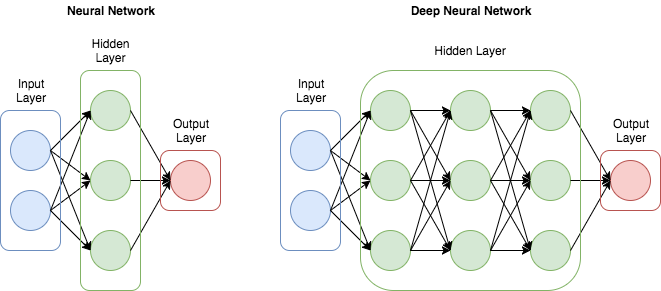
이미지 출처: 링크텍스트

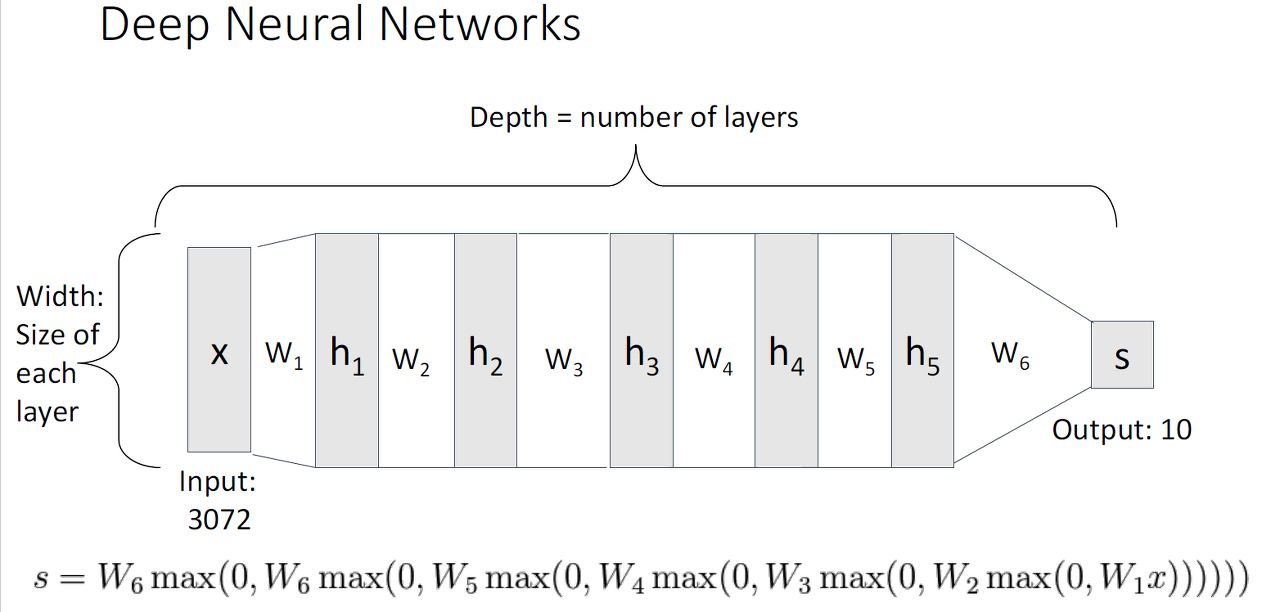
• Depth: layer의 수

• Width: layer의 크기

• max: activation function(ex:relu)이고 output 형성

Activation Functions

입력된 데이터의 가중 합을 출력 신호로 변환하는 함수로. 인공 신경망에서 이전 레이어에 대한 가중 합의 크기에 따라 활성 여부가 결정하고. 신경망의 목적에 따라, 혹은 레이어의 역할에 따라 선택적으로 적용합니다.

*2000년대는 sigmoid가 현재는 relu가 잘 쓰이는 추세입니다.

Optimization

Convex Functions

함수에서 두 점을 잇는 선분을 그을 때, 항상 두 점 사이에 위치한 점들이 모두 선분 아래에 위치하는 함수를 말합니다.

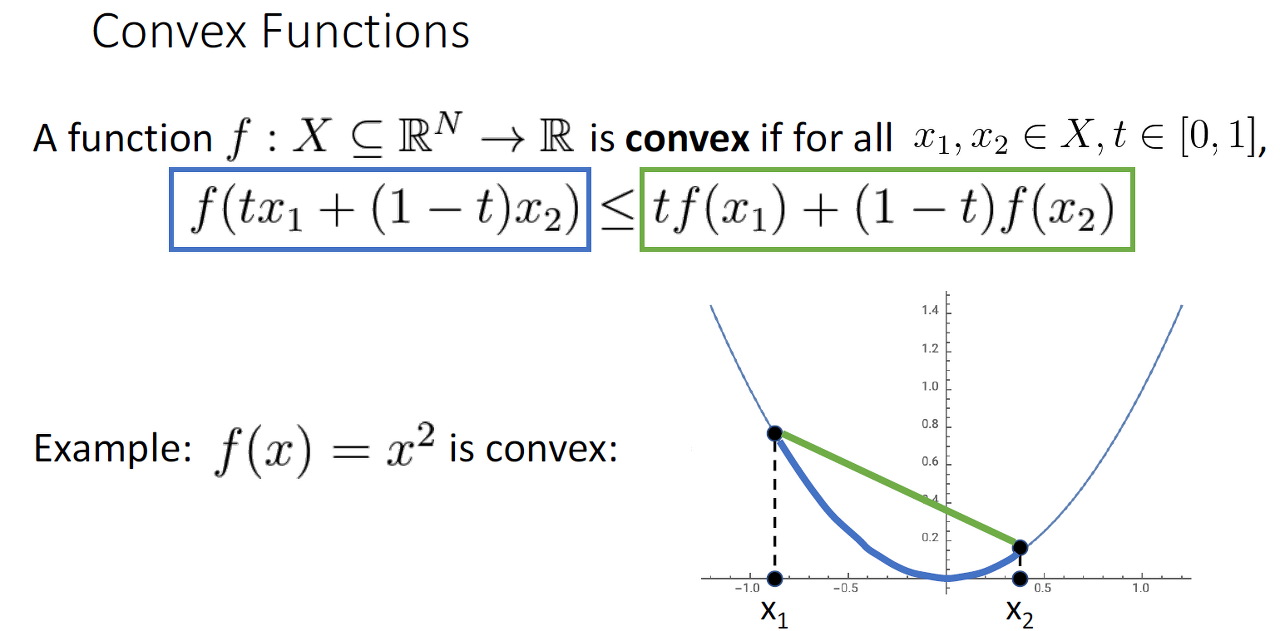
*고차원 공간

Convex Function은 bowl shape를 그리는 함수를 지칭하고 기울기를 따라가면 global minimum(전역 최소)에 도달할 수 있기에 초기화의 영향도 덜 합니다.

• Linear 모델 선호

Convex 함수가 항상 global minimum도달하는 게 이론적 보장이지만, 사실 NN에서는 이론적 근거가 없기에 간혹 linear 모델이 선호됩니다.

• Convex function확인 in NN

• 고차원의 LOSS에서 W vector의 1개 원소를 slice를 통해서 확인합니다.

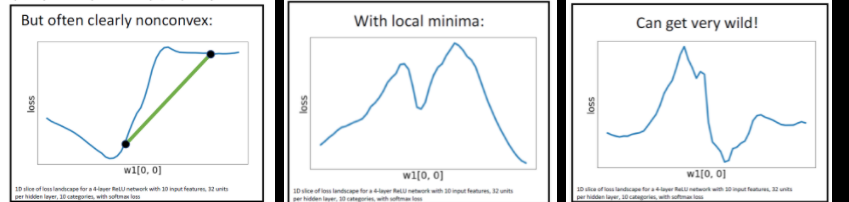
• 기타 조건

• Few or no guarantess about convergence
• Empirically it seems to work anyway
• Active area of research

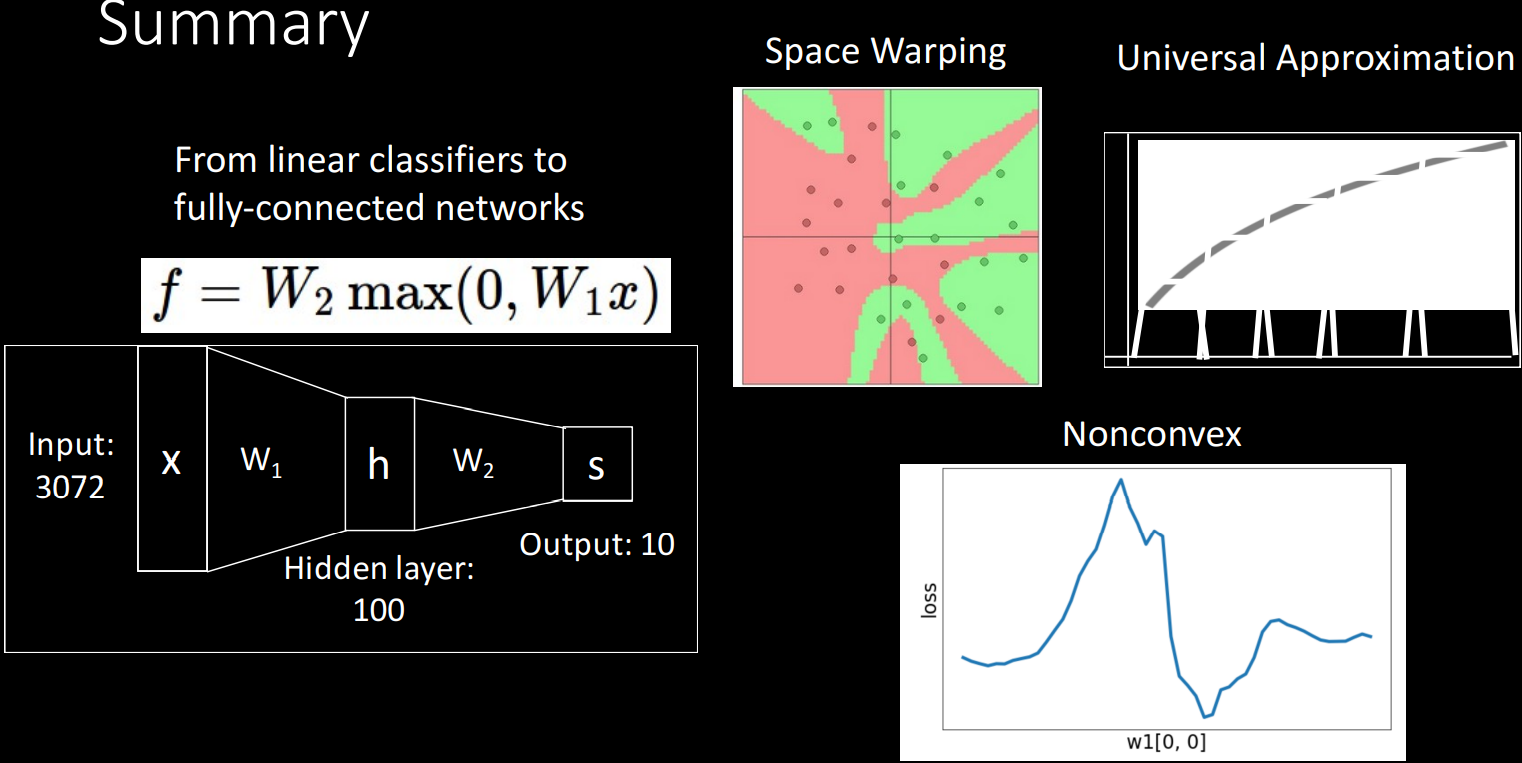
이미지로 보는 총 정리