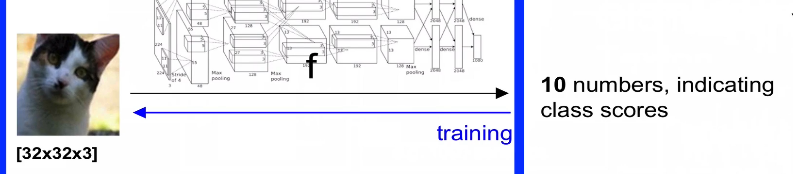
Loss function
Loss
-
정의: Loss is a function of weight
-
예시

-
f(x)을 통해서 각 score를 구함
-
(xi, yi) = (이미지, label)
-
score vector: s = f(xi, W)
Multiclass SVM loss(hingle loss)
-
정의: max()함수를 이용하여 0혹은 0 보다 큰 값을 추출하여 더함
-
식:
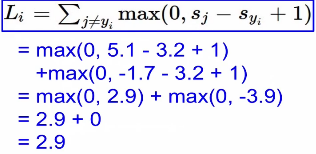
-
sj: 잘못된 레이블의 스코어
-
syi: 제대로된 레이블의 스코어
-
+1: safety margin
*What if the sum was instead over all classes?(including j= y_i)
 + max(0, sj -syi + 1)
+ max(0, sj -syi + 1)
*What if we used a mean instead of a sum here?
- loss 최소화 하는 파라미터를 구하는 게 목적이기 때문에 변화가 없다
*usually at initialization W are small numbers, so all s~=0.
what is the loss?
-
초기 loss = 클래스 -1
-
sanity check: 위의 식이 맞나 확인하는 작업
Softmax Classifier(Multinomial Logistic Regression)
- scores = unnormalized log probabilities of the classes.
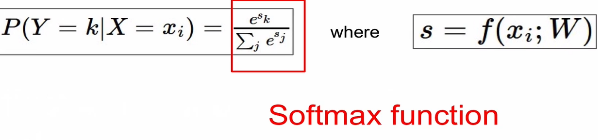
- To maximize the log likelihood or for a loss function , To minimize the negative log likelihood of correct class
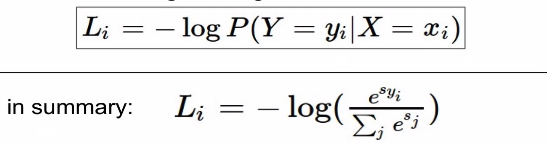
- Conclusion: Croos-entropy가 나오게 됨
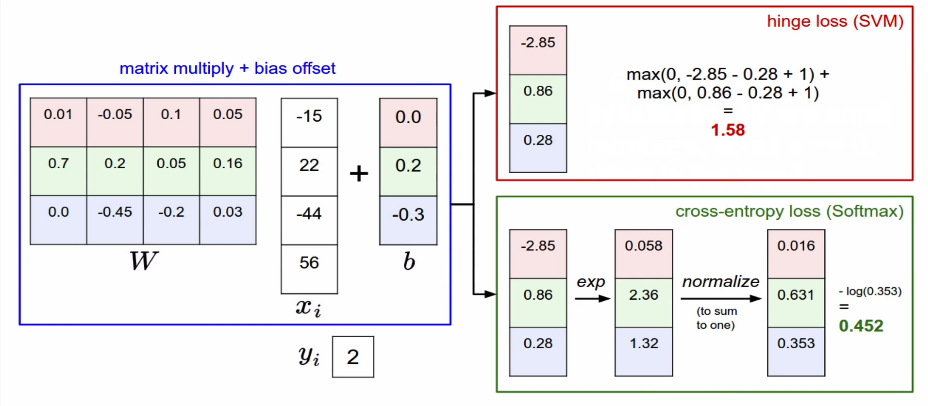
Softmax vs SVM
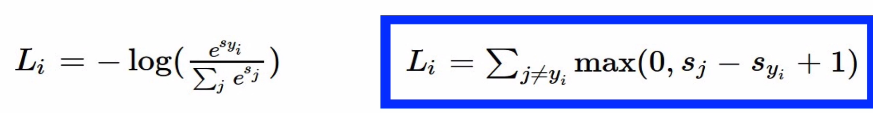
- score를 조정했을 때 loss가 어떻게 되나요
- SVM: loss값이 불변(둔감하여 값이 변하더라도 크게 영향 없음)
- Softmax: loss값이 변화(작은 변화에도 모든 값에 영향을 미치게 됨)
Weight Regularization
- regularization loss: data의 영향이 아닌 weight에만 영향을 받는다
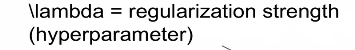
- lambda식 빼고 data loss
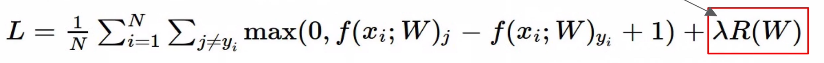
- data loss 와 regularization loss의 충돌로 인해서 data에 알맞고 가장 작은 weight를 구한다.
L2 regularization
-
식:
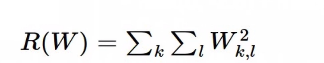
-
motivation
-
x = [1,1,1,1]
-
w1 = [1,0,0,0]
-
w2 = [0.25,0.25,0.25,0.25]
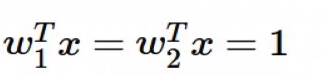
-
L1 regularization
- 식:
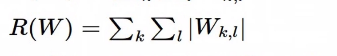
Elastic net
- 식:
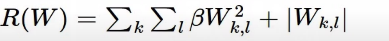
Optimization
Prievew
-
dataset :(x,y)
-
score function : s = f(x;W) =Wx
-
loss function:
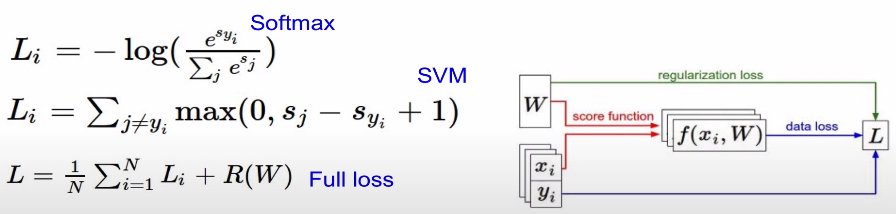
Strategy
- Random search
-
절대로 하면 안된다
-
accuaracy도 낮고 비효율적이다
-
Follow the slope(Gradient)

2-1. Numerical gradient
-
근사치이고 느리다
-
1차원인 경우에 함수 미분한 것이다.(수치적으로 경사를 구한다)
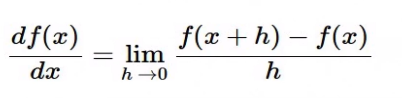
-
다차원인 경우 값이 아닌 벡터로 나온다
-
어리석은 방식이다
-
gradient check할 때 사용한다
2-2. Analtic gradient
-
빠르고 정확하다
-
error-prone
-
목표: weight 가 변할 때의 loss의 변화량
-
분석적으로 경사구하기(미분):
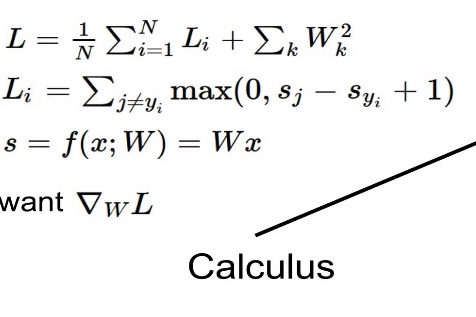
2-3. (full-batch) Gradient Descent
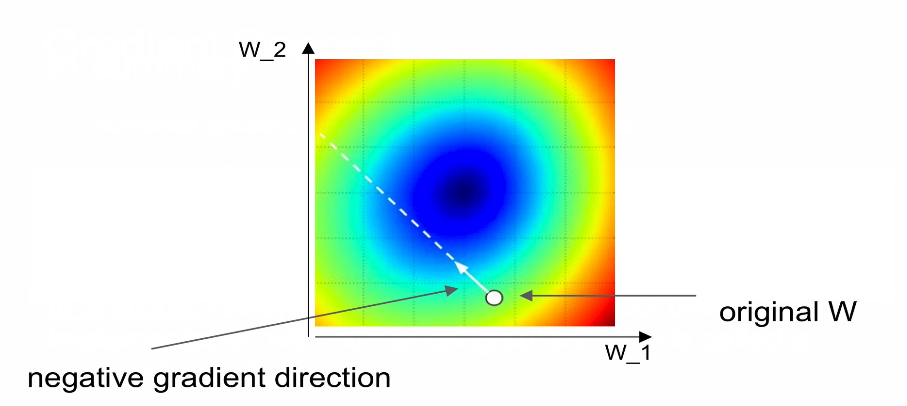

-
step_size: learning rate
-
마이너스: gradient 값만큼 weight를 감소시키기 때문이다.
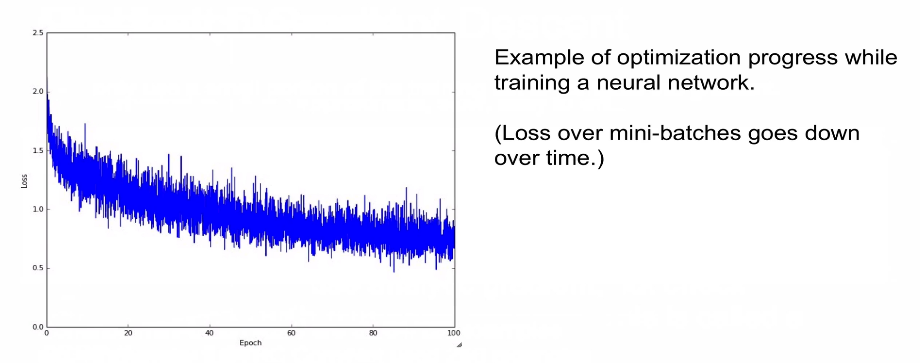
2-4. Mini-batch Gradient Descent
- 트레이닝 집합의 작은 부분을 사용하여 기울기 계산한다

-
흔한 배치 사이즈: 32/ 64/128
-
효과 (그래프)
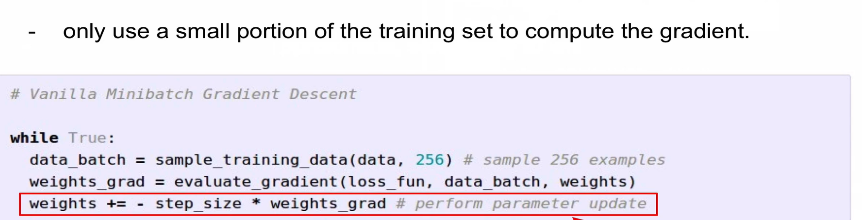
- Code
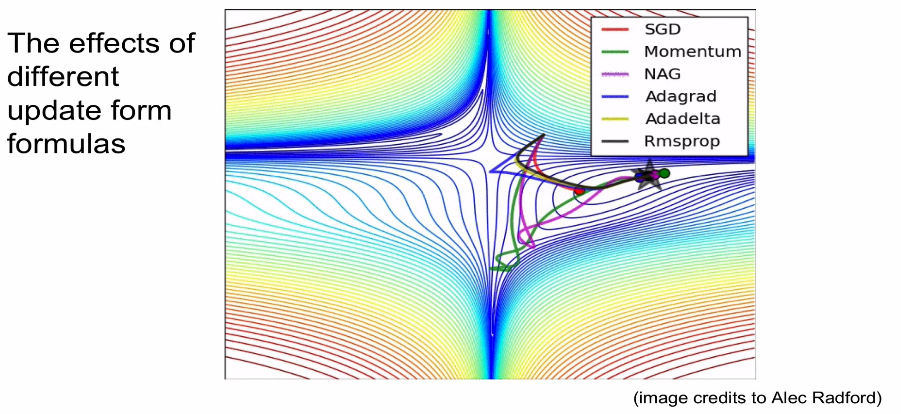
- 시각화
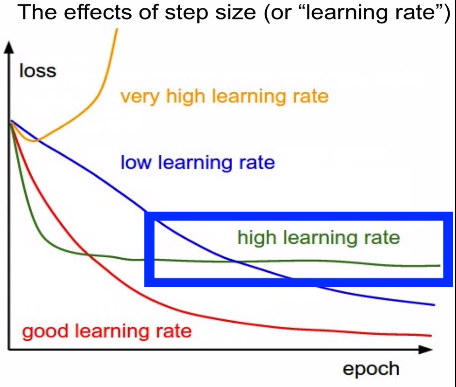
2-5. Learning rate 설정(어렵다)
- 방식은 높혔다가 점점 낮추는 방식으로 진행한다.
-
너무 큰 경우: diverge/ explode
-
큰 경우: loss=0으로 수렴이 불가한다
-
너무 작은 경우: slow convergence
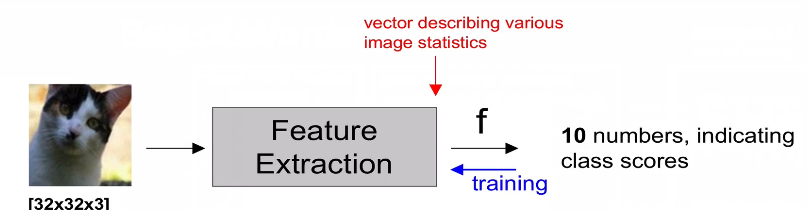
Image Features
- Features 추출 후 compact nation 실행 그 다음에 Linear classifier 적용
Feature 추출 방식
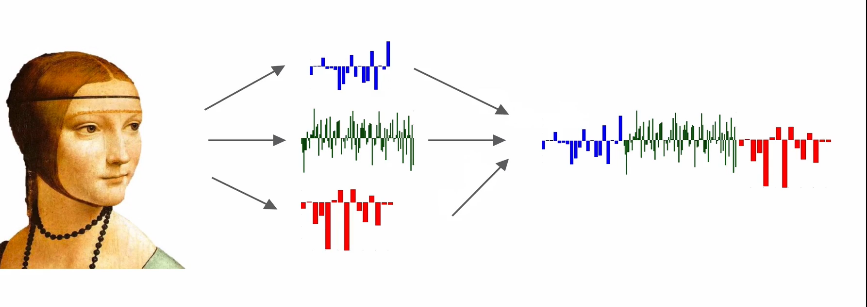
- Color (Hue) Histogram
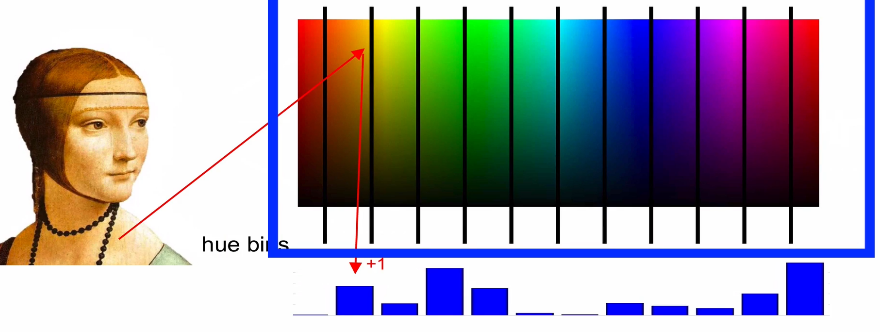
- 각각의 bin에 속한 것들이 몇 개 있는 센다
- HOG/SIFT features

-
edge방향: features
-
유사방식: GIST, LBP, Texton, SSIM
- Bag of Words
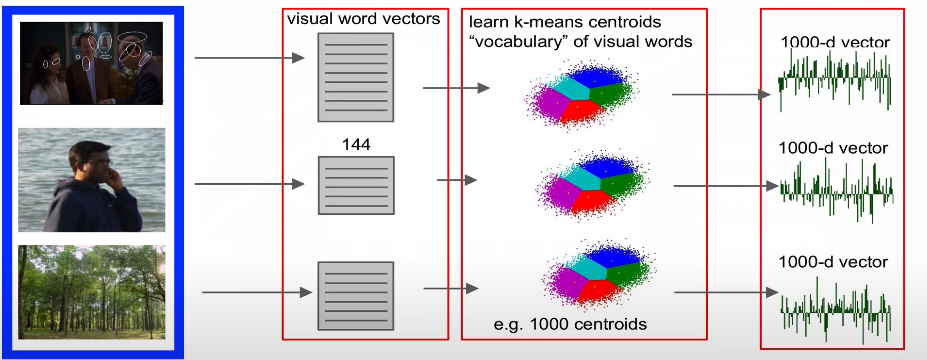
3.1 위의 처리과정
- 이미지의 여러 지점 파악
-작은 local 패치들을 벡터화
-
하나의 사전화를 한다
-
테스트할 이미지 픽쳐 벡터를 사전에서 찾는다
-
픽처 벡터 추출 후 계산
-
linear classifier 적용
3.2 이미지 도식화
- 전통적인 방식
- New