Merge Sort

Merge Sort(분할 정복 알고리즘)

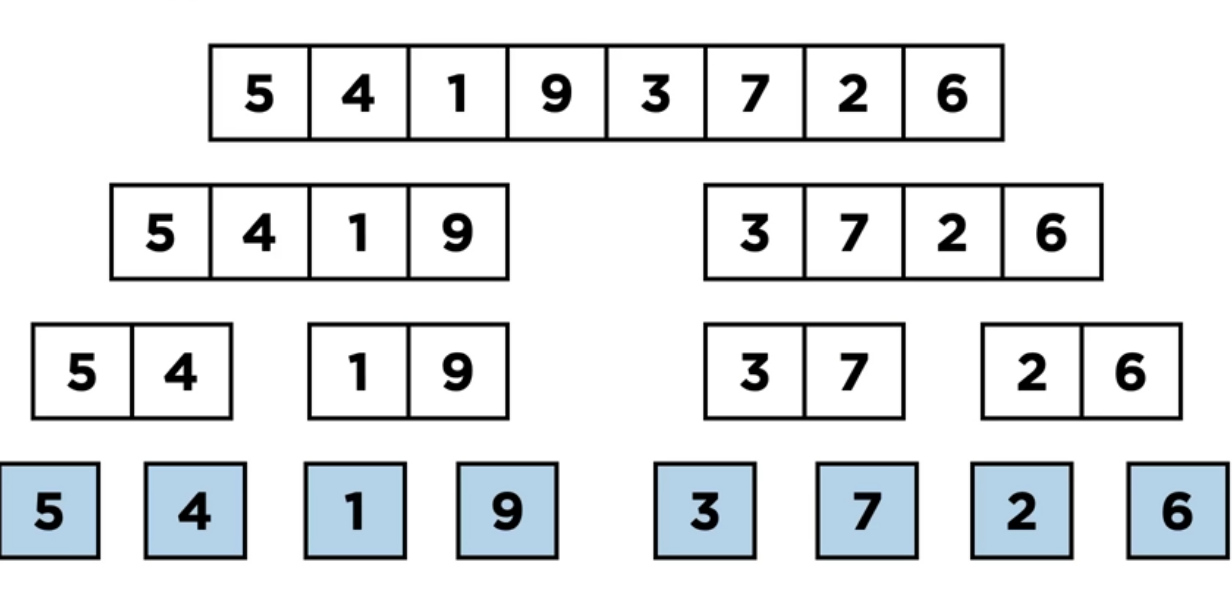
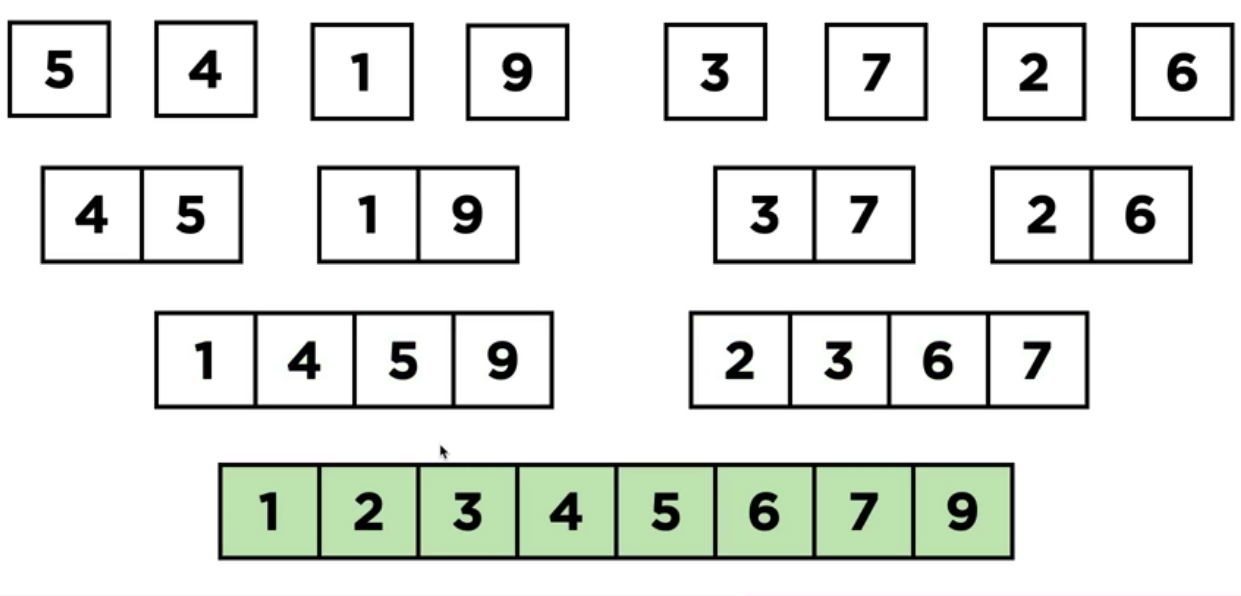
하나의 리스트를 두 개의 균등한 크기의 리스트로 분할을 한 후에 부분 리스트를 합치면서 정렬을 합니다.

그래서, 전체가 정렬이 되게 하는 방식입니다.

주로 재귀함수에서 쓰입니다.

시간복잡도는 O(NlogN)

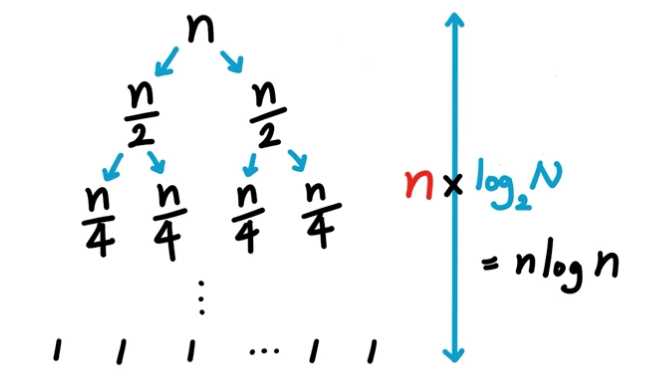
*예시

code

def merge_sort(arr): #merge정렬
    if len(arr) <= 1: # 길이가 1보다 작다면 
        return #그냥 return
 
    #나누기
    mid = len(arr)//2 #중간 부분
    left = arr[:mid]#분할된 인쪽 리스트
    right = arr[mid:] #분할된 오른쪽 리스트

    merge_sort(left) #왼쪽 리스트에 적용
    merge_sort(right) #오른쪽 리스트에 적용

    #정복

    i = 0 #left idx
    j = 0 #right idx
    k = 0 # arr idx

    while i < len(left) and j < len(right): #i와 j가 커지기 전까지 계속 실행
        if left[i] <= right[j]: # 오른쪽이 더 많다면
            arr[k] = left[i] #인덱스 부분과 왼쪽이 같다
            i +=1 #1증가
        else:
            arr[k] = right[j] #인덱스 부분과 오른쪽이 같다면
            j += 1#1증가
        k +=1 #인덱스 1 증가
    
#전체 정렬이 되고 왼쪽 오른쪽 부분만 남은 상태

    while i < len(left): # 왼쪽보다 클 뗴끼지하기
        arr[k] = left[i] # 같다
        i += 1 #왼쪽 리스트 1 증가
        k += 1 #인덱스 증가

    while j < len(right): # 오른쪽 클때까지
        arr[k] = right[j] #같다
        j += 1 #오른쪽 인덱스 증가
        k += 1  # 인덱스 증가
if __name__ == "__main__": #main.py
    arr = [9,1,6,3,7,2,8,4,5,0] #배열
    merge_sort(arr) #병합정렬 적용
    print(arr) #결과값
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]