베르누이분포

베르누이 분포

intro

비모수적 기법

모집단의 확률 분포에 대한 특별한 가정없이, 평균과 분산이라는 지표를 추정

모수적 기법

모집단의 성질에 따라 확률 분포의 형태인지를 미리 가정한 후, 기댓값 혹은 분산을 결정하는 소수의 파라미터 추정

정의와 특징

• 가장 기본적인 이산형 확률 분포

• 변수의 확률값이 동일

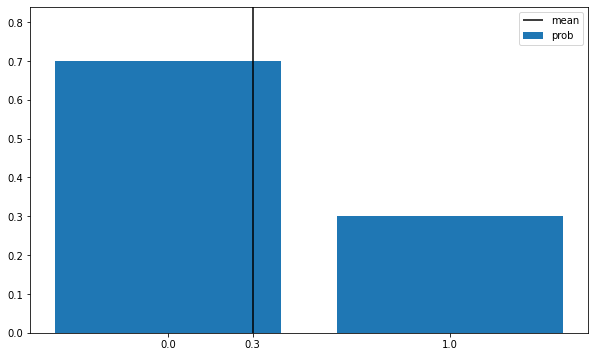
• 성공/실패와 같이 두 가지에 대한 분포로 성공확률p, 실패확률 1-p가 있는 분포

• 취할 수 있는 값은 0(실패) 혹은 1(성공)

• 1과 0이 나올 확률을 각각 더하면 1이 되어야하므로, 그 확률을 각각 p와 1-p로 정의

• 0<=p<=1이라는 조건 만족(확률의 성질에 따라)

• 베르누이 분포를 Bern(p)로 표기

• 확률함수 공식

  • f(x) = p^x(1-p)^(1-x) {x is 0 or 1}

  • f(x) = 0 (otherwise)

• X ~ Bern(p)

  • E(X) = p

  • V(x) = p(1-p)

Code

def Bern(p):
    x_set = np.array([0,1])
    def f(x):
        if x in x_set:
            return p ** x * (1-p) **(1-x)
        else:
            return 0
    return x_set,f

p=0.3
X = Bern(p)

plot_prob(X)