이항분포

이항 분포(Binomial Distribution)

• 성공 확률이 p인 베르누이 시행을 n번 했을 때의 성공 횟수를 나타내는 분포

• 취할 수 있는 값: [0,1,...,n]

• 파라미터: 성공확률 p, 시행 횟수 n

• 0<=p<=1, n은 1이상인 정수라는 조건을 만족해야한다

• Bin(n,p)로 표기

• 확률함수 공식

  • f(x) = (n x)p^x(1-p)^(n-x) {x is in [0,1,..n]}

  • f(x) = 0 (otherwise)

• 이항 분포 기댓값과 분산

  • E(X) =np

  • V(X) = np(1-p)

Code

from scipy.special import comb # comb함수를 통해서 (n x)구현

def Bin(n,p):
    x_set = np.arange(n+1)
    def f(x):
        if x in x_set:
            return comb(n,x) * p**x * (1-p)**(n-x)
        else:
            return 0
    return x_set, f

    
n = 10
p = 0.3
X = Bin(n,p)

check_prob(X)

plot_prob(X)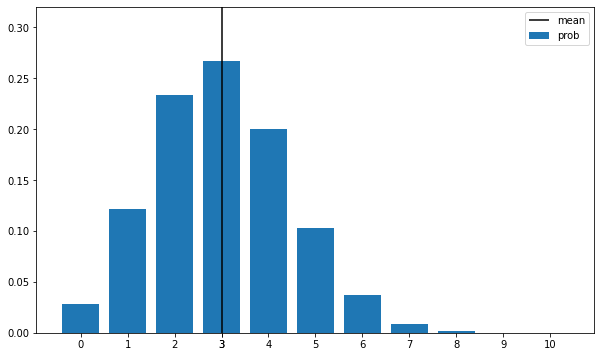

fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(111)

x_set = np.arange(n+1)
for p, ls in zip([0.3, 0.5, 0.7],linestyles ):
    rv = stats.binom(n, p)
    ax.plot(x_set, rv.pmf(x_set),
            label=f'p:{p}', ls=ls, color='gray')
ax.set_xticks(x_set)
ax.legend()

plt.show()