Q11) 중심극한 정리는 왜 유용한가?
Intro
정규분포는 중앙치에 사례 수가 모여있는 형태입니다.
정의
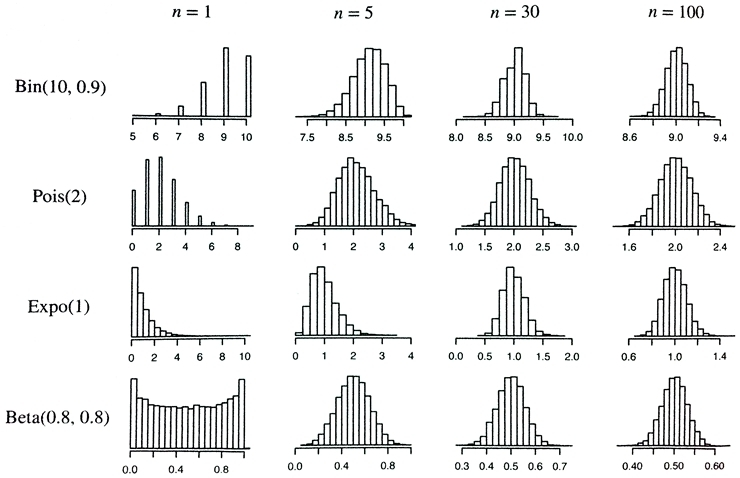
동일한 확률 분포를 가지면서 독립 확률인 n개의 확률변수의 평균 분포가 점점 커지면 정규 분포에 가까워집니다.
*이미지로 보는 중심극한 정리 모습
개인적인 질문) 왜 이게 중요할까?
이유: 중심극한정리로 인해서 모집단의 형태에 상관없이 표본 평균의 분포가 정규분포를 따르게 되고 이로 인해 Z깂을 통한 확률값을 구할 수 있게 됩니다.
다시 말하자면, 모집단의 형태가 난해해도 수학적 확률 추정을 할 수 있게 된 것입니다.
Q12)엔트로피와 정보이득란?
정의1
엔트로피: 주어진 데이터의 혼잡도를 바탕으로 데이터가 어떤 클래스에 속할 확률에 대한 기댓값으로 데이터가 서로 다른 클래스에 속하면 높고, 그렇지 않다면 낮습니다.
즉, 데이터들이 클래스에 속할 확률의 차이가 크면 엔트로피가 낮고 각 클래스에 속할 확률이 비슷하면 엔트로피는 높습니다.
다시 말하면, 확률 분포가 가지는 차이를 하나의 숫자로 표현한 것이 엔트로피입니다.
공식
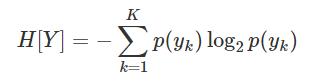
코드
plt.figure(figsize=(9, 3))
plt.subplot(131)
plt.bar([0, 1], [0.5, 0.5])
plt.xticks([0, 1], ["Y=0", "Y=1"])
plt.ylim(0, 1.1)
plt.title("$Y_1$")
plt.subplot(132)
plt.bar([0, 1], [0.8, 0.2])
plt.xticks([0, 1], ["Y=0", "Y=1"])
plt.ylim(0, 1.1)
plt.title("$Y_2$")
plt.subplot(133)
plt.bar([0, 1], [1.0, 0.0])
plt.xticks([0, 1], ["Y=0", "Y=1"])
plt.ylim(0, 1.1)
plt.title("$Y_3$")
plt.tight_layout()
plt.show()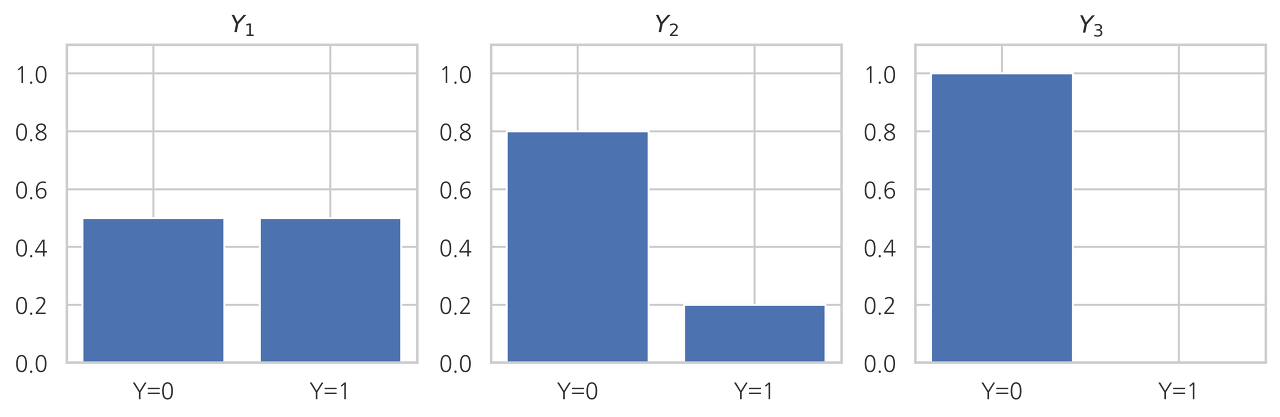
정의2
정보이득: 데이터가 어떤 클래스에 속할 확률이 커짐에 따라서 정보를 잘 얻게 되는 것으로, 감소되는 엔트로피 양을 의미합니다.
공식
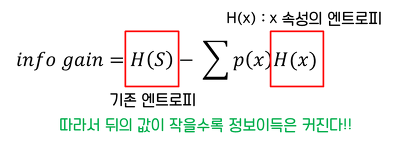
개인적인 질문) 정보 이득의 활용
의사 결정 트리에서 가지를 칠 때 이 값을 이용해서 사용이 됩니다.
어떤 데이터를 두 집합으로 나누었을 때 두 집합의 정보이득이 크도록, 엔트로피는 작아지도록 분할한다
그림으로 보는 예시
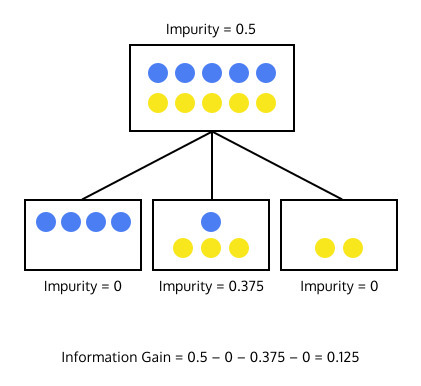
Q13) Likelihood 와 Probability의 차이
확률(Probability)은 어떤 시행에서 특정 결과가 나올 가능성으로 시행 전 모든 경우의 수의 가능성은 정해져 있고 총합은 1이다.

가능도(Likelihood)은 어떤 시행을 충분히 수행 후 결과를 토대로 경우의 수가 나타낼 가능성을 도출하는 것이기에 추론에 가깝습니다. 그래서, 가능성의 합이 1이 안될 수도 있습니다.
왜냐하면, 확률 분포의 모수가, 어떤 확률변수의 표집값과 일관되는 정도를 나타내는 값이다.
구체적으로, 주어진 표집값에 대한 모수의 가능도는 이 모수를 따르는 분포가 주어진 관측값에 대하여 부여하는 확률입니다.
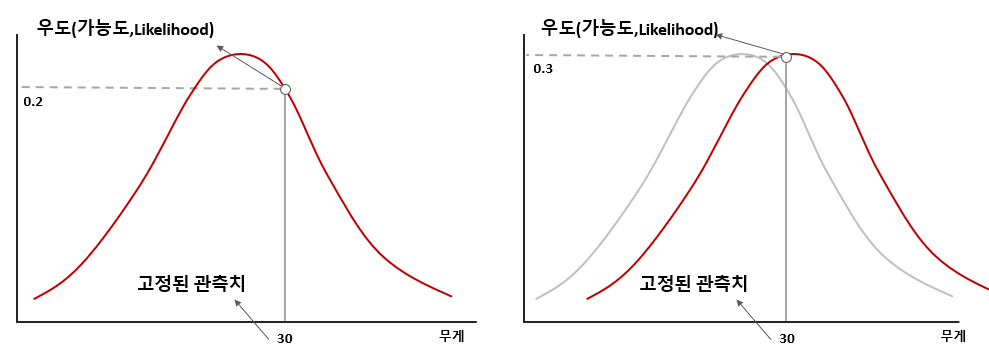
정리하자면, PDF(Probability density function)는 확률변수를 변수로 보기에 총합은 1이지만 likelihood function에서 분포의 모수를 변수로 보기 때문에 총합이 1이 되지 않습니다.
Q14) bootstrap의 의미
Intro
복원추출
확률을 구할 때, 추출했던 것을 원래대로 돌려놓고 다시 추출하는 방법
정의
부트스트랩은 가설검증을 하거나 metric을 계산하기 전에 random sampling을 적용하는 방법이다. 모수의 분포를 추정하는 방법 중 하나는, 현재 가진 표본에서 추가적으로 표본을 복원추출하고 각 표본에 대한 통계량을 다시 계산하는 것이다.
부트스트랩이 여기에 해당하며, 여러번의 무작위 추출을 통해, 평균의 신뢰구간을 구할 수 있다.
이러한 이유로 200개로만 통계량을 구하는 것이 아니라 200개를 기준으로 복원 추출하여 새로운 통계량을 구하는 것을 예시로 들 수 있습니다.
개인적인 질문) 머신러닝에서 부트스트랩의 의미는 무엇일까?
랜덤 샘플링을 통해 학습 데이터를 늘리는 방법
여러 모델을 학습시켜 추론 결과의 평균을 사용하는 방법(=앙상블)