간단 코드: 링크텍스트
프로젝트 : 링크텍스트
시계열 예측
Preview
-
정의: 시간 순서대로 발생한 데이터의 수열
-
수식:
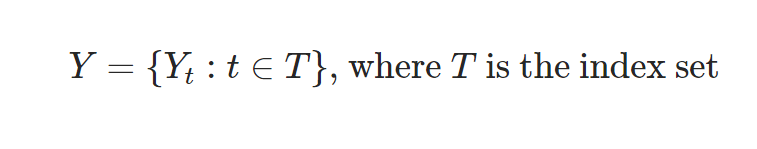
-
전제 조건:
- 과거의 데이터에 일정한 패턴 발견
- 과거의 패턴은 미래에도 동일하게 반복
- 즉, 안정적 데이터에 대해서만 미래 예측이 가능
- 시계열 데이터의 통계적 특성이 변하지 않는다.
Stationary
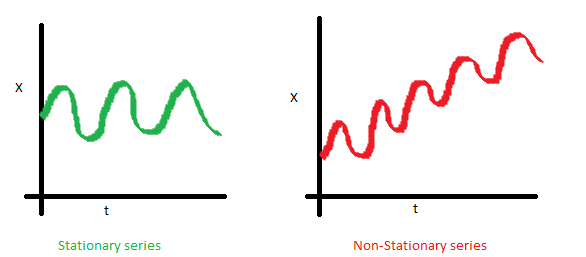
-
일정 조건
- 평균
- 분산
- 공분산
-
Covariance
- 변수의 단위 크기에 영향을 받는다
- 값자체가 두 변수 간의 상관성 대표 안함
- 두 확률 변수가 독립이면 0 값을 갖는다.
- 안정적인 시계열에서 시차 h가 같다면 데이터의 상관성이 동일 주기를 나타냄
- t에 무관해야한다.
- Correlation: Covariance를 Normalize하여 [-1,1] 사이의 값으로 표현되도록 보정, 두 확률 변수가 독립일 경우 0의 값을 갖는다
Stationary 여부 체크
Augmented Dickey-Fuller Test
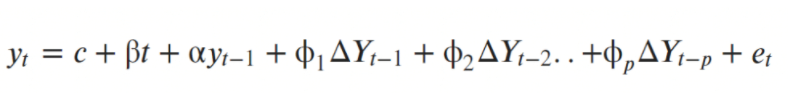
-
주어진 시계열 데이터의 안정성이 없다는 귀무 가설 세움
-
통계적 가설 검정 과정을 통해 귀무가설 기각
-
안정적인 데이터라는 대립가설 채택
- 즉, 기무가설 기각이 되면 안정적인 시계열데이터지만 아니라면 그렇지 않다.
유의 확률 (p-값)
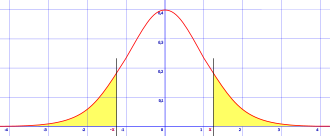
- 정의: 귀무 가설 맞다는 결과 < 실제 결과
--> 귀무가설의 가정이 틀렸다는 것을 방증
- 값이 <0.05 , p-value만큼 오류 가능성 하에 귀무가설 기각하고 대립가설 채택
Stasmodels 패키지와 adfuller메소드
- statsmodels 패키지
-
R에서 제공하는 통계검정, 시계열 분석 등의 기능을 파이썬에서도 이용하게 도움을 주는 통계 패키지
-
adfuller메소드: 주어진 timeseries에 대한 Augmented Dickey-Fuller Test 수행 코드
아이디어: Make Stationary
- 안정적인 특성을 갖도록 기존의 시계열 데이터 가공
-
1-1. 로그 함수 변환
- 추이에 따라 분산이 커지는데 p-value가 절반 이상 줄어들고 분산이 일정해진다.
-
1-2. Moving average 제거- 추세 상쇄하기
- 시간 추이에 따라 나타나는 평균값 변화 추세
- 추세제거: 거꾸로 Moving Average(rolling mean) -ts_log
-
1-3. 차분(Differencing) - 계절성(Seasonality) 상쇄하기
- Trend에 잡히진 않으나 시계열 데이터 안에 포함된 패턴이 파악되지 않은 주기적 변화.
- 예측에 방해가 되는 불안정요소
- Moving Average제거로 상쇄 안된다.
- 계절적, 주기적 패턴
- 시계열을 한 스텝 앞으로 시프트한 시계열을 원래 시계열에 빼준다.
- 현재 스탭 - 직전 스탭 : 이번 스텝에서 발생한 변화량 의미
- 시계열 분해 기술 적용
-
seasonal_decompose 메소드: 시계열 안에 존재하는 trend, seasonality를 직접 분리한다.
-
moving average제거, differencing등을 거치지 않아도 안정적인 시계열 만든다.
-
순서
- 로그 변환 단계(ts_log)
- Original 시계열, Trend 와 Seasonality 제거 후 나머지 residual (Decomposing)
- get a low p-value
ARIMA모델
ARIMA모델 정의
-
AR(Autoregressive) + I(Integrated) + MA(Moving Average)
-
시계열 데이터 예측 모델을 자동적으로 만든다.
- AR(자기회귀, Autoregressinve)
-
과거 값들에 대한 회귀를 통해 미래 값 예측
-
Yt가 이젠 p개의 데이터의 가중합으로 수렴
-
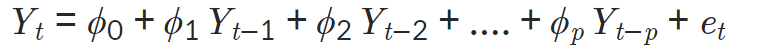
- AR은 시계열의 Residual에 해당부분 모델링한다.
- 가중치의 크기가 1보다 작은 가중합으로 수렴
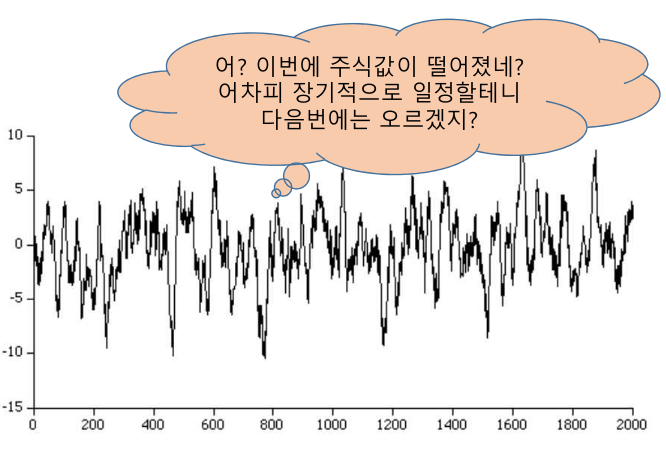
- 주식 시계열을 모델링한다.(균형 맞추기)
- MA(이동평균, Moving Average)

- MA는 Yt가 이전 q개의 예측오차값의 가중합으로 수렴
-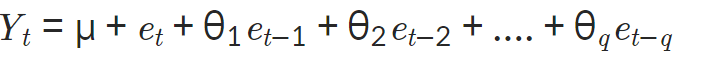
- MA는 시계열의 Trend에 해당 부분 모델
- 예측오차값 > 0, 관측값이 높으니 예측치 높이자
- 주식값이 증감패턴 지속 관점(추세적 증감)
- I(차분, Integration)
-
I는 Yt이 이전 데이터와 d차 차분의 누적 합
- I는 시계열의 Seasonality해당 부분 모델링
ARIMA 모델 p,q,d(모수)
-
모수: 핵심적인 숫자들을 정하기
-
p: 자기회귀 모형(AR)시차(BY PACF)
-
q: 이동평균 모형(MA)시차(BY ACF)
-
d: 차분누적(I)횟수
-
모수 선택법
-
ACF(Autocorrelation Function)
-
시차에 따른 관측치들 사이의 관련성 측정
-
주어진 시계열의 현재 값이 과거 값과 상관성 섦여
-
ACF plot에서 X축은 상관계수 나타내고 y축은 시차 수
-
-
PACF(Partial Autocorrelation Function)
-
다른 관측치의 영향력 배제한 후 두 시차의 관측치 간 관련성 측정
-
k이외의 모든 시차를 갖는 관측치의 영향력 배제 후 특정 두 관측치가 얼마나 관련 있는지 나타냄
-
-
