이진 탐색트리(BST)

이진 탐색 트리

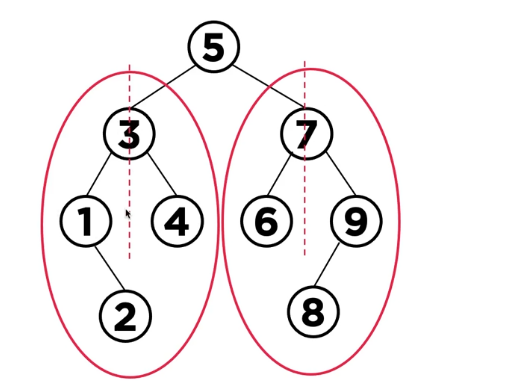
트리 구조 자체로는 데이터의 특성에 아무런 제약이 없다.

노드의 왼쪽 서브 트리에는 루트 노드보다 작은값이다.

노드의 오르쪽 서브 트리에는 루트 노드보다 큰 값이다.

중복된 값이 없다.

서브 트리는 다시 이진 탐색 트리가 되어서 위의 특징을 갖는다.

레벨에 생각 없이 트리의 가장 왼쪽 값이 최솟값이고 오른쪽 값이 최댓값입니다.

*삽입

중복된 데이터를 삽입할 경우 삽입이 되지 않습니다.

추가된 노드는 트리의 leaf에 삽입을 합니다.

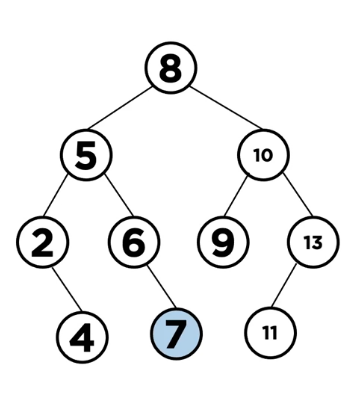
*삭제

• 삭제는 세 가지 경우가 있습니다. (삭제 데이터의 위치를 찾음)

  • 삭제할 데이터가 leaf:가장 아래 값을 숫자->null로 바꿔서 해결
  • 한 개의 자식 노드를 가질 경우: 삭제할 노드의 부모 와 자식 노드 사이에 넣기
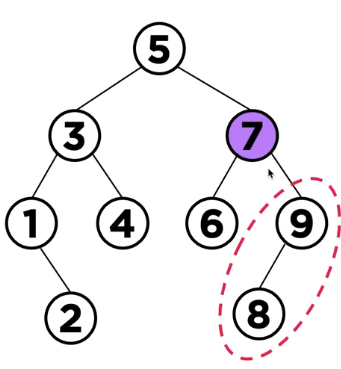
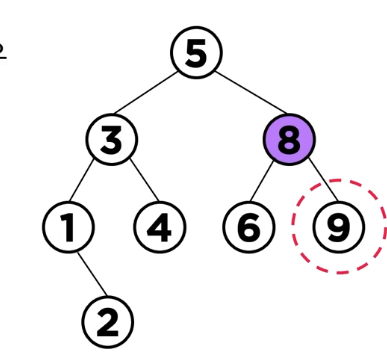
  • 두 개의 자식 노드를 가질 경우: 왼쪽 서브 트리의 최댓값과 교채하고 오르쪽 서브 트리의 최솟값과 교체

*삭제할 데이터가 leaf

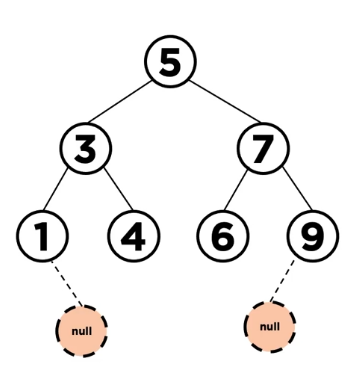
*한 개

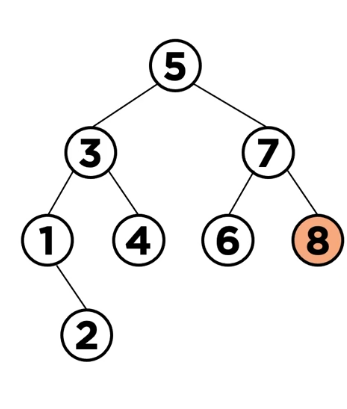
*두 개

code

class Node: #노드 클래스
    def __init__(self, val, left=None, right=None): #val인자 설정, left,  right 초기화
        self.val = val #value할당
        self.left = left #초기화된 left 할당
        self.right = right # 초기화도니 right할당
class BinarySearchTree: #이진탐색트리
    def __init__(self):
        self.root = None #루트 값 초기화
        self._size = 0 #각 레벨 별 숫자들 초기화 

    def insert_node(self, node, val): #노드 삽입 위치 함수: node와 value가 인자
        if node is None: #노드에 아무것도 없다면
            return Node(val) #val값을 출력
        if val < node.val: #value가 노드값보다 작다면
            node.left = self.insert_node(node.left, val) #왼쪽 노드에 삽입할 것
        elif val > node.val: # 크다면
            node.right = self.insert_node(node.right, val) #오른쪽 노드에 삽입할 것
        return node #최종 결과 반환

    def size(self): #사이즈 함수
        return self._size # 사이즈 반환

    def insert(self, val): #삽입 함수
        self.root = self.insert_node(self.root, val) #root에 노드 값 넣기
        self._size += 1 #사이즈 1 증가

    def contains(self, val): # val가 잘 들어갔나 학인 함수
        return self.contains_node(self.root, val) #노드 값이 잘 들어갔나 확인

    def contains_node(self, node, val): #node가 잘 들어갔나 확인하는 함수
        if node is None: #node가 비어있다면 
            return False #  잘 안 들어간 거니까 false반환
        if val == node.val: #값이 일치한다면
            return True #잘 들어간거니까 true
        if val < node.val: #값이 더 작ㄷ면
            return self. contains_node(node.left, val) #왼쪽 서브트리에 삽입
        return self.contains_node(node.right, val) # 오른쪽 서브 트리에 삽입

    def delete(self, val):#삭제할 위치 선정 함수
        return self.delete_node(self.root, val)#root값 삭제

    def delete_node(self, node, val): #노드 삭제 함수
        if node is None: #노드가 비어있다면
            return None #None출력
        
        if val < node.val: #val이 작다면
            node.left = self.delete_node(node.left, val) #왼쪽 삭제
        elif val > node.val: # 크다면
            node.right = self.delete_node(node.right, val)#오른쪽 삭제
        else:
            self._size -= 1 #삭제 했으니 사이즈 1 감소
            if node.left is None: #왼쪽 서브 트리 노드가 비어있다면
                return node.right #오른쪽 반환
            elif node.right is None: # 오른쪽 서브 트리 노드가 비어있다면
                return node.left #왼쪽 반환
            node.val = self.min_node(node.right) #오른쪽엔 최소
            node.right = self.delete_node(node.right, node.val) # 오른쪽 노드 삭제
        return node #노드값 리턴

    def min_node(node): #최소 노드
        min_val = node.val #최소 값과 노드 값 같다면
        while node.left is not None: #왼쪽 서브 노드는 비어있지 않다
            min_val = node.left.val #왼쪽 서브 노드 부분이 최솟값
            node = node.left #왼쪽 노드
        return min_val # 최솟값 부분 출력

    def preorder(self): #preorder
        ret = [] #빈 리스트 형성

        def visit(root): #방문하는 함수, 노드를 거쳐서 preorder만들기
            nonlocal ret #중첩함수 변수로 사용(아래 if)
            if root is None:  #root가 비어있다면
                return ret #ret반환
            ret.append(root.val) #root에 val삽입
            visit(root.left) #left방문하여 있나 확인
            visit(root.right)#right 방문하여 있나 확인
        visit(self.root)#잘 들어갔나 확인
        return ret #ret반환

    def inorder(self):# inorder만들기
        ret = [] #빈 리스트 형성

        def visit(root):#방문하는 함수, 노드를 거쳐서 inorder만들기
            nonlocal ret#중첩함수 변수로 사용(아래 if)
            if root is None:#root가 비어있다면
                return ret#ret반환
            visit(root.left)# #left방문하여 있나 확인
            ret.append(root.val)#root에 val삽입
            visit(root.right)#right 방문하여 있나 확인
        visit(self.root)#잘 들어갔나 확인
        return ret#ret반환

    def postorder(self):# postorder만들기
        ret = []#빈 리스트 형성

        def visit(root):#방문하는 함수, 노드를 거쳐서 postorder만들기
            if root is None:#root가 비어있다면
                return ret#ret반환
            visit(root.left)# #left방문하여 있나 확인
            visit(root.right)#right 방문하여 있나 확인
            ret.append(root.val)#root에 val삽입
        
        visit(self, root)#잘 들어갔나 확인
        return ret#ret반환
if __name__ == "__main__":
    btree = BinarySearchTree()
    for i in [3, 1, 2, 3, 8, 7]:
        print(f"btree.insert({i})")
        btree.insert(i)
        print(f"btree.size(): {btree.size()}")

    print("==================================")
    for i in [3, 1, 2, 3, 8, 7]:
        print(f"btree.contains({i}): {btree.contains(i)}")

    print("===================================")
    print(f"btree.preorder(): {btree.preorder()}")
    print(f"btree.inorder(): {btree.inorder()}")
    print(f"btree.postorder(): {btree.postorder()}")
    print("=====================================")

    print("btree.delete(2)")
    btree.delete(2)
    print("btree.delete(8)")
    btree.delete(8)
    print(f"btree.size(): {btree.size()}")

    print("==================================")
    for i in [3, 1, 2, 3, 8, 7]:
        print(f"btree.contains({i}): {btree.contains(i)}")

    print("===================================")
    print(f"btree.preorder(): {btree.preorder()}")
    print(f"btree.inorder(): {btree.inorder()}")
    print(f"btree.postorder(): {btree.postorder()}")
    print("=====================================")