힙(Heap)

힙(Heap)

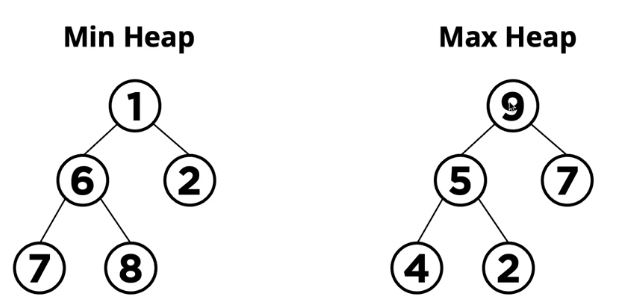
완전 이진 트리

최대 힙: 부모 노드의 값은 항상 자식 노드보다 크거나 같기에 루트 노드는 트리의 최댓값입니다.

최소 힙: 부모 노드의 값은 항상 자식 노드보다 작거나 같기에 루트 노드는 트리의 최솟값입니다.

최대/최소를 기준으로 데이터를 찾는 연산을 빠르게 할 수 있다 O(1)

삽입: O(logN)

삭제 O(logN)

활용

우선순위 큐

데이터가 들어온 순서에 상관없이 우선순위가 높은 데이터 순으로 처리가 되기에 OS의 작업 스케줄링할 때 사용이 됩니다.

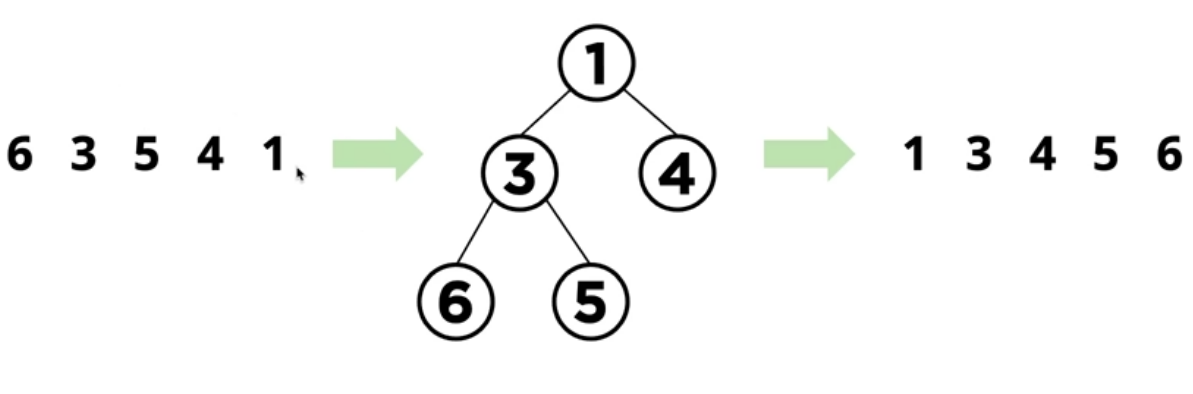
힙 정렬

힙 자료구조의 특성을 이용한 정렬 방법

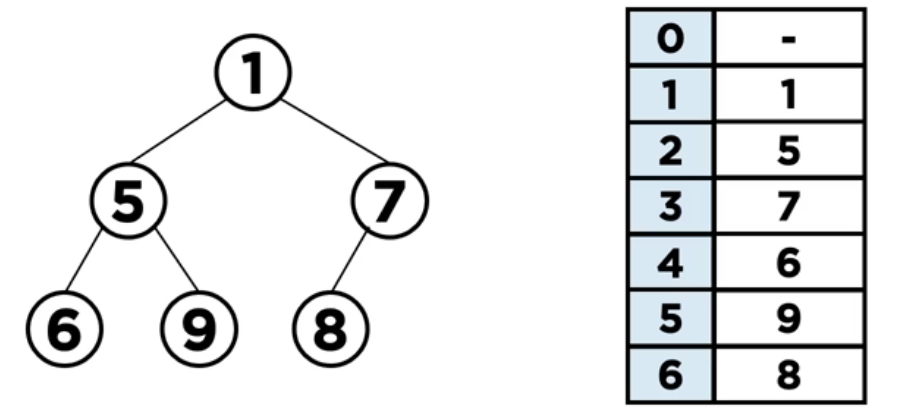
배열로 표현하기

완전 이진 트리이기 때문에 빈 값이 없는 일차원 배열로 표현이 가능

Heapify

힙의 재구조화로 데이터 추가/삭제 후에도 힙의 속성을 유지합니다.

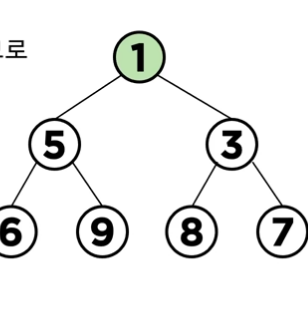
i) 데이터 1삽입(최솟값)

• 완전 이진 트리의 형태를 유지해야하므로 우선 leaf노드에 삽입

• 힙의 조건을 만족하는지 확인

• 삽입된 노드와 부모 노드의 값을 바뀜

ii) 데이터 9삭제 (최댓값)

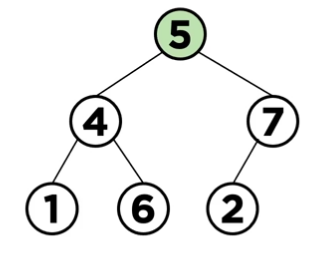
• 마지막 노드를 루트 노드로 가져온다

• 힙의 조건을 만족하는지 확인

• 자식 노드와 위치를 바꿈

code

class MaxHeap: #최대 힙
    def __init__(self): #시작은 국룰
        self.data = [] #빈 리스트 만들어서 숫자 넣기
    
    def size(self): #사이즈 함수
        return len(self.data) #길이 반환

    def insert(self, value): #삽입함수
        self.data.append(value) #빈 리스트인 data에 값 넣기
        self.heapify(len(self.data) -1) #전체 - 1

    def pop(self): #빼는 함수
        ret = self.data[0] #data의 첫 부분
        self.data[0] = self.data[-1] #같다
        self.data.pop() #데이터빼기
        self.max_heapify() #최대힙 구하기
        return ret #변화된 값 확인

    def peek(self): # 읽기만하는 함수
        return  self.data[0] #확인작업

    def max_heapify(self, index): #최대 힙
        left = 2 * index + 1 #왼쪽부분 2개 건너뛰고 한 칸 더
        right = 2 * index + 2 #오른쪽부분 2개 건너뛰고 두 칸 더
        largest = index #최대

        if left < len(self.data) and self.data[left] > self.data[largest]:
            largest = left
        if right < len(self.data) and self.data[right] > self.data[largest]:
            largest = right
        if largest != index:
            self.data[index], self.data[largest] = self.data[largest], self.data[index]
            self.max_heapify(largest)

    def heapify(self, index):
        parent = (index - 1) // 2
        if parent >= 0:
            if self.data[index] > self.data[parent]:
                self.data[index], self.data[parent] = (
                    self.data[parent],
                    self.data[index],
                )
                self.heapify(parent)
if __name__ == "__main__":
    max_heap = MaxHeap()
    for i in range(5):
        print(f"max_heap.insert({i})")
        max_heap.insert(i)
        print(f"max_heap.peek(): {max_heap.peek()}")

    print("===========================================")
    for _ in range(5):
        print(f"max_heap.size(): {max_heap.size()}")
        print(f"max_heap.pop(): {max_heap.pop()}")
max_heap.insert(0)
max_heap.peek(): 0
max_heap.insert(1)
max_heap.peek(): 1
max_heap.insert(2)
max_heap.peek(): 2
max_heap.insert(3)
max_heap.peek(): 3
max_heap.insert(4)
max_heap.peek(): 4
===========================================
max_heap.size(): 5
max_heap.pop(): 4
max_heap.size(): 4
max_heap.pop(): 3
max_heap.size(): 3
max_heap.pop(): 2
max_heap.size(): 2
max_heap.pop(): 1
max_heap.size(): 1
max_heap.pop(): 0