Information Content
- 정의: 어떻게 정보를 정량적으로 표현하는가
-
조건:
- 일어날 가능성이 높은 사건은 정보량이 낮다
- 반드시 일어날 사건에는 정보가 없는 것과 마찬가지이다
- 일어날 가능성이 낮은 사건은 정보량이 높다
- 두 개의 독립적인 사건, 전체 정보량은 각각의 정보량을 더한 것과 같다(log성질)
-
정보량(information content)
*P(x):사건 x가 일어날 확률
-
공식
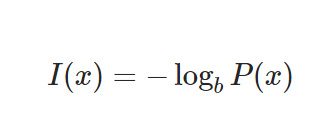
-
그래프
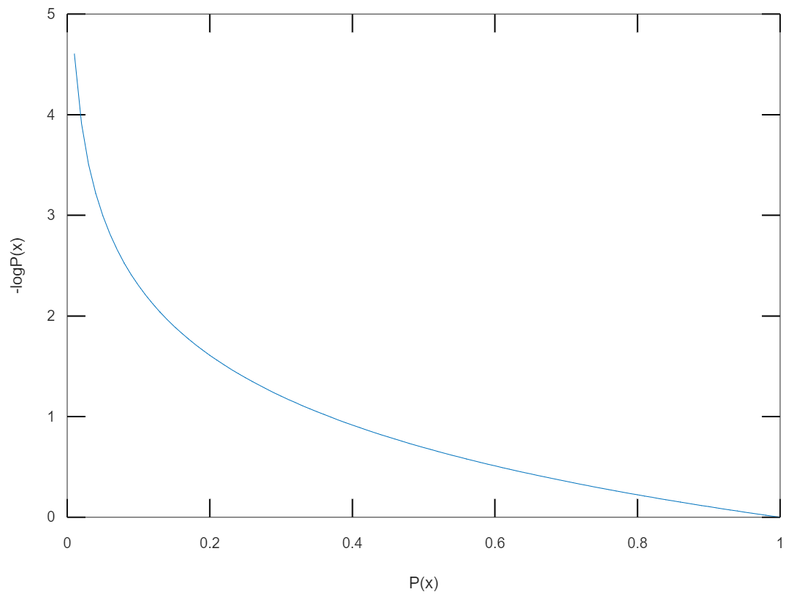
- Code 구현
import numpy as np
import math
import random
# 주머니 속에 들어있는 공의 개수입니다. 숫자를 바꾸면서 실험해보세요!
total = 1000
#---------------#
count = 1 # 실험이 끝날 때까지 꺼낸 공의 개수
# 1부터 total까지의 정수 중에서 하나를 뽑고 total과 같으면 실험 종료
# total=1000인 경우 1~999: blue / 1000: red
while True:
sample = random.randrange(1,total+1)
if sample == total:
break
count += 1
print('number of blue samples: '+str(count-1))
print('information content: '+str(-math.log(1/count)))Entropy
-
정의: 특정 확률 분포를 따르는 사건들의 평균
-
특징: 각 경우의 수가 가지는 정보량에 확률을 곱한 후 더한 것.
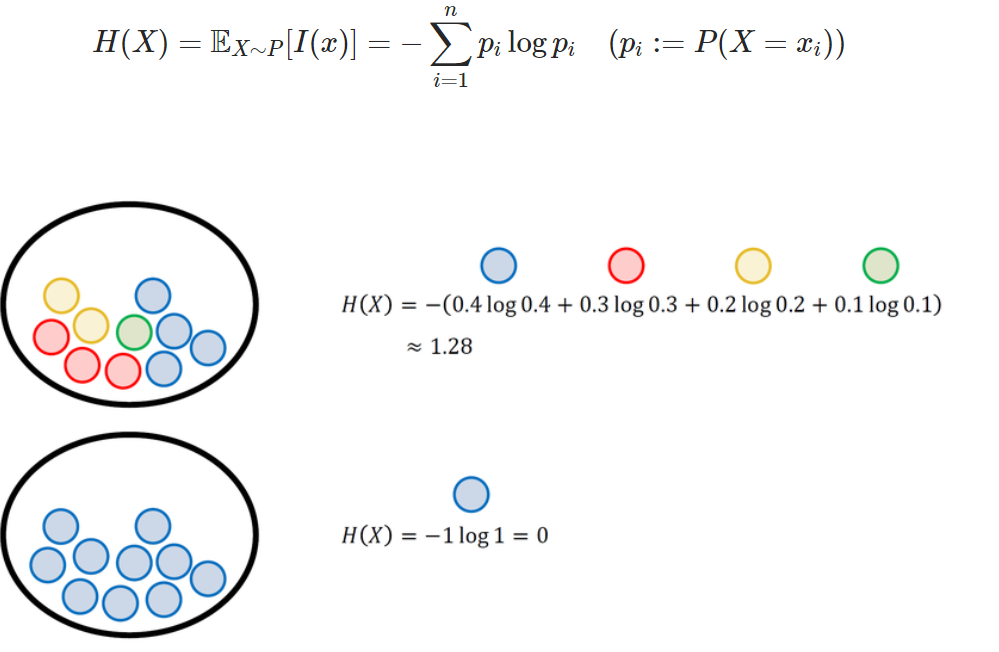
For Discrete Random Variables
-
이산 확률 변수이다.
-
여러 가지 경우가 많을 때는 엔트로피가 높다
-
같은 경우의 수들이 많을 때는 엔트로피가 낮다
-
정확히 규정할 수 없고 경우에 따른 변수들이 많다.
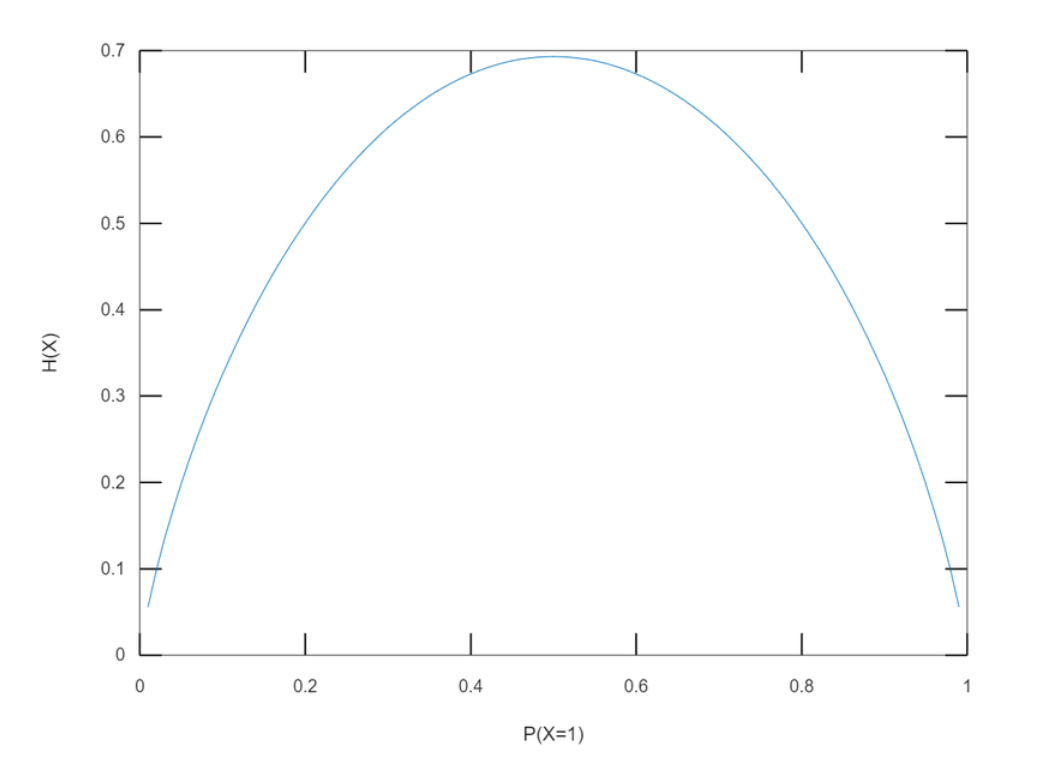
균등 분포
- 정의: 확률 변수가 가질 수 있는 값의 경우들이 같을 때, 사건의 확률들이 비슷할 수록 엔트로피값은 증가한다.
For Continuous Random Variables
-
연속확률 변수엔트로피(미분 엔트로피)이다
-
유한합이 아니라 적분의 형태로 정의한다.
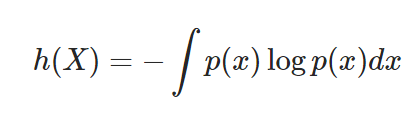
Kullback Leibler Divergence
- 필요성
: 머신러닝에서는 생성모델이 데이터와 모델을 가지고 표현하는 여러 확률 분포와 베이지 이론을 사용하여 데이터의 실제 분포를 간접적으로 모델링하므로 두 확률 분포의 차이를 줄여야하여 DKL(P||Q)를 최소화하는 방향으로 모델 학습.
- 정의
: 두 확률 분포의 차이를 나타내는 지표
- 식
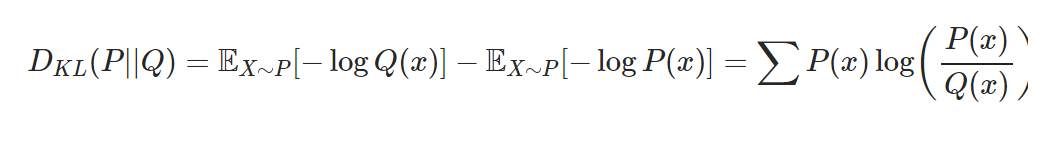
-
P(x): 데이터가 따르는 실제 확률 분포
-
Q(x): 모델이 나타내는 확률 분포(근사적인 분포) -> 발생하는 엔트로피의 변화량 나타냄
-
두 확률 분포의 KL
-
P(x)를 기준으로 계산된 Q(x)의 평균 정보량
-
P(x)를 기준으로 계산된 P(x)의 평균 정보량
-
위의 두 경우의 차이를 정의한다(거리 함수와 비슷한 성질을 가짐)
-
기준되는 확률분포가 존재하기에 DKL(P∣∣Q) 와 DKL(Q∣∣P)의 값이 같지 않ㅇ므
-
대표적인 특성
-
DKL(P||Q)>= 0
-
DKL(P||Q) = 0 if and only if P = 0
-
non-symmetric:
DKL(P||Q) != DKL(Q||P)
-
Cross Entropy
- 정의: P(x)를 기준으로 계산한 Q(x)의 엔트로피.
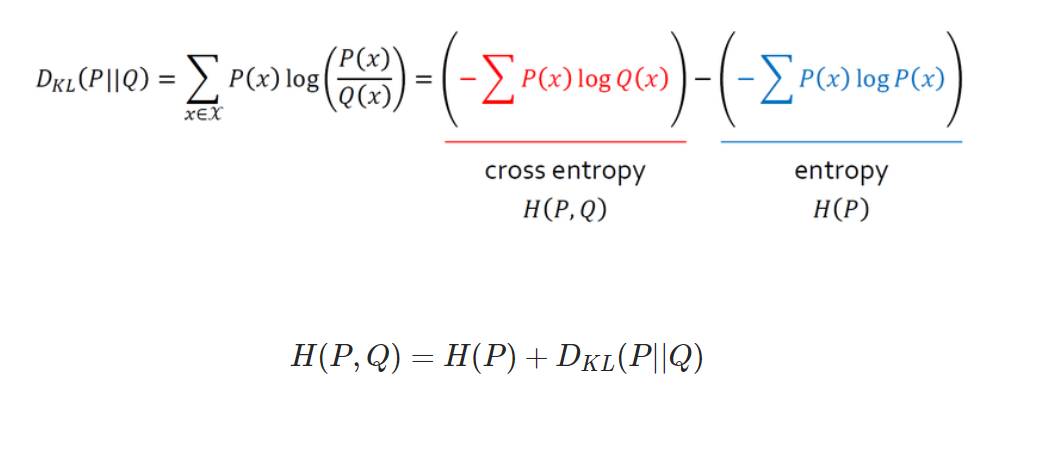
-
P(x)는 데이터의 실제 분포이기에 바꿀 수 없는 고정값입니다.(파란색 부분)
-
Q(x)는 우리가 바꿀 수 있고 KL를 최소화하는 것은 곧 빨간색 부분으 최소화 하는 것과 같다.
-
특징
- 정답셋의 확률분포 P와 우리 모델의 추론 결과의 확률분포 Q의 차이 KL을 최소화하는 것은 교차엔트로피를 최소화는 것과 같다.
Cross Entropy Loss
-
loss 함수(손실 함수): 확률 분포와 데이터가 따르는 실제 확률 분포 사이의 차이를 나타내는 함수
-
모델의 확률 분포는 파라미터에따라 달라진다.
-
분류문제:
- 로지스틱함수로 출력결과가 표현됨.
- 데이터의 라벨은 one-hot encoding로 표현
-
softmax함수: 분류 클래스가 2개인 로지스틱 함수를 n개 일때로 확장시킬 때 이용.
-
softmax함수와 데이터의 확률분포 차이가 분류문제의 손실함수가 된다.
-
즉, KL 최소화 = cross entropy
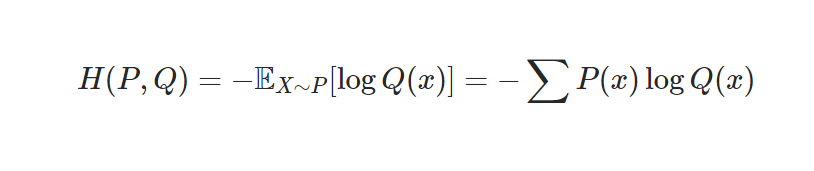
-
처리 과정
i) 입력데이터의 특성 값
ii) 모델 통과(one-hot encoding)
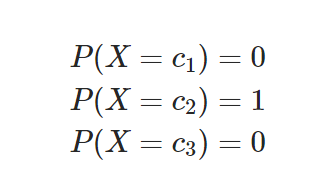
iii) 출력 레이어의 소프트맥스 함수 이용
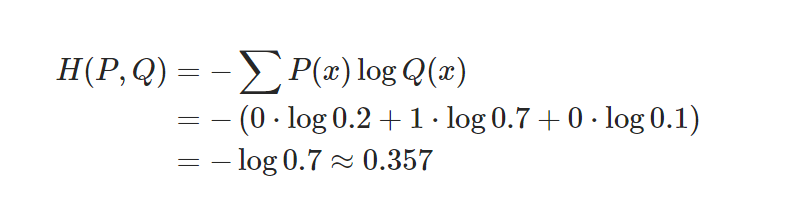
iv) 각각의 클래스에 속할 확률이 계산(모델이 추정한 확률 Q(x) 구성 값)
-
Code
import numpy as np
import random
# generate random output
#-----------------#
# can be modified
class_num = 4
#-----------------#
q_vector = []
total = 1
for i in range(class_num-1):
q = random.uniform(0,total)
q_vector.append(round(q,3))
total = total - q
q_vector.append(total)
softmax_output = np.array(q_vector)
print(softmax_output) # Q(x)가 랜덤값으로 생성되는 것이 아닌 모델의 예측을 통해 얻음#-----------------#
# can be modified
class_index = 1
#-----------------#
#P(x)를 생성해 Cross Entropy 계산
p_vector = np.zeros(class_num) # P(x)는 one-hot vector
p_vector[class_index-1] = 1
cross_entropy = -np.sum(np.multiply(p_vector, np.log(softmax_output)))
print('model prediction: '+str(softmax_output))
print('data label: '+str(p_vector))
print('cross entropy: '+str(round(cross_entropy,4)))Cross Entropy와 Likelihood의 관계
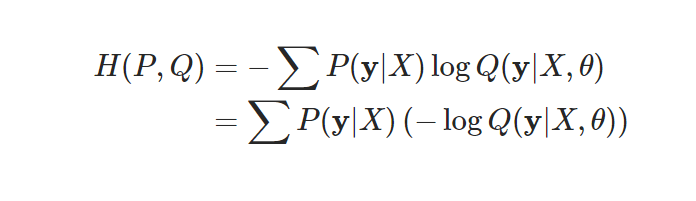
- Cross entropy를 최소화하는 파라미터 값을 구하는 것은 negative log likelihood를 최소화하는 파라미터 구하기
Decision Tree와 Entropy
- 특징:
- 엔트로피 기준으로 정보 이득은 얻을 수 있지만 분류 기준을 크게 세우진 않는다 왜냐하면 모델 정확도 향상에 낫다는 것을 알 수 있기 때문이다. 무슨 말이냐면, Decision Tree 같은 경우 분류 기준은 임의로 정한 것이기에 무한정으로 쪼개서 엔트로피는 떨어뜨릴 수 있으나 Overfitting의 결과를 만들 수 있기 때문이다.
- 갖고 있는 데이터에서 어떤 기준으로 전체를 나눴을 때 나누기 전보다 엔트로피가 감소여부를 따져서 그 만큼 모델 내부에 정보이득을 얻었다고 본다.

-
S: 전체 사건의 집합
-
F: 분류 기준으로 고려되는 속성 집합
-
f ∈ F: f는 F에 속하는 속성
-
Sf: f속성을 가진 S의 부분집합
-
|X|: 집합 X의 크기(원소의 개수)
-
e(X): X라는 사건 집합이 지닌 엔트로피
-
IG(S,F): F라는 분류 기준을 선택할 때의 엔트로피를 전체 사건의 엔트로피에 빼준 값으로 분류기준 채택을 통해 얻는 정보 이득의 양
-
계산방법:
i) F에 대한 정보 이득 계산
ii) 가장 정보 이득이 큰 순서대로 전체 사건 2등분
iii) i) 와 ii)를 사건마다 반복
iv) 세부 분류 기준 계속 찾기
v) 위의 과정들이 트리와 비슷해서 의사결정나무(Decision Tree)로 불림
vi) Code 구현
