베이지안 머신러닝 모델

머신러닝 목표

• 모델 형성 후 파라미터의 갓 조절을 통해 데이터 분포를 간접적으로 표현

• 모델 표현하는 확률 분포를 데이터의 실제 분포에 가깝게 만드는 최적 파라미터 값 찾기

베이지안 머신러닝

• 데이터를 통해 파라미터 공간의 확률 분포 학습

• 모델 파라미터가 고정된 값이 아닌 불확실성을 가진 확률 변수로 본다

• 데이터 관찰하면서 업데이트 값 본다.

확률 변수의 모델 파라미터

• R^2 공간 안의 모든 점(a,b)가 일차함수 y=ax+b를 유일하게 결정하여, 저 공간 안의 모든 점들은 일차함수들로 이루어진 함수 공간의 서로 다른 원소에 각각 대응.

• 파라미터 공간

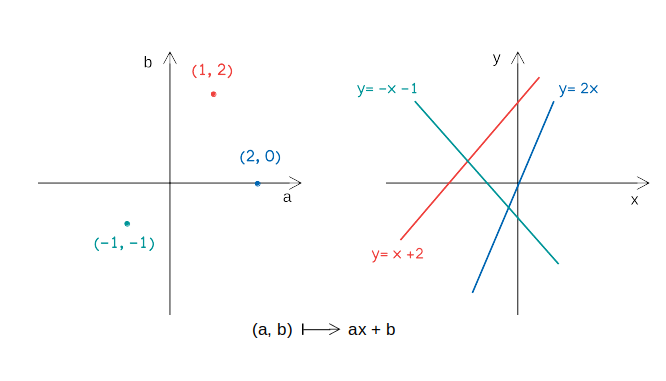
• R^2공간에 원소(a,b)가 있는 것으로 파라미터 공간에 주어진 확률 분포로 생각 가능

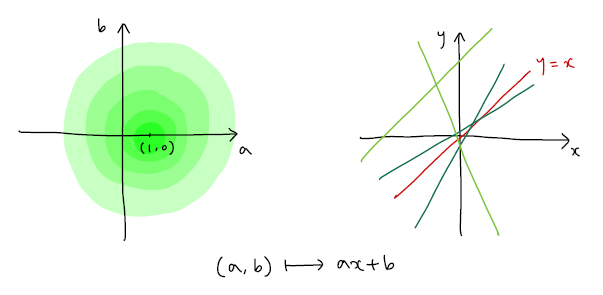
- 평균이 (1,0)인 정규분포

- a와 b의 값이 1과 0에 가깝다

Posterior , Prior, Likelihood 사이 관계

0. 데이터 집합 X가 주어졌을 때, 데이터를 따르는 확률분포 p(X)를 가장 잘 나타내는 일차함수 모델 찾기

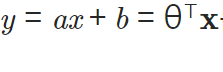
1. Prior(사전 확률)

• 정의: 데이터 관찰 전 공간에 주어진 확률 분포 p(θ)로 정규분포 혹은 특성분포이다

2. Likelihood(가능도, 우도)

• 정의: prior 분포를 고정시켜, 주어진 파라미터 분포를 통해 데이터가 상태가 좋은 지 계산한 값

• 식: 파라미터의 분포가 정해졌을 때 x라는 데이터 관찰될 확률

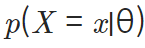
• 특징:

  	- θ에 의해 결정되는 함수라서 가능도 함수를 L(θ∣x)라고도 표현
  
  	- likelihood가 높다는 것은 파라미터 조건에 지정한 데이터가 관측될 확률 높음

  • 최대가능도 추정(MLE): likelihood값을 최대화하는 방향으로 모델 학습 방법
  • likelihood값이 작다는 의미: 모델 예측값과 데이터라벨의 차이가 크다입니다
  • likelihood값으 크다는 의미: 모델 예측값과 데이터 라벨의차이가 작다.(우리가 찾아야하는 거)

3. Posterior(사후 확률)

• 정의: 데이터 관찰한 후 계산되는 확률

• 특징: 직접 계산하여 최적의 θ값을 찾는 것이 아닌, prior와 likelihood에 관해 식 변형 후 그 식을 최대화하는 파라미터 θ 찾기

• 최대 사후 확률 추정(MAP): posteriro를 최대화 하는 방향으로 모델 학습

4. posterior와 prior, likelihood사이의 관계

• 확률 곱셈 정리

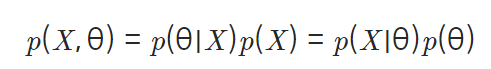
• 베이즈 정리

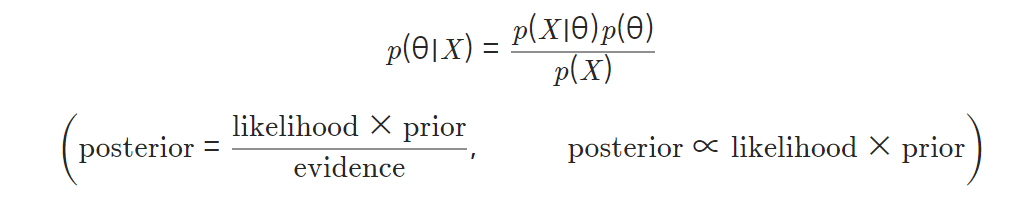
• 설명

  	- 정확한 확률 분포 알 수 없어서 posteriror의 값을 직접 구함 X

  • p(X)로 나누는 부분이있기에 계산 못함
  • p(X)는 고정된 값이고 likelihood와 prior 계산 가능
  • 우변을 최대화하는 파라미터값 구하기 가능

Likelihood와 머신러닝

링크텍스트

0.Preview

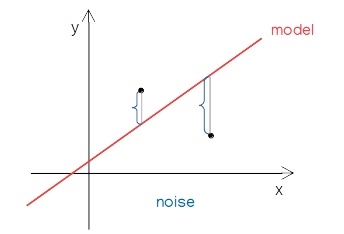
• 한정된 파라미터로 실제 분포 근사

• 100% 정확도는 불가

• 입력 데이터~> 예측한 출력 데이터 와 실제값 사이의 오차 발생

• 원인: 데이터에 이미 노이즈가 있기 때문이다.

1. 하나의 likelihood p(yn∣θ,xn)을 통해 출력값 분포 에측

• 모델 : 선형 모델 y=θ^⊤ * x

• 출력값의 분포: 모델의 예측값에 노이즈 분포 더함

• 노이즈 분포(정규분포)

  	- 평균: 0

  • 표준편차: σ

  • 출력값 분포:

    - 평균: θ^⊤ * xn
    
    - 표준편차:  σ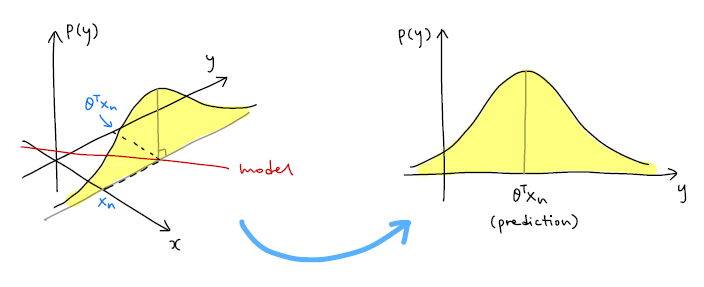

    

    - p(y)추가: 출력값 분포 나타냄

MLE

0. 잠깐 맛보기를 했던 것을 여기서 집중적으로 다뤄보겠습니다.

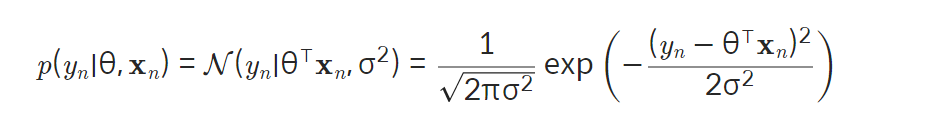
• 모델 파라미터 : θ

• 데이터 포인트(xn, yn)

• 좋은 모델은 모든 데이터 포인트의 likelihood 값 크게 만드는 모델.

-> HOW?

: 데이터 포인트가 서로 독립이고 같은 확률 분포 따름(i.i.d)

: likelihood p(Y∣θ,X)는 데이터 포인트 각각의 likelihood를 모두 곱한 값

• likelihood 대신 log likelihood를 최대화하는 파라미터 구함

  	- 로그의 성질이용( 곱셈 연산이 덧셈으로 바뀌어 미분 계산 편리)
  
  	- likelihood값이 0에 가까워지고 이 수들 곱하면 CPU연산이 불가하여 언더플로우 발생하는 문제를 해결해줌
  
  
  	-  로그함수는 단조증가이므로 likelihood를 최대화하는 파라미터와 log likelihood를 최대화하는 파라미터 값이 같아서 학습 결과에 영향을 주지 않음
  
  	- 로그 계산식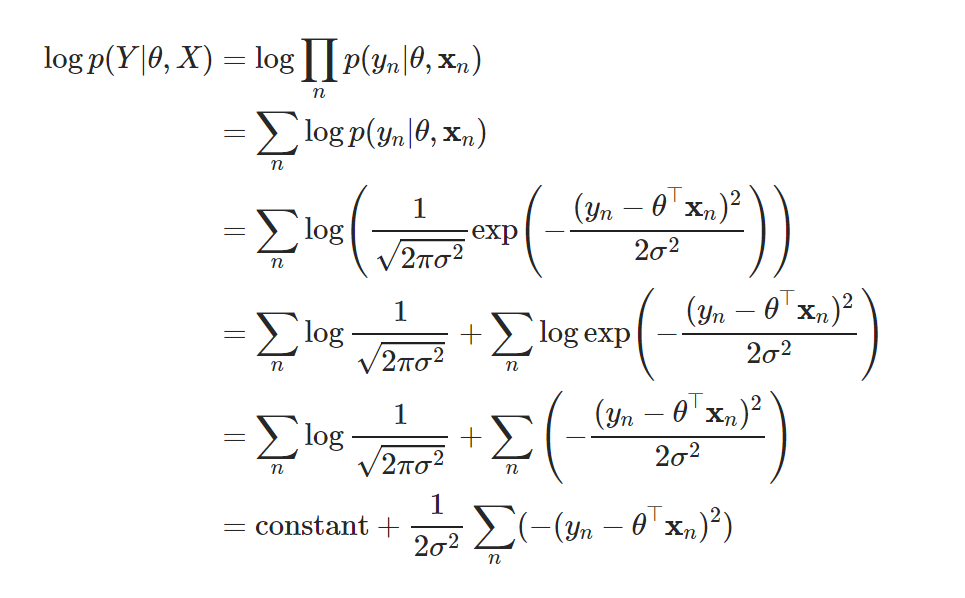

  
  

• 최대화

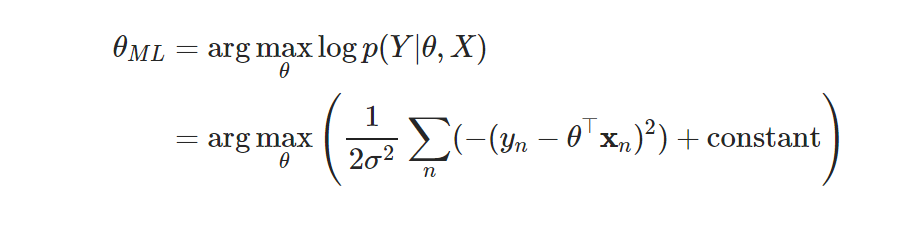
• 손실함수 최소화

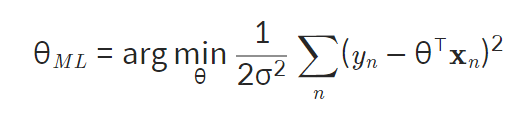
• 최소 제곱법

• 최적 파라미터

• 유도 과정
  

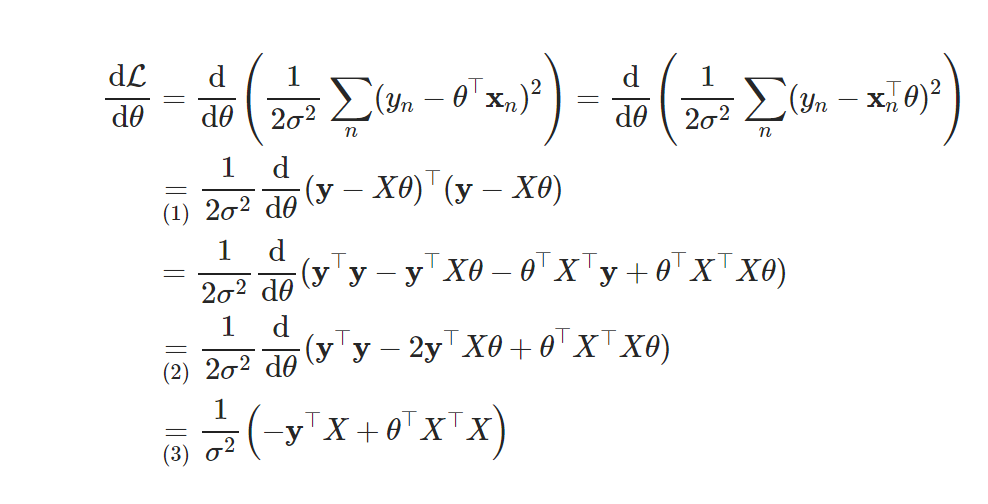
MLE 최적해 구하기

• Code 구현

링크텍스트

MAP

• ML모델의 최적 파라미터 찾는 방법

• p(θ∣X)에서 확률 값을 최대화하는 파라미터 θ찾기

prior분포의 등장

• 배경: 선형 회귀 문제에서 MLE의 의존도가 심함(장점은 있지만, 노이즈가 많을 시 이상치 데이터가 있어서 모델의 안정성을 떨어뜨림)

• 특징:

  	- 관찰된 데이터가 없을 때 파라미터 공간에 주어진 확률 분포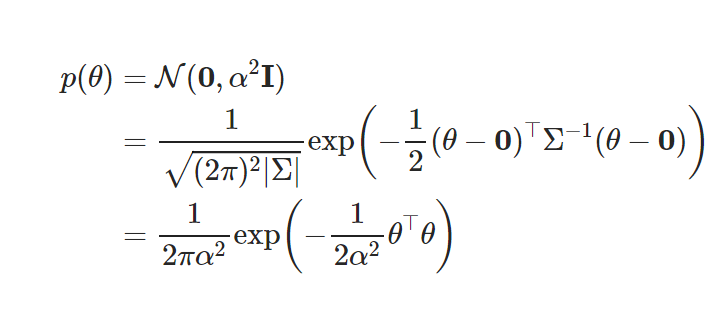

  

  • negative log posteriror 최소화하는 파라미터 구하기

    

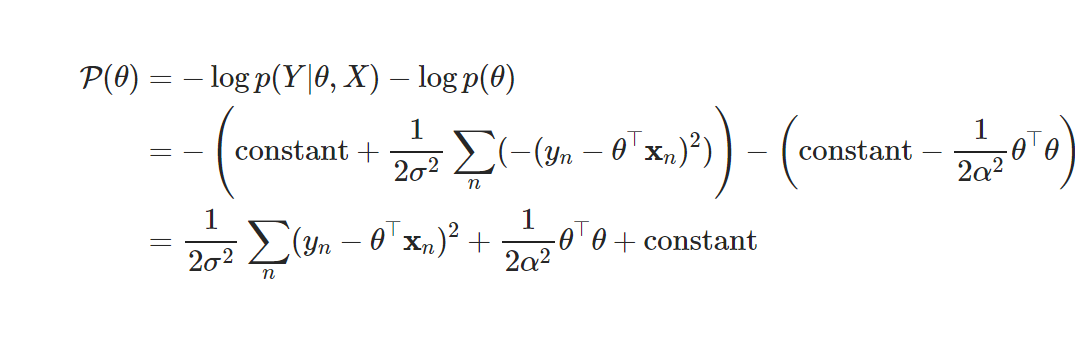
    		- 미분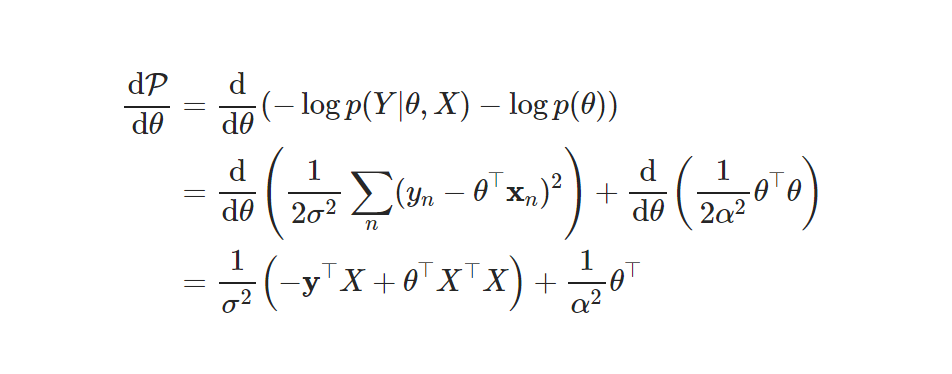

    

  • MAP 최적 파라미터

    

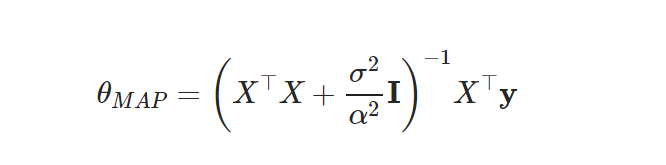
    • I항이 더해짐(MLE와 다른 점)

MAP as L2 regularization(최소 제곱법의 정규화)

• 식

• 손실 함수에 파라미터의 크기에 관한 식 더함

  -> 오버피팅 예방

• 평균(0,0)인 정규분포!

• 0에 가깝게 학습

MAP 코드

링크텍스트