CEVAE / Causal Effect Inference with Deep Latent-Variable Models

"Causal Effect Inference with Deep Latent-Variable Models"은 2017년 NIPS (Neural Information Processing Systems) 컨퍼런스에서 발표된 논문입니다. 이 논문은 딥러닝과 잠재 변수 모델을 사용하여 인과 효과(Causal Effect)를 추론하는 방법을 다루고 있습니다.

Abstract

• 관찰 데이터에서 인과 효과(causal effects)를 추론하는 가장 중요한 측면은 원인과 결과 모두에 영향을 미치는 혼동변수(confounders)를 처리하는 것

  • 혼동변수란 원인(약물 투여 등)과 그 결과 모두에 영향을 미치는 요소들, 잠재적 교란변수
  • 예를 들어, 특정 치료가 환자에게 어떤 영향을 미치는지를 파악하는 것이 포함

• 연구는 confounders를 요약하는 알려지지 않은 잠재 공간과 causal effects를 동시에 추정하는 방법을 제안

  이 방법은 인과 구조와 proxies(대리자)를 사용한 추론의 인과 구조를 따르는 Variational Autoencoders (VAE)에 기반
  

Introduction

목표 : 의료 및 교육과 같은 분야에서 관찰 데이터에서 개인 수준의 인과관계 효과를 학습

예를 들어 약물이 환자의 건강에 미치는 영향을 이해하거나 교육 방법이 학생의 졸업 가능성에 미치는 영향을 이해하기 위한 경우, 개인에 대한 원인의 인과효과를 이해하는 것은 근본적인 문제임

요점 : 관찰할 수 있는 데이터로부터 인과 관계를 추론하는 데 있어 원인과 결과에 모두 영향을 미치는 confounder를 찾는 것이 중요함

• counfounder를 측정할 수 있는 경우 counfounder의 효과를 고려하는 방법으로 covariate adjustment 또는 propensity score re-weighting를 통해 제어하는 것이 있음 *covariate adjustment : 다중 회귀 분석을 이용하여 인과 관계에 영향을 미치는 혼동변수를 제거하는 방법 *propensity score re-weighting : 원인을 받을 가능성에 따라 가중치를 계산하여 조절하는 방법
  
• counfounder가 숨겨져 있거나 측정되지 않은 경우 (일반적인 경우라고 할 수 있음) 원인의 결과에 대한 효과를 추정하는 것은 불가능 예를 들어, 사회경제적 지위는 환자가 이용 가능한 약물과 환자의 일반적인 건강 모니터링에 모두 영향을 미칠 수 있음 ⇒ 사회경제적 지위는 약물과 건강 결과 간의 혼동 변수로 작용
  

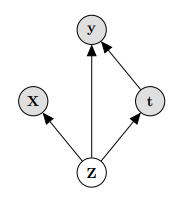
X : observed (noisy) confounder
Z : hidden confounder
t : treatment(intervention)
y : outcome

문제점 : 현실 세계에서 모든 혼동 변수를 찾기는 어려움

⇒ 연구에서는 surrogate-rich 환경에 맞는 인과 효과 추론의 대안적 접근 방법을 제안

*surrogate-rich setting이란 대체 변수가 풍부하게 존재하는 상황 (ex.사회경제적 지위를 직접 측정하는 것이 어렵기 때문에 우편 변호나 직업 유형 같은 근사치 사용)

숨겨진 혼동 변수를 발견하는 동시에 원인과 결과에 어떻게 영향을 미치는지 추정하는 잠재변수 모델링, 특히 (approximate) maximum-likelihood 방법에 중점

많은 경우 latent-variable model이 계산적으로 다루기 힘들지만, 지난 몇 년 동안 잠재 변수 모델링을 위해 계산적으로 효율적인 알고리즘이 많이 개발되는 등 진전이 있었음

저자는 그중 VAE가 images, volumes, time-series, fairness 등의 다양한 어려운 문제를 해결하는데 매우 효과적임이 입증되었으며, 데이터 생성 과정과 latent variable에 대해 덜 엄격한 가정을 할 수 있다는 장점이 있으나 아직 이론적 근거는 아직 부족하다고 말함

연구에서 제안한 방법은 noisy proxies가 존재할 때 숨겨진 confounder에 대해 더 견고하다는 것을 입증 (그러나 selection bias 문제는 future work로 남겨둠)

Hypothesis

• 인과관계를 식별하기 위해 그림의 인과모델을 가정
• z와 x의 joint distribution이 관측값에서만 대략적으로 복구될 수 있다고 가정
  • 위 가정은 숨겨진 confounder가 관측된 변수과 관련이 없는 경우 불가능하지만, 이것이 가능한 경우가 많음

Confounder

아래 식이 성립하면(같지 않으면) confounder가 존재

t를 조작했을 때 y가 받는 영향이 조건부확률과 같으면(독립) t가 원인이나, 다르면 confounder가 존재한다는 것을 의미

그러나 몇 가지 confounder를 관측하는 것은 가능 ⇒ 제안하는 방법에서는 proxies를 이용해서 숨겨져있는 latent space를 찾음

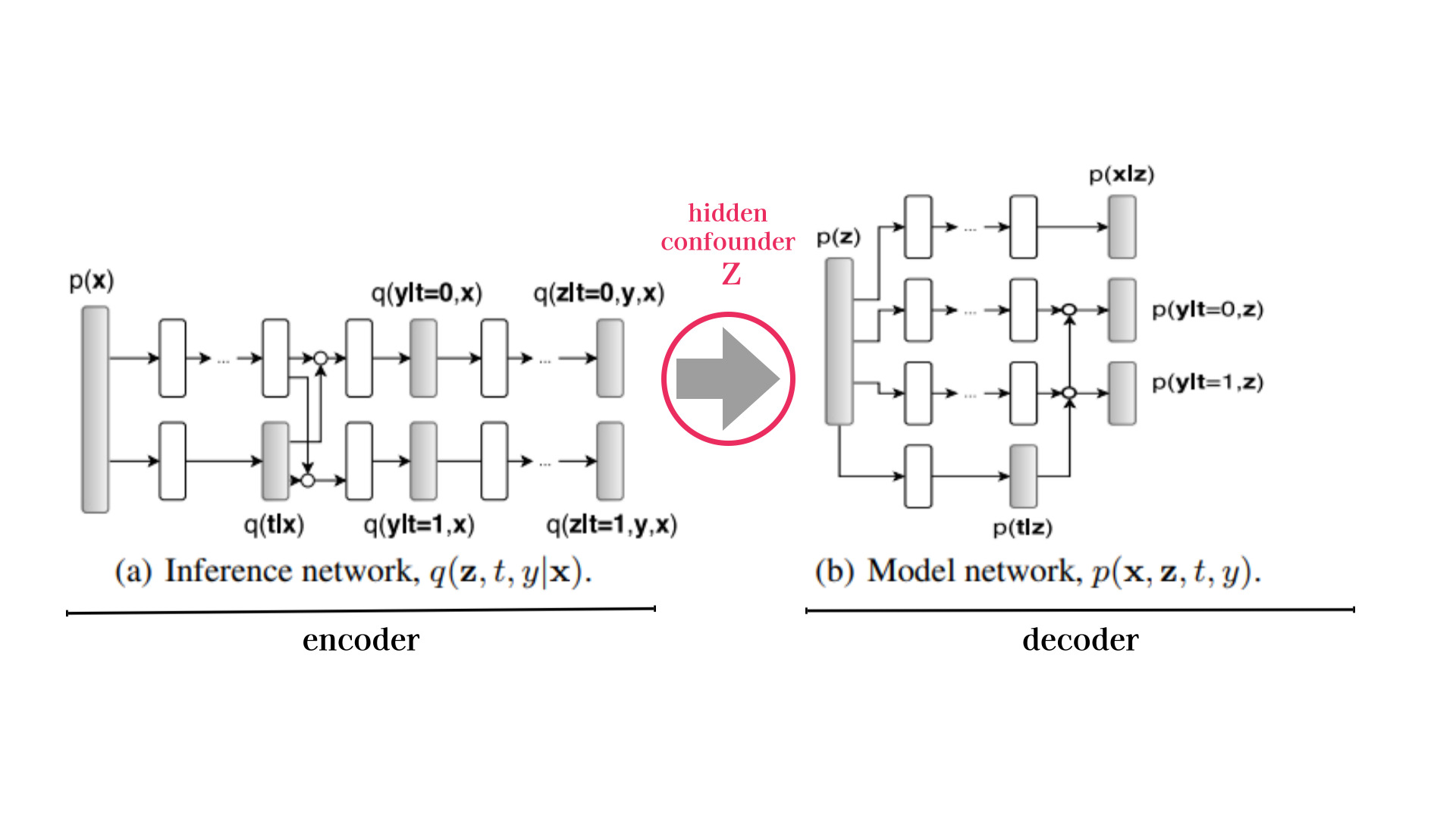
Overall architecture of the Causal Effect Variational Autoencoder(CEVAE)

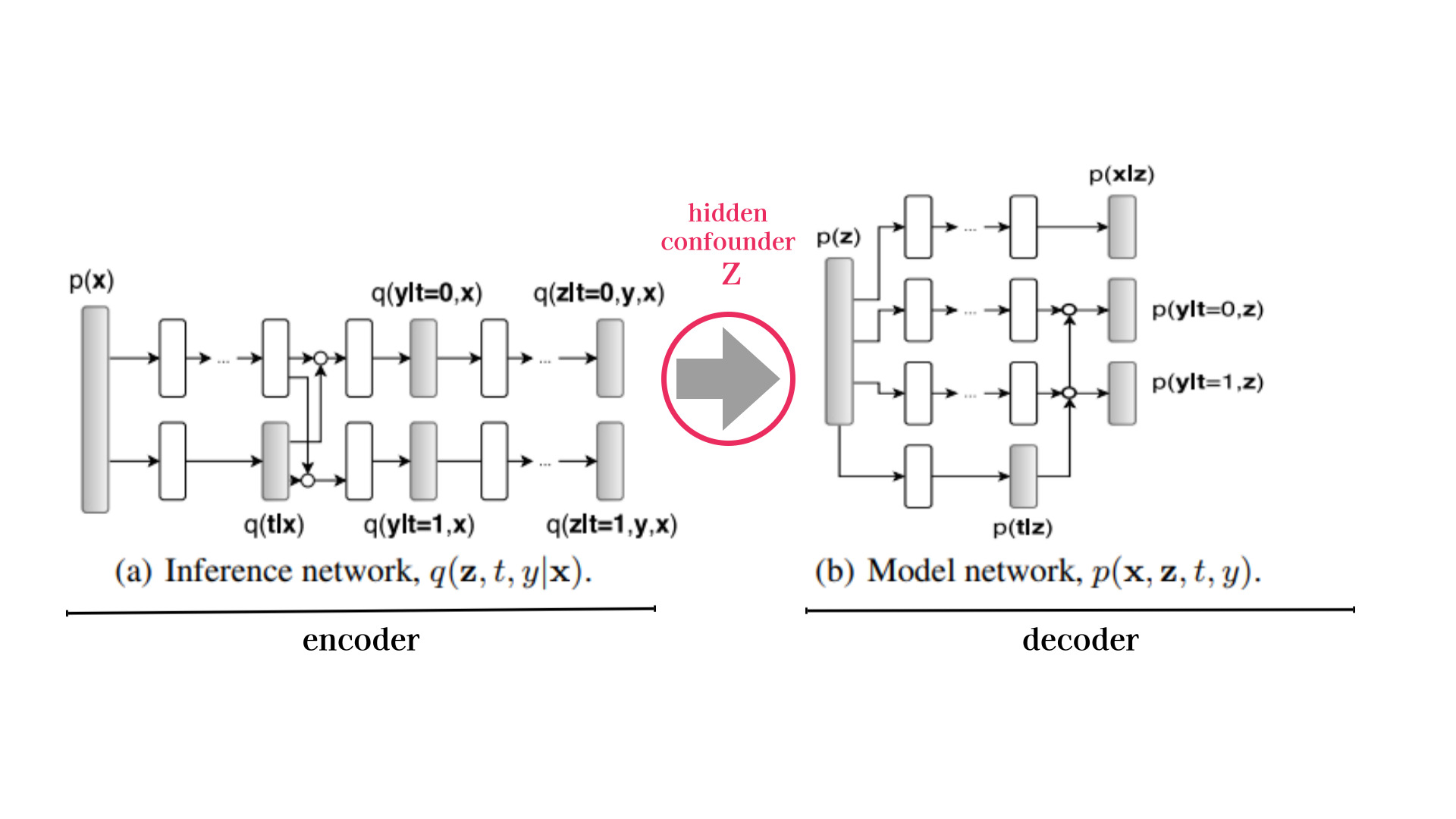confounder q(z|t, x, y)를 모델링

Objective Function

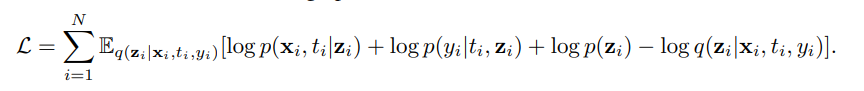
양변을 p(z)로 나눠주면 결국 VAE의 lower bound가 됨

첫번째 term은 reconstruction이 되고 두번째 term은 regularization이 됨(앞 term은 높이고, 뒤 term은 높여야 함)

Experiments

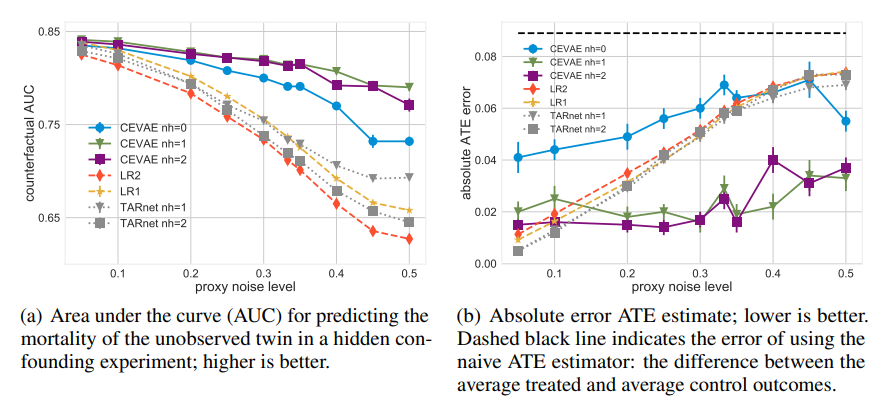
causal inference methods를 평가하는 것은 항상 어렵지만 여기서는 두가지 벤치마크 데이터셋에서 좋은 성능을 보이는 것을 보임

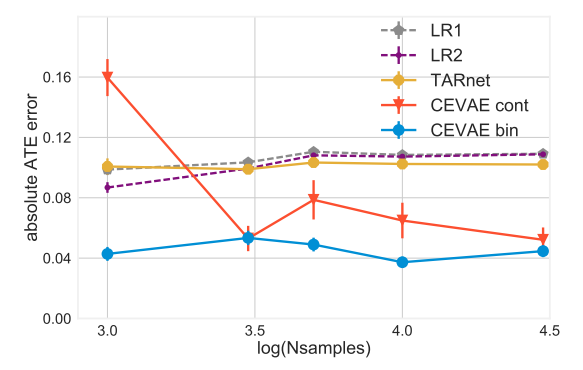
z에 대한 샘플을 많이 뽑을수록 latent space를 더 잘 표현할 수 있게 돼 error가 낮았음