인공 신경망
Neural Network
- 뉴런은 입력에 대한 선형 변환과 활성 함수activation function라 부르는 고정된 비선형 함수를 적용하는 역할을 한다.
- 여러 차원으로 가중치와 편향값을 가진 여러 개의 뉴런을 나타내므로 이 표현식은 뉴런 계층layer이라 한다.
오차 함수
- 이전의 선형 모델과 앞으로 사용할 딥러닝과의 주요 차이점은 오차 함수의 모양
- 선형 모델과 오차를 제곱한 손실 함수는 볼록 함수 형태의 오차 곡선, 최소값이 분명하게 하나로 정의.
- 신경망은 동일한 오차 제곱 손실 함수를 사용한다 하더라도 볼록 함수의 오차 곡선의 모양이 다르다.
모든 뉴런이 협력하여 유용한 출력-참값에 근사한다는 의미, 어느정도의 불완전함-을 만들기 위한 파라미터 획득을 목표로 한다.
활성 함수
- 출력 범위 제한
- 출력 범위 줄이기
- Sigmoid, tanh 등. 뉴런이 민감하게 반응하는 함수의 중앙 영역에 선형 함수 형태가 존재, 다른 영역은 경계값에 가까워짐.
신경망에서의 학습
- 심층 신경망은 고수준의 비선형적 현상에 대해
명시적 모델 없이 근사하는 능력을 부여.
훈련되지 않은 일반 모델에서 출발, 여러 입출력쌍 예제와 역전파할 손실 함수를 제공하여 일반 모델을 특정 작업에 최적화
-> 예제를 통해 일반 모델을 최적화하는 과정을 학습learning이라 한다.
torch.nn 모듈
신경망 전용 모듈, 신경망 아키텍처를 만들 수 있는 빌딩 블럭이 들어있다. 이런 빌딩 블럭을 모듈module이라 부른다.
- nn.Module의 모든 서브클래스에는 __call__ 메소드 정의되어 있고 이로 nn.Linear를 인스턴스화하여 마치 함수인 것처럼 실행 가능.
import torch.nn as nn linear_model = nn.Linear(1, 1) linear_model(t_un_val) #linear_model.forward(t_un_val) -> X
linear_model = nn.Linear(1, 1)- 인자는 입출력 크기, 편향값은 기본인 True.
- 배치 입력 만들기
- nn에 있는 모든 모듈은 한 번에 여러 입력을 가진 배치에 대한 출력을 만들도록 작성되었다.
- 배치 최적화
- 배치를 수행하는 이유는 연산량을 충분히 크게 만들어 준비한 자원을 최대한 활용하기 위함.
GPU는 병렬연산에 최적화, 여러 입력을 묶어 하나를 배치로 한 번에 실행하면 놀고 있는 다른 유닛도 계산에 사용.linear_model = nn.Linear(1,1) optimizer = optim.SGD( linear_model.parameters(), #optimizer에 선형 모델 파라미터 전달 lr=1e-2 )
- 이제 nn.Module이나 어떤 하위 모듈에 대해서도 parameters 메소드로 파라미터 리스트 얻을 수 있다.
- optimizer에는 tensor list 전달, tensor는 Parameters를 가지며 경사 하강으로 최적화될 예정이므로 requires_grad=True를 기본으로 가진다.
def training_loop(n_epochs,optimizer,model,loss_fn, t_u_train,t_u_val,t_c_train,t_c_val): for epoch in range(1,n_epochs+1): t_p_train = model(t_u_train) loss_train = loss_fn(t_p_train, t_c_train) t_p_val = model(t_u_val) loss_val = loss_fn(t_p_val, t_c_val) optimizer.zero_grad() loss_train.backward() optimizer.step() if epoch==1 or epoch%1000 ==0 : print(f"Epoch {epoch}, Training loss {loss_train.item():.4f}," f"validation loss {loss_val.item():.4f}")
- nn 자체에 손실 함수 들어있음. nn.MSELoss(). 인스턴스를 만들어 함수처럼 호출하면 된다.
linear_model = nn.Linear(1,1) optimizer = optim.SGD(linear_model.parameters(), lr=1e-2) training_loop( n_epochs = 3000, optimizer= optimizer, model = linear_model, loss_fn = nn.MSELoss(), t_u_train = t_un_train, t_u_val = t_u_val, t_c_train = t_c_train, t_c_val = t_c_val )```
신경망
이번엔 선형 모델 대신 신경망을 근사함수로 사용.
손실함수 포함 나머지 것은 그대로, model만 다시 정의.
- 선형 모듈뒤에 활성 함수 달고 다른 선형모듈에 연결
첫번째 선형+활성층은 은닉층hidden layer
->계층의 출력을 직접 관찰하는 대신 출력층의 입력으로 넣어줬기 때문- nn.Sequential 컨테이너 통해 모듈을 결합
seq_model = nn.Sequential( nn.Linear(1,13), nn.Tanh(), nn.Linear(13,1) # 앞의 13과 일치해야 한다. )
- 모델의 첫 번째 모듈은 nn.Sequential의 첫번째 인자에 해당, 중간 출력은 이어지는 다른 모듈에 전달, 최종적으로 마지막 모듈에 의해 출력이 만들어진다.
- model.paramters() 호출하면 첫,두 번째 선형 모듈에서 weight,bias 모은다.
[param.shape for param in seq_model.parameters()] ''' Out : [torch.Size([13, 1]), torch.Size([13]), torch.Size([1, 13]), torch.Size([1])] '''
- 이제 model.backward() 호출 하면 grad에서 파라미터 추출, optimizer.step() 호출 과정에서 적절하게 파라미터 값 조정.
- named_parameters() , 파라미터를 이름으로 식별 가능.
for name, param in seq_model.named_parameters(): print(name,param.shape) ''' Out : 0.weight torch.Size([13, 1]) 0.bias torch.Size([13]) 2.weight torch.Size([1, 13]) 2.bias torch.Size([1])'''
- Sequential의 각 모듈 이름은 나타난 순서 따른다.
OrderedDict 라는 인자 받는데 여기에 각 모듈의 이름을 정해서 전달가능.from collections import OrderedDict seq_model = nn.Sequential(OrderedDict([ ('hidden_linear', nn.Linear(1,8)), ('hidden+activation',nn.Tanh()), ('output_linear',nn.Linear(8,1)) ])) ''' Sequential( (hidden_linear): Linear(in_features=1, out_features=8, bias=True) (hidden+activation): Tanh() (output_linear): Linear(in_features=8, out_features=1, bias=True) ) '''for name, param in seq_model.named_parameters(): print(name,param.shape) ''' hidden_linear.weight torch.Size([8, 1]) hidden_linear.bias torch.Size([8]) output_linear.weight torch.Size([1, 8]) output_linear.bias torch.Size([1]) '''
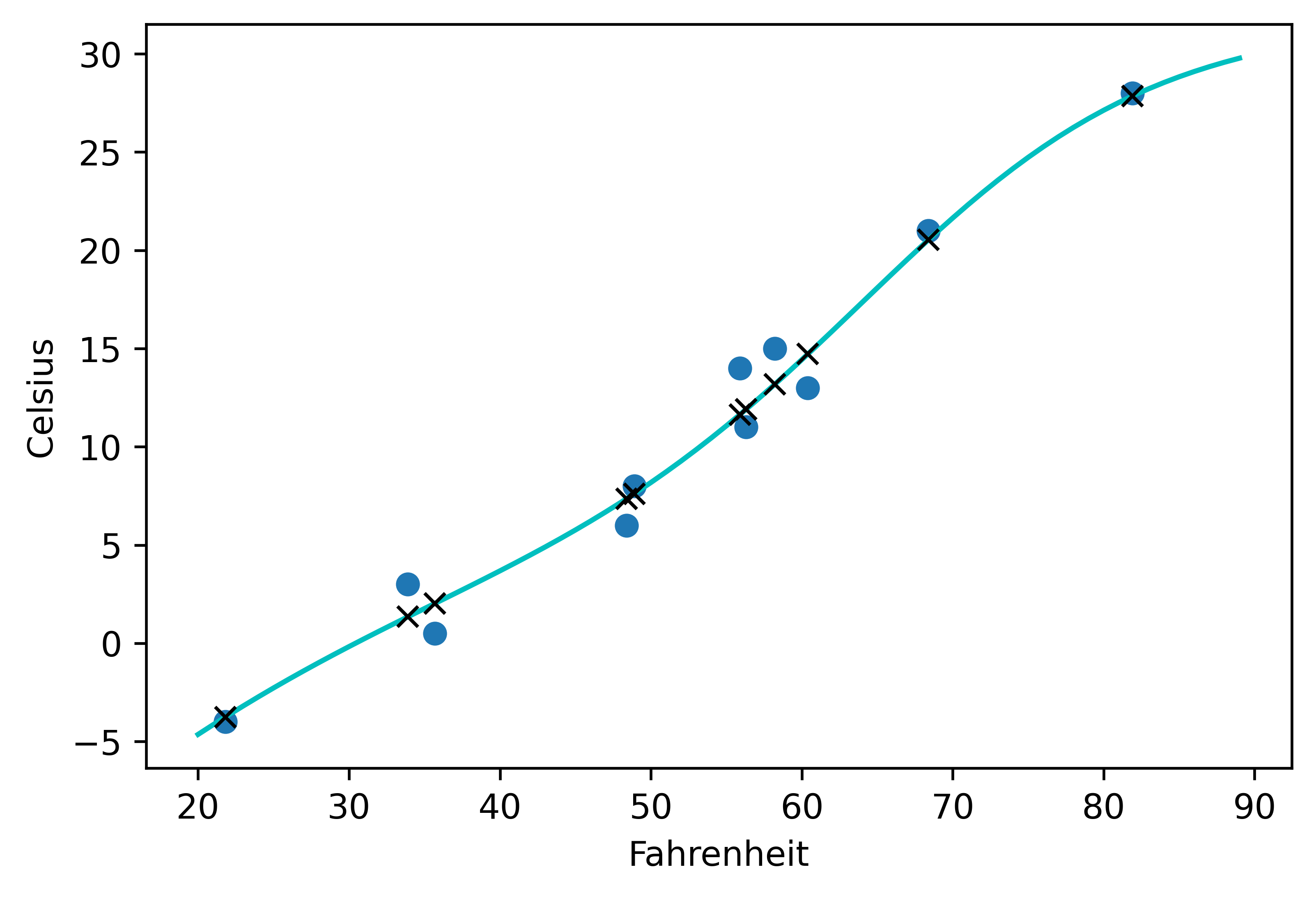
- 선형 모델과 비교
- 입력은 o, 출력은 x
from matplotlib import pyplot as plt t_range = torch.arange(20.,90.).unsqueeze(1) fig = plt.figure(dpi=600) plt.xlabel("Fahrenheit") plt.ylabel("Celsius") plt.plot(t_u.numpy(), t_c.numpy(), 'o') plt.plot(t_range.numpy(), seq_model(0.1*t_range).detach().numpy(), 'c-') plt.plot(t_u.numpy(), seq_model(0.1*t_u).detach().numpy(), 'kx')
- 신경망이 노이즈까지 포함해서 측정값을 과도하게 따라가는 과적합 성향 보인다.
- 과적합을 방지 하기 위해선, 더 많은 데이터를 구하거나, 데이터가 더욱 다양한 값을 가지게 하던가, 더 단순한 모델을 사용하는 방법 등을 시도한다.