1. Binary Search 이진 탐색
문제: 크기가 n인 정렬된 배열 S에 x가 있는지 결정하라.
입력: 자연수 n, 비내림차순으로 정렬된 배열 S[1...n], 찾고자 하는 항목 x
출력: locationout
x가 배열 S에 있는 경우: x의 위치
x가 배열 S에 없는 경우: 0
- 알고리즘
- x가 배열의 중간에 위치한 항목과 같으면 -> x 찾음
그렇지 않으면: - Divide(분할): 배열을 반으로 나누어서 x가 중앙에 위치한 항목보다 작으면 왼쪽의 서브배열을 선택, x가 더 크면 오른쪽 서브배열을 선택한다.
- Conquer(정복): 선택된 서브배열에서 x를 찾는다.
- x가 배열의 중간에 위치한 항목과 같으면 -> x 찾음
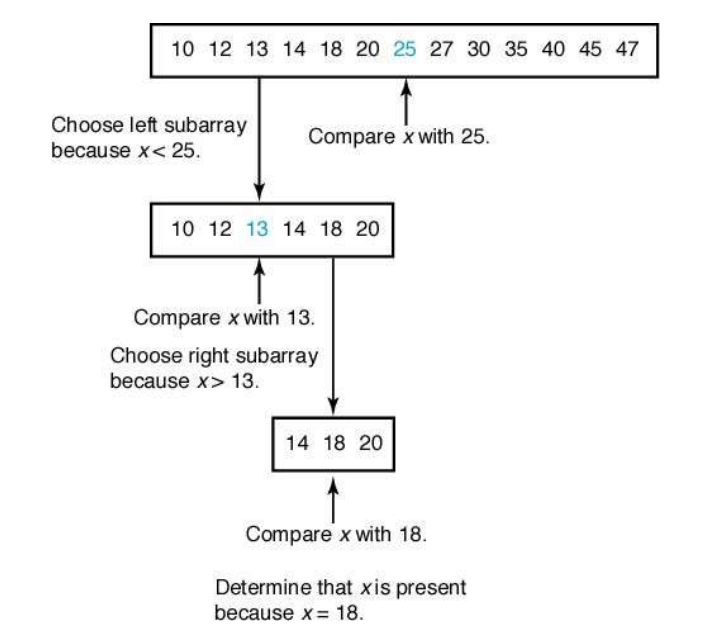
찾고자 하는 항목 x = 18일 때, 배열에서 x를 찾는 과정을 그림으로 표현한 것이다.
맨 처음 배열의 중앙에 위치한 25와 비교하고, 18은 25보다 작기 때문에 왼쪽의 서브 배열인 [10 12 13 14 18 20]을 선택한다.
이번에는 서브배열 [10 12 13 14 18 20]의 중앙에 위치한 13과 비교한다. 18은 13보다 크기 때문에 이번에는 오른쪽 서브배열인 [14 18 20]을 선택한다.
[14 18 20]의 중앙에 위치한 18과 비교한다. 우리가 찾고자 하는 항목 x=18과 일치하므로 검색이 종료된다.
- 중앙에 위치한 항목을 구하는 방법 (배열의 인덱스를 1...n이라고 가정한다.)
배열의 길이가 짝수인 경우: n/2번째 위치한 항목이 mid이다.
배열의 길이가 홀수인 경우: (n-1)/2번째 위치한 항목이 mid이다.
2. psuedocode, 꼬리재귀
index location(index low, index high){
index mid;
if(low > high) return 0;
else{
mid = ┗ (low + high) / 2 ┛; // 정수 나눗셈
if(x == S[mid]) return mid; // x 찾음
else if(x < S[mid]) location(low, mid-1); // 왼쪽 서브 배열 선택
else location(mid+1, high); // 오른쪽 서브 배열 선택
}
}왜 n, S, x는 지역변수로 사용하지 않는가?
n, S, x는 각 재귀 호출마다 변하지 않고 유지되는 값이다. 만약 재귀 안에 지역 변수로 만들어서 사용한다면, 재귀 호출할 때마다 스택에 값이 할당되고 메모리가 낭비된다. 따라서 재귀 호출 안에서 바뀌는 값이 아니라면 전역변수로 사용하는 것이 훨씬 효율적이다.
꼬리 재귀 (tail-recursive)
- 재귀 호출이 끝나면 다른 연산을 수행하지 않고 결과를 return하는 일만 남아있는 재귀를 꼬리재귀라고 한다.
꼬리재귀 대신 Iterative를 사용한다면?
- 스택을 제거하여 상당한 양의 메모리를 절약할 수 있다.
- 스택을 유지 관리할 필요가 없기 때문에 반복 알고리즘이 더 빨리 실행된다.
