알고리즘

아래로 갈수록 성능이 최악이다.그림에는 없지만 theta(n^n)의 성능이 가장 안 좋다. 정의: 점근적 상한(Aymptotic Upper Bound)주어진 복잡도 함수 f(n)에 대해서 g(n)∈O(f(n))이면 다음을 만족한다.For a given complexit

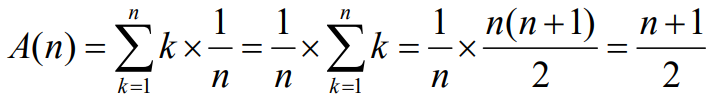
문제: 크기가 n인 배열 S에 x가 있는가?입력 파라미터: (1) 양수 n, (2) 배열 S1...n, (3) 키 x출력: x가 배열 S에 있는 경우 -> x의 위치x가 배열 S에 없는 경우 -> 0알고리즘x와 같은 값을 찾을 때까지 S에 있는 모든 아이템을 순서대로

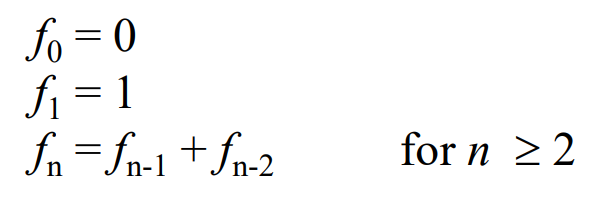
피보나치 수열의 정의예: 0, 1, 1, 2, 3, 5, 8, 13, 21, ...피보나치 수열의 n번째 값을 찾는 알고리즘입력: n출력: 피보나치 수열의 n번째 값fibo(5)의 재귀 트리n=0, fibo(0) = 1n=1, fibo(1) = 1 이면 n>=2에서 f

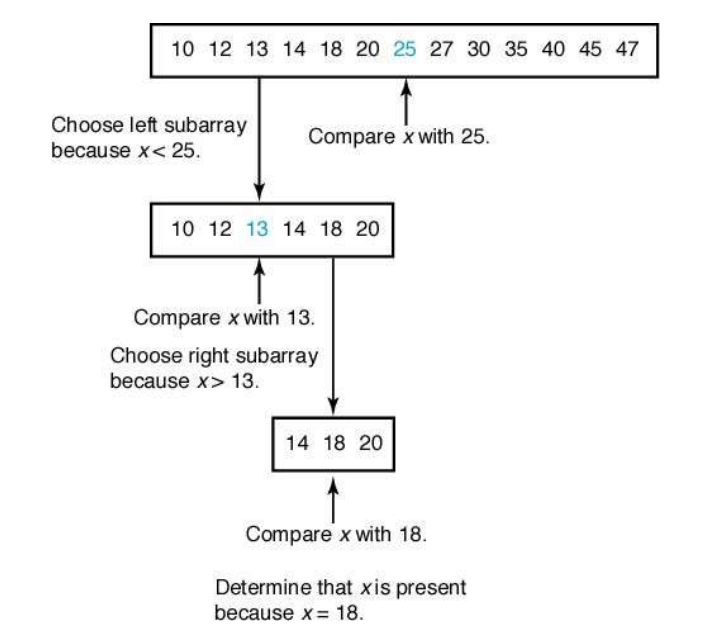
문제: 크기가 n인 정렬된 배열 S에 x가 있는지 결정하라.입력: 자연수 n, 비내림차순으로 정렬된 배열 S1...n, 찾고자 하는 항목 x출력: locationoutx가 배열 S에 있는 경우: x의 위치x가 배열 S에 없는 경우: 0알고리즘x가 배열의 중간에 위치한

분할(divide)해결하기 쉽도록 문제를 여러 개의 작은 부분으로 나눈다.정복(Conquer - Solve)나눈 작은 문제를 각각 해결한다.통합(Combine - Obtain the solution)필요하다면 해결된 해답을 모은다.Top-down approach(하향식

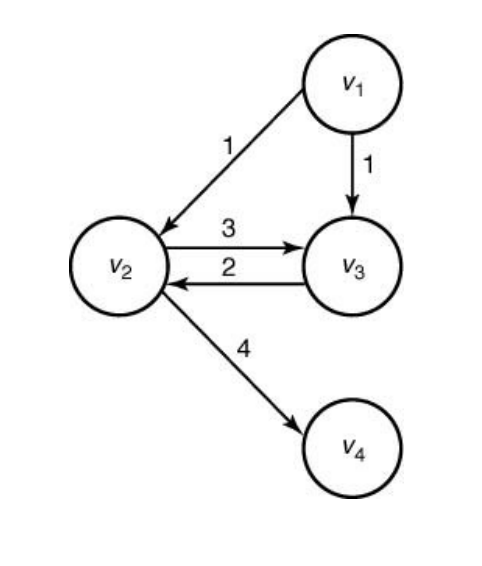
주어진 문제에 대하여 하나 이상의 많은 해답이 존재할 때, 그 중에서 가장 최적인 해답(optimal solution)을 찾는 문제를 최적화 문제라고 한다.최단경로 찾기 문제가 최적화 문제의 대표적인 예시이다.어떤 문제의 입력에 대한 최적 해가 그 입력을 나누어 쪼갠