1. Fibonacci Sequence (피보나치 수열)
- 피보나치 수열의 정의
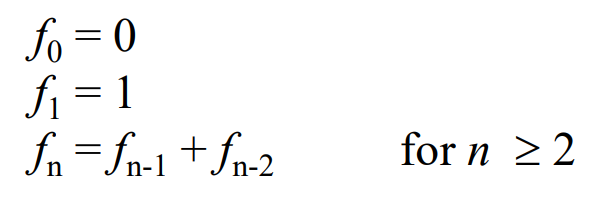
- 예: 0, 1, 1, 2, 3, 5, 8, 13, 21, ...
2. 피보나치 수 구하기 알고리즘 (Recursive)
- 피보나치 수열의 n번째 값을 찾는 알고리즘
- 입력: n
- 출력: 피보나치 수열의 n번째 값
pseudocode
int fibo(int n){
if(n <= 1)
return n;
else
return fibo(n-1) + fibo(n-2);
}- fibo(5)의 재귀 트리
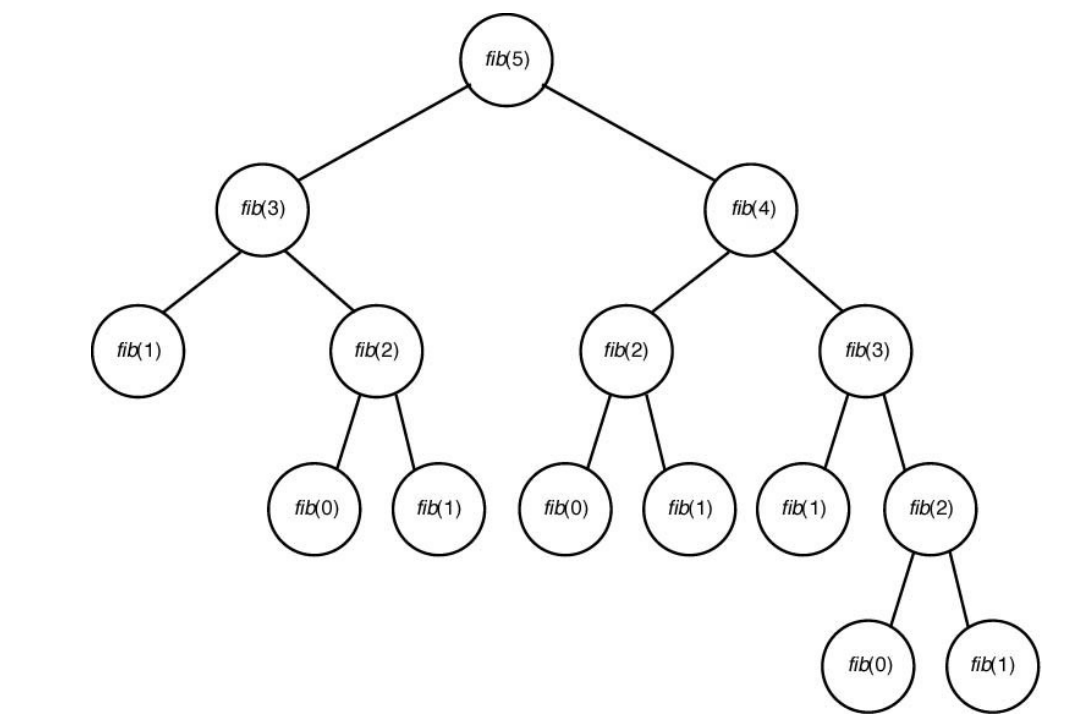
n=0, fibo(0) = 1
n=1, fibo(1) = 1 이면
n>=2에서 fibo는 2, 3, 5, 8 ...이 된다. 즉 n=5일 때 fibo=8이다. 이 값은 fibo(5)의 재귀 트리 그림에서 말단 노드의 개수와 같다.
n=3일 때도 fibo(3) = 3이고, fibo(3)의 말단 노드도 fibo(1), fibo(0), fibo(1)으로 3개라는 것을 알 수 있다. 이 때 말단 노드의 개수는 fib(n)을 계산하기 위하여 fib 함수를 호출하는 횟수라고 할 수 있다.
T(n) = fib(n)을 계산하기 위하여 fib 함수를 호출하는 횟수 = 재귀 트리의 말단 노드 개수

3. 피보나치 수 구하기 알고리즘 (Iterative)
pseudocode
int fibo2(int n){
index i;
int f[0...n];
f[0]=0;
if(n > 0){
f[1] = 1;
for(i = 2; i<=n; i++)
f[i] = f[i-1] + f[i-2];
}
}- Dynamic Programming, Bottom-Up
- 중복 계산이 없기 때문에 재귀보다 훨씬 빠르다.
- 계산하는 항의 총 개수 T(n) = n + 1
- f[0]부터 f[n]까지 한 번씩만 계산(계산한 값을 배열에 저장해두고 필요할 때마다 꺼내서 사용한다.)
4. 피보나치 문제를 해결할 때, Recursive와 Iterative 중 더 효율적인 것은?
- 피보나치 수열 문제는 Divide&Conquer 방법으로 해결하면 중복 계산이 발생하기 때문에 Dynamic Programming 기법으로 푸는 것이 더 효율적이다.
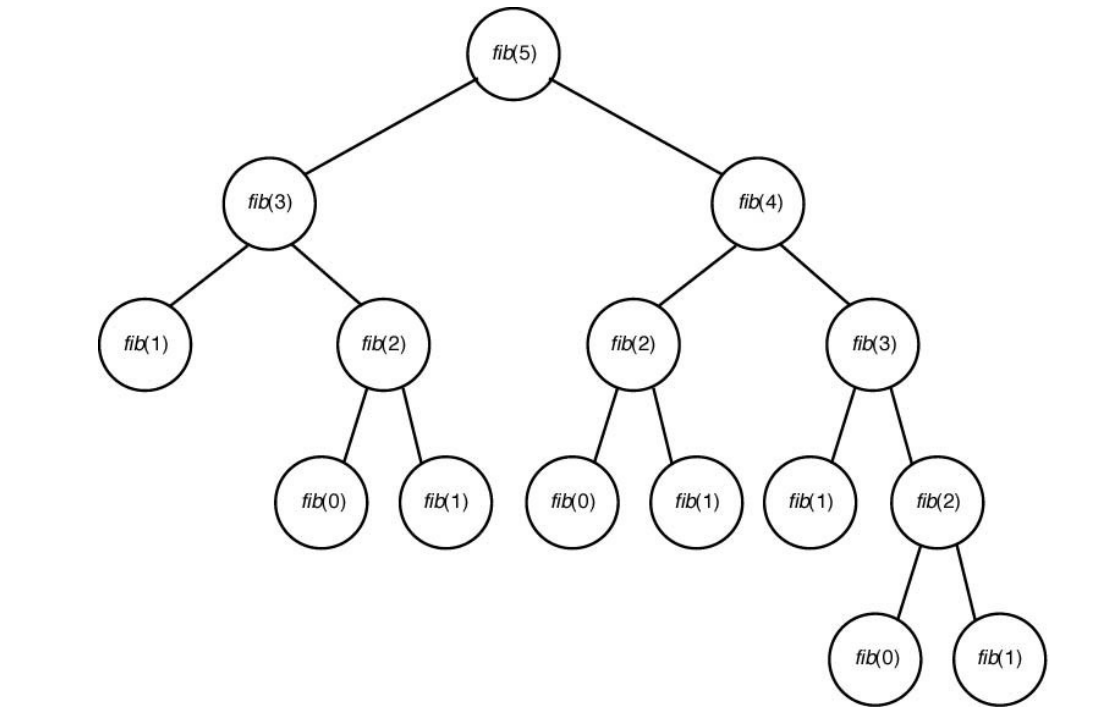
위 그림은 피보나치의 재귀 트리이다.
Recursive 방법이 비효율적인 이유를 fib(2)의 중복 계산으로 알아보자.
(그림 참고) fib(4)를 구하기 위해서 fib(2)는 fib(2)를 구할 때 +1번, fib(3)을 구하기 위해 fib(2)를 호출할 때 +1번. 총 두 번의 중복 계산이 발생한다.
하지만 Iterative 방식으로 문제를 해결한다면 for문을 통해 fib(2) 값을 배열에 저장해두고 필요할 때마다 값을 가져와서 사용하기 때문에 중복 계산이 발생하지 않고 수행속도가 훨씬 빠르다. 따라서 Recursive보다 Iterative 방식이 더 효율적이라고 할 수 있다.
