1. Sequential Search (순차 탐색)
- 문제: 크기가 n인 배열 S에 x가 있는가?
- 입력 파라미터: (1) 양수 n, (2) 배열 S[1...n], (3) 키 x
- 출력:
x가 배열 S에 있는 경우 -> x의 위치
x가 배열 S에 없는 경우 -> 0
- 알고리즘
- x와 같은 값을 찾을 때까지 S에 있는 모든 아이템을 순서대로 검사한다.
- x와 같은 값을 찾으면 S 안에서의 위치 값을 전달한다.
- x와 같은 값을 찾지 못하면 0을 전달한다.
2. pseudocode
void seqsearch(int n, const keytype S[], keytype x, index& location){
location = 1;
while(location <= n && S[location] != x)
location ++;
if(location > n)
location = 0;
}- location 변수를 사용하여 S[1]부터 x를 찾을 때까지(x가 없다면 배열 끝까지) 탐색한다.
- while문: 아직 탐색할 항목이 남아 있는지, x를 찾지 못했는지
- x를 찾지 못했다면 location이 n일 때(배열 끝까지 도달했을 때) location++;이 작동하고 while문이 끝났을 때 location은 n보다 큰 값일 것이다.
- if문: 배열 끝까지 검색했지만 x를 찾지 못했는지
3. 분석
-
E(n): 입력 값인 배열의 길이 n에 따라 검색 횟수가 달라지므로 every case를 구할 수 없다.
-
B(n): S[1]이 x인 경우, B(n)=1
-
W(n): 배열 안에 x가 없는 경우 or 배열의 마지막 원소가 x인 경우. 즉, 배열의 끝까지 전부 탐색한 경우 W(n) = n
-
A(n)
-
경우 1. x가 배열에 확실히 있는 경우만 고려
1 <= k <= n일 때, x가 배열의 k위치에 있을 확률은 1/n이다.
x가 배열의 k번째에 있다면 x를 찾기 위해 실행되는 단위 연산의 횟수는 k이다.
따라서,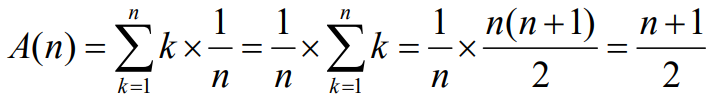
-
경우 1. x가 배열에 없는 경우도 고려
x가 배열 S에 있을 확률을 p라고 할 때, 배열에 없을 확률은 (1-p)이고, x가 배열의 k번째에 있을 확률은 p/n이다. 따라서,
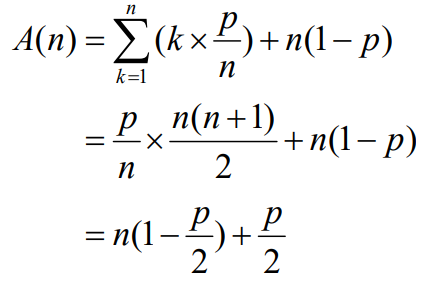
-
