(고수B) 7. 중적분

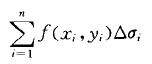
본 포스트는 작성자가 중국 북경대학교에서 22-23학년도 2학기 고등수학B(2) 수업을 들으며 배운 내용을 복습하며 정리한 포스트입니다. 중국어, 한국어, 영어가 뒤섞인 본인이 알아보기 위해 작성한 필기를 정리하는만큼 다른분들이 읽기엔 조금 불친절할수 있습니다.

고수 상을 무사히 넘긴 여러분, 축하드립니다!
이젠 적분을 두번, 아니 세번까지 할 차례다!

7.1. 이중적분의 개념과 성질

개념은 간단하다. $z=f(x,y)$가 유계구역 D 안에서의 함수라면, D를 $D_1,D_2...$의 구역으로 나누고 위의 함수가 어떤 x와 y에 대해서도 극한이 존재한다면, 이를 $f(x,y)$의 D 위에서의 이중적분이라 부른다. 이중 $\sigma_i$는 $D_i$의 면적을 뜻한다.

7.2. 이중적분의 계산

가장 중요한 부분이다.

일반적인 계산

기본적으로 이중적분을 연속된 두개의 정적분으로 변환시켜 계산한다 생각하면 된다.

이렇게. 어떻게 이리 되냐 하면,

이런식으로 D를 $x=a$, $x=b$ $(a<b)$와 곡선 $y=\varphi_1(x)$, $y=\varphi_2(x)$ $(\varphi_1(x)<\varphi_2(x))$두개의 곡선으로 둘러싸였다고 하면 위처럼 변한다. 위의 그림 7.4에서 보이듯, 이는 $z=f(x,y)$를 顶으로 두고, 구역 D를 底로 두는 柱体의 부피와 같다.


교과서의 예시들이다. 바운더리를 잘 잡는게 중요하다. 아니면 계산 시작 자체가 불가능하니!

극좌표에서의 계산

$x,y$좌표로 말고, $\theta, r$좌표로 바꿔서 계산하는 법이다. 자세한 증명과정은 교과서에 나와있고, 결론적으로 보면

위와 같은 형식으로 계산하게 된다. 여기에서 r을 빼먹는 실수를 하면 안된다.


교과서 예제문제 풀이다. 마지막 적분공식은 나중에 유용할거라고 한다.

一般变量替换公式

위의 공식을 이용한다. 예제를 보자.

마지막 동그라미 친 부분은 广义极坐标变换으로도 알려져서 자주 쓰인다.

对称性의 응용

1중적분일때를 복습해보면, f(x)가 偶函数 ($f(x)=f(-x)$)라면 위처럼 반갈죽해서 계산이 가능했고, 奇函数라면 ($f(-x)= - f(x)$) 0임을 알 수 있었다. 이중적분도 비슷하다.

우선 이원함수에서

• $f(x,-y)=f(x,y)$일 시 $f(x,y)$가 $y$에 대해 偶函数라고 하고, 이때 함수의 모양 은$O_(zx)$ 평면에 대칭한다. $f(-x,y)=f(x,y)$일 시에 는 반대로 $f(x,y)$가 $x$에 대해 偶函数이고, $O_(yz)$평면에 대칭한다.

• $f(x,-y)=-f(x,y)$일 시 $f(x,y)$가 $y$에 대해 寄函数라고 하고 $f(-x,y)=-f(x,y)$일 시 $f(x,y)$가 $x$에 대해 寄函数라고 한다.
  
  이제 이 개념을 응용해보면:

• 그림 7.9처럼 x축에 대해 적분 구역이 대칭하다면, $f(x,y)$가 $y$에 대해 偶函数라면 (1)처럼 구역을 나눠서 적분 계산이 가능하다. 만약 $y$에 대해 奇函数라면 적분의 값은 0이 된다.

• 그림 7.10처럼 y축에 대해 적분 구역이 대칭하다면, $f(x,y)$가 $x$에 대해 偶函数라면 (2)처럼 구역을 나눠서 적분 계산이 가능하다. 만약 $x$에 대해 奇函数라면 적분의 값은 0이 된다.

7.3 삼중적분

하다못해 이젠 적분을 3번한다.

일반적인 계산

적분을 3번 하는 식으로 나눌건데, 3번이기 때문에 방법이 크게 두가지로 갈린다.

첫번째 방법은 무난하게, 우선 z에 대해 범위를 잡고 적분하고 그후에 x와 y에 대해 하는방법이다. (선 1중적분->후 이중적분)

예시다. z를 기준으로 우선 적분하고, x와 y를 나눠서 했다.

두번째 방법은 접근법을 약간 바꿔, 밑의 넓이에 대해 이중적분을 하고 그 넓이만큼 쫘앜 늘려서 적분해 부피를 구하는 법이다. (선 2중적분->후 1중적분)

예시다. $x^2+y^2=1$을 밑면적으로 잡고, z축 0에서부터 1까지 올라가는 방식이다. 밑면적의 반경이 $\sqrt z$이기 때문에 ($z=x^2+y^2, \sqrt (x^2+y^2) < \sqrt z$), 바로 넓이인 $\pi z$를 곱하면 2중적분이 완료된다.

극좌표에서의 계산

극좌표에서도 위처럼 두가지 방법으로 갈린다.

기본 공식이다. z를 그대로 두는거 외엔 크게 다를 게 없다.

첫번째 방법은 비슷하게, z에 대해 먼저 적분하고 하는 방식이다.

두번째 방법도 xy좌표에서와 비슷하게 넓이를 구하고 $\theta$에 대해 늘리는 방법이다.

球坐标에서의 계산

공식을 외우자.

对称性의 응용

3중적분에도 있다.

• $f(x,y, -z)=-f(x,y,z)$일 시 $f(x,y,z)$가 $z$에 대해 奇函数라고 하고 적분구역이 $O_(xy)$에 대해 대칭하다면 적분값은 0이 된다.

• $f(x,y, -z)=f(x,y,z)$일 시 $f(x,y,z)$가 $z$에 대해 偶函数라고 하고 이때는 적분을 위처럼 2개로 나누어 계산이 가능하다. 나머지 경우도 충분히 类推가능.