최근 GAN을 사용하며 손실함수에 대한 증명을 소홀히 하지 않았나 생각했다.
이번 주말 원 논문을 다시 정독하며 손실함수에 대한 증명을 다시 진행하고 기록을 남긴다.
손실 함수에 대한 수렴증명은 다시 봐도 완벽하게 이해되지 않는다. 더 많은 학습이 필요하다.
ps. 잘못된 내용이 있다면 댓글을 남겨주시면 바로 반영하겠습니다.
Generative Adversarial Networks loss 및 증명
Ian Goodfellow가 처음 제안했던 GAN은 생성자 및 분류자 두 모델이 경쟁하면서 생성자 모델의 데이터 생성 능력을 개선한다. 생성자는 분류자가 진짜(1)로 인식하게끔 학습이 이루어지고 분류자는 실제 데이터는 진짜(1)로 인식하며 생성자에서 생성되는 이미지는 가짜로 인식하게끔 학습이 이루어진다.
원 논문에서 제안된 학습 알고리즘은 아래와 같다.

GAN의 손실함수는 아래와 같은 형태로 생성자(G), 분류자(D)의 minmax 경쟁 학습으로 실제 데이터와 생성 데이터인 분포( pdata,pg)가 같은 해를 찾도록 학습이 진행된다.
GminDmax V(D,G)=Ex∼pdata(x)[logD(x)]+Ez∼pZ(z)[log(1−D(G(z)))])
GAN논문에서는 2가지를 증명한다.
1. Pdata=Pg 가 global optimum 인가?
2. Convergence of Algorithm 1
Pdata=Pg 가 global optimum 인가?
Proposition
- 고정된 생성자(G)에 대해서 최적의 분류자(D)는 다음과 같다.
DG∗(x)=Pdata(x)++Pg(x)Pdata(x)
고정된 생성자 G가 주어지면 분류자 D에 대한 V(D)를 아래와 같이 나타날 수 있다. 이는 기댓값의 정의 식(link)을 통해 적분식으로 다시 나타낼 수 있다.
Dmax V(D)===Ex∼pdata(x)[logD(x)]+Ex∼pg(x)[log(1−D(x))])∫xpdata(x)log(D(x))dx+∫xpg(x)log(1−D(x))dx∫x(pdata(x)log(D(x))dx+pg(x)log(1−D(x)))dx
식을 정리하면 결국 적분식을 최대화(max)하는 것을 확인할 수 있다.
여기서 Pdata(x),Pg(x),D(x)를 a,b,y로 나타내면 적분식 내부는 아래와 같은 형태로 나타낼 수 있다. y인 분류자는 sigmoid 함수를 사용하기 때문에 출력 값이 0에서 1이 범위를 가지게 된다.
pdata(x)log(D(x))dx+pg(x)log(1−D(x))pdata(x)→apg(x)→bD(x)→yy∈[0,1]y→alog(y)+blog(1−y)
직관적인 이해를 위해 alog(y)+blog(1−y)에서 a:1, b:1을 놓고 그려보면 아래와 같은 plot을 확인할 수 있다. 따라서 식은 0.5에서 최댓값을 가지게 되며 y=a+ba 에서 최댓값을 가지는 것을 알 수 있다.
때문에 제안했던 위 수식에 따라 DG∗(x)=Pdata(x)++Pg(x)Pdata(x) 이라는 식이 성립하게 된다.
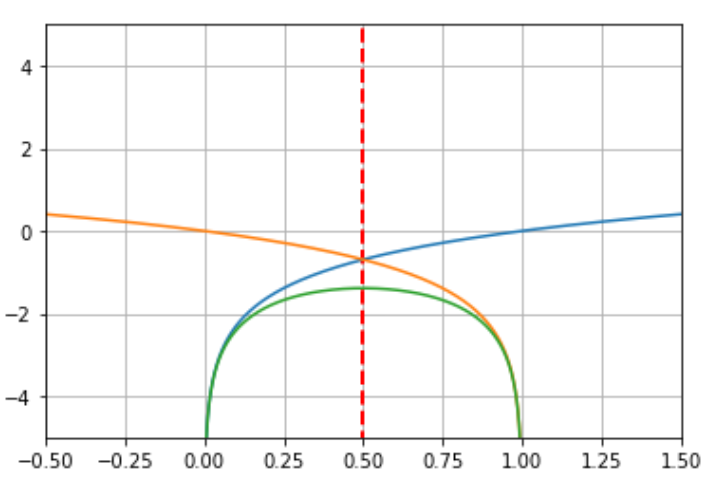
푸른색은 : log(y)
주황색은 : log(1-y)
초록색은 : log(y) +log(1-y)
을 나타낸다.
위 수식에 대한 최댓값을 미분을 통해 확인하면 다음과 같다.
f(x)=alog(x)+blog(1−x)dxf(x)====xa−1−xb=0a(x−1)+bx=0(a+b)x−a=0(a+b)x=ax=a+ba
생성자의 global optimum는 분류자가 잘 학습된 pdata=pg 인 경우 달성된다. 그 때 생성자의 평가값인 C(G)는 -log4를 보이게 된다. C(G)를 나타내면 아래와 같은 식으로 풀 수 있다.
C(G)==DmaxV(G,D)Ex∼pdata(x)[log(D(x))]+Ez∼pZ(z)[log(1−D(G(z)))])
위 식을 D가 최적일 때 즉 DG∗(Pdata(x)++Pg(x)Pdata(x))로 다시 나타내면 아래와 같이 풀어 낼 수 있다.
C(G)===Ex∼pdata[log(DG∗(x))]+Ez∼pZ[log(1−DG∗(G(z)))])Ex∼pdata[log(DG∗(x))]+Ex∼pg[log(1−DG∗(x))])Ex∼pdata[log(pdata+pg(x)pdata(x))]+Ex∼pg[log(pdata+pg(x)pg(x))])
증명의 편의성을 위해 여기에서 log(4)를 식에 추가한다.
C(G)=Ex∼pdata[log(pdata+pg(x)2∗pdata(x))]+Ex∼pg[log(pdata+pg(x)2∗pg(x))])−log(4)
식을 여기까지 풀어내면 이제 Kullback–Leibler divergence(KLD) 그리고 Jenson-Shannon divergence(JSD) 가 등장한다.
KLD는 어떤 두 확률분포의 차이를 계산을 하기위해 사용되는 함수로, 대표적으로 다음 두 가지 특징이 있다.
- KL(P∣Q)≥0
- KL(P∣∣Q)=KL(Q∣∣P) (때문에 거리가 아니다.)
증명을 위한 KLD, JSD의 내용만 간략하게 설명하면
어떠한 확률분포 P, Q 가 있을때 두 확률분포의 KLD는 다음과 같이 표현 할 수 있다.
KL(P∣∣Q)==Ex∼P[log(Q(x)P(x))]=Ex∼P[−log(P(x)Q(x))]x∑P(x)log(Q(x)P(x))=−x∑P(x)log(P(x)Q(x))
KLD를 이해했다면 JSD는 더욱 간단하게 표현할 수 있다.
JSD(P∣∣Q)=21KL(P∣∣M)+21KL(Q∣∣M)where,M=21(P+Q)
그럼 다시 수식을 KLD로 나타내면 다음과 같다.
C(G)==Ex∼pdata[log(pdata+pg(x)2∗pdata(x))]+Ex∼pg[log(pdata+pg(x)2∗pg(x))])−log(4)−log(4)+KL(pdata∣∣2pdata(x)+pg(x))+KL(pg∣∣2pdata(x)+pg(x))
이 수식은 한번 더 JSD로 표현할 수 있다.
C(G)===−log(4)+KL(A∣∣M)+KL(B∣∣M)where,A=pdata(x),B=pg(x),M=2pdata(x)+pg(x)−log(4)+2∗JSD(A∣∣B)−log(4)+2∗JSD(pdata∣∣pg)
JSD는 최적인 상황일때 즉 pdata=pg 일때 0이 되므로 -log(4)의 global optimum 지점에 도달 할 수 있다.
Convergence of Algorithm 1
학습 알고리즘이 이 문제를 수렴시킬 수 있는지를 정명
Proposition
- 생성자와 분류자가 충분한 용량 (파라미터)를 가지고 있다고 가정한다.
- Alhorithm 1의 각 단계에 있을 때, 분류자는 생성자가 최적의 해를 가지도록 만들어 주고
- pg는 다음 손실을 향상 시키는 방향으로 업데이트되어 pdata로 수렴
V(G,D)=U(pg,D)를 pg에 대한 함수로 생각 U(pg,D)는 pg에 대해 convex 함수
convex function: 볼록 함수
임의 두 점을 이은 선이 두 점을 이은 곡선보다 위에 있는 함수
최적의 D에서 pg에 대한 gradient descent update로 pg를 pdata에 수렴할 수 있다.
실제로 적대적 네트워크는 생성자인 G(z;θg)를 통해 제안된 집합인 pg분포를 나타내며, 생성자의 학습 즉 생성자의 가중치인 θg의 최적화를 진행한다. 신경망의 우수한 성능은 이론적 보장이 부족함에도 합리적인 모델을 만들어 낼 수 있게 된다.
참조


