특이값 분해(SVD, Singular Value Decomposition)
일반적인 m×n 행렬에 관한 행렬 분해
LU분해, QR분해 ⇒ n×n 정방행렬에 대한 행렬분해
특이값 분해는 직교분할, 확대축소, 차원변환 등과 관련이 있다.
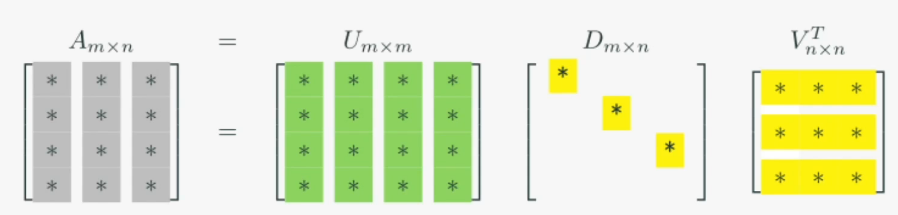
U:m차원 회전행렬(정규직교행렬)
D:n차원 확대축소(확대축소 크기에 따른 정렬 형태
V:n차원 회전행렬(정규직교행렬)
주성분분석(PCA, Principal Component Analysis)
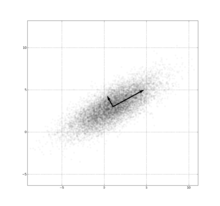
데이터의 공분산행렬에 대한 고유값 분해에 기반을 둔 직교분해
K개의 n차원 데이터 {xi}i=1K가 있을 때, 데이터의 중심 m과 공분산행렬 C는 다음과 같다.
m=K1i=1∑Kxi,C=K1i=1∑K(xi−m)(xi−m)T
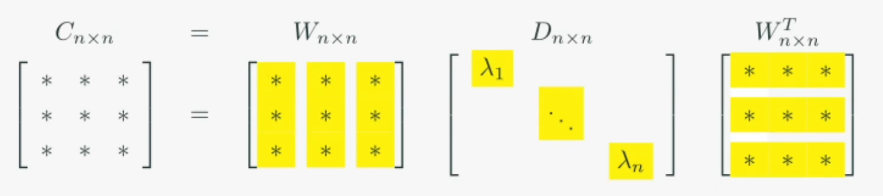
W:n차원 회전행렬(정규직교행렬)
D:n차원 확대축소(확대축소 크기에 따른 정렬 형태)
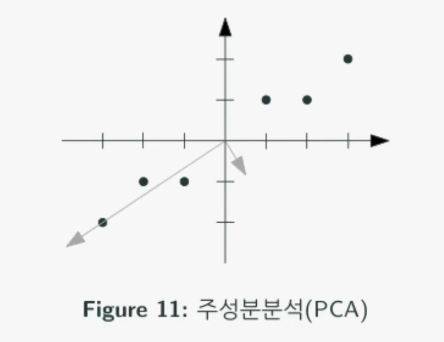

[11]에서 내적하여 [11] [11]=[1111]를 구한다.
모든 점에 대한 내적을 더해 평균을 하면 공분산행렬 C를 구할 수 있다.




