벡터공간과 최소제곱법

열공간
행렬 $A$의 열벡터들에 대한 가능한 모든 선형조합의 결과를 모아 집합으로 구성한 것

선형시스템 $Ax = b$가 해를 가지면 $b \in col(A)$
해를 가지지 않으면 $b \notin col(A)$

선형시스템 $Ax = b$의 해가 없는 경우 할 수 있는 최선은 무엇인가?
행렬 $A$가 정의하는 열공간에서 우리의 목표 $b$와 가장 가까운 지점은 $b$를 열공간에 투영한 점일 것이다.

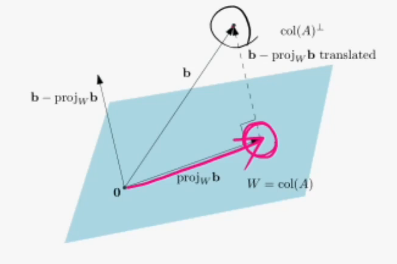
최소제곱법(Least Squares Method)
선형시스템 $Ax = b$에 대한 해 $x$가 없음에도 불구하고, 할 수 있는 최선의 대안 $\bar{x}$를 내놓는 기법
최소제곱법은 원래의 선형시스템 $Ax = b$가 아닌 $A\bar{x} = \bar{b} \,\,\,\,\, (\bar{b} =proj$ $_Wb)$
이 방법은 목표 $b$와 달성가능한 목표 $\bar{b}$의 차이를 나타내는 벡터 $(b - \bar{b})$의 제곱길이를 최소화시키는 의미를 가지기 때문에 최소제곱법이라 한다.

최소제곱법으로 구한 해 $\bar{x}$는 원래의 선형시스템을 만족하는 해가 아니다.
$A\bar{x} \neq b$

최소제곱법으로 구한 해 $\bar{x}$는 $b$의 근사해이다.
$A\bar{x} = proj$$_Wb$

최소제곱법의 응용 : 선형회귀(Linear Regression)
2차원 공간에 m개의 정점 ${(x_i, y_i)}_{i=1}^m$이 그림과 같이 있을 때, 이를 잘 설명할 수 있는 직선 $y = mx + b$를 구하는 문제를 선형회귀 문제라 한다.

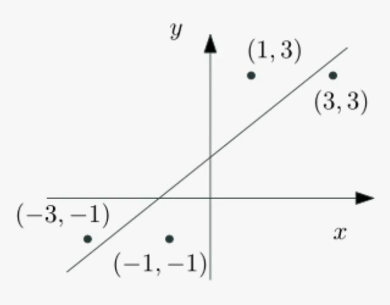
선형회귀 문제는 다음과 같이 최소제곱법으로 풀 수 있다.
1. 선형시스템 구성
직선이 각 정점을 모두 지나간다고 가정하고 선형시스템 $Ax = b$ 구성 (단, 주어진 모든 정점을 지나가는 직선은 존재하지 않으므로 선형시스템의 해는 존재하지 않음.)
$y = mx + b \to \begin{bmatrix} -3 & 1 \\ -1 & 1 \\ 1 & 1 \\ 3 & 1 \end{bmatrix} \begin{bmatrix} m \\ b \end{bmatrix} = \begin{bmatrix} -1 \\ -1 \\ 3 \\ 3 \end{bmatrix}$
2. 최소제곱법 적용
$A^TA\bar{x} = A^Tb$를 생각하고 $\bar{x} = \begin{bmatrix} \bar{m} \\ \bar{b} \end{bmatrix}$를 구한다.