SSD (2016.11)

2016년 11월 논문 출시(https://arxiv.org/pdf/1512.02325.pdf)

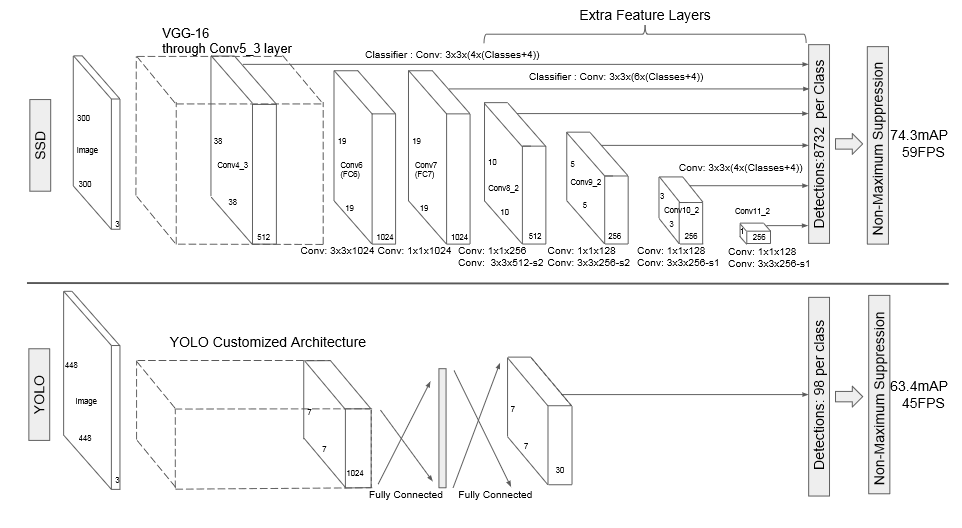
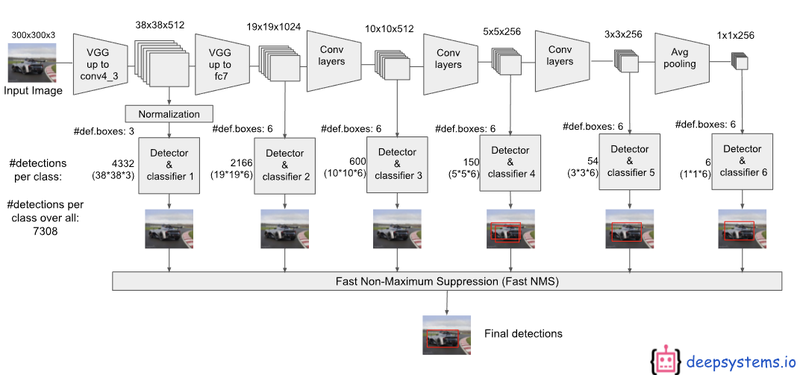
SSD Network 구조

• FeatureMap
• AnchorBox를 기반으로 Classification & Detection

SSD 주요 구성 요소

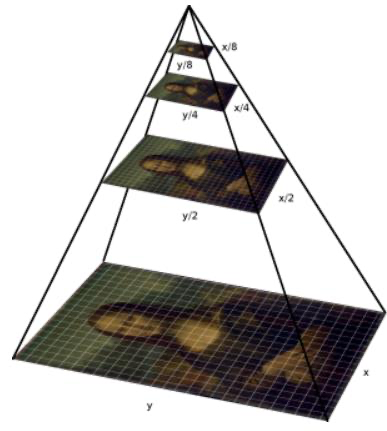
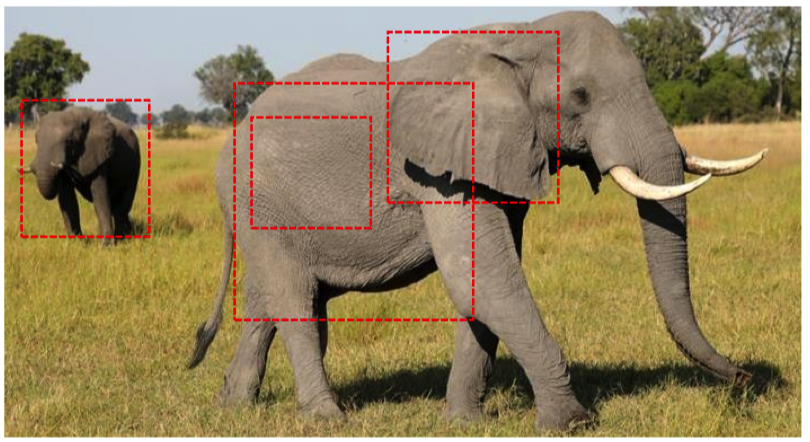
이미지 Scale 조정에 따른 여러 크기의 Object Detection

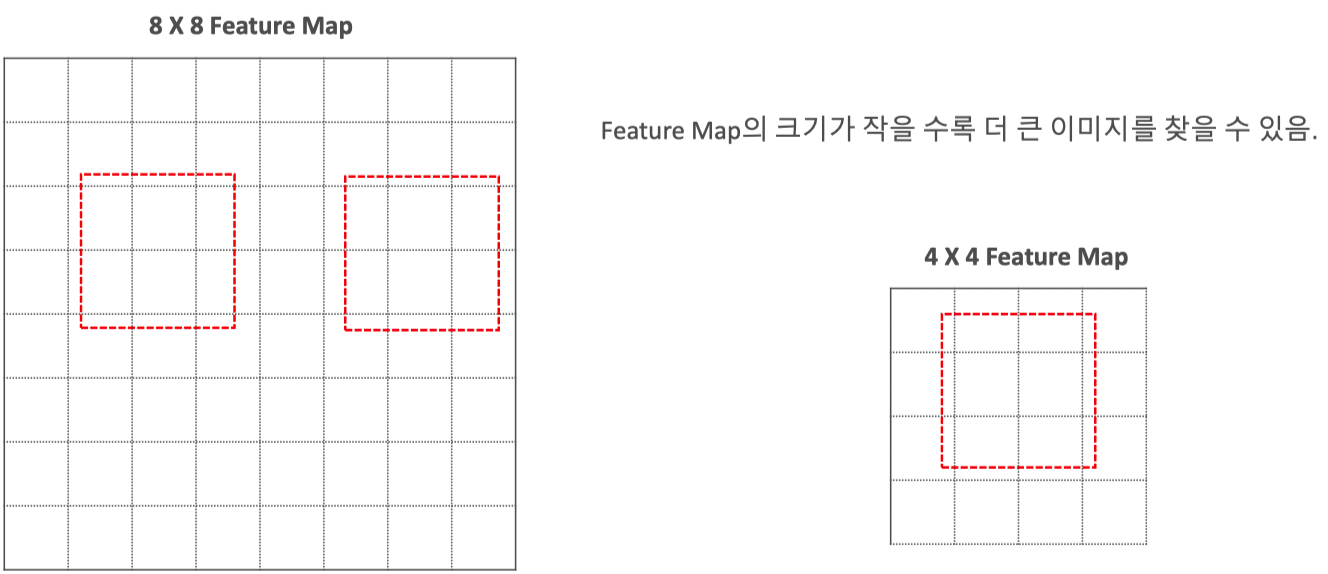
문제점) 좌측 Slide Window에서는 주인공(Big Object)가 잡히지않는다.

이미지 크기가 작아지면 Slideing Window에 Detecting 가능

하지만, SSD에서는 이미지 축소가 아닌 FeatureMap이 축소(추상화) 진행 따라 Slideing Window수행(=이미지 피라미드 과정)

이미지 피라미드 과정

Feature Map기반의 Multi-Scale Feautre Layer

Anchor Box 기반의 Object Detection 모델 – Faster RCNN

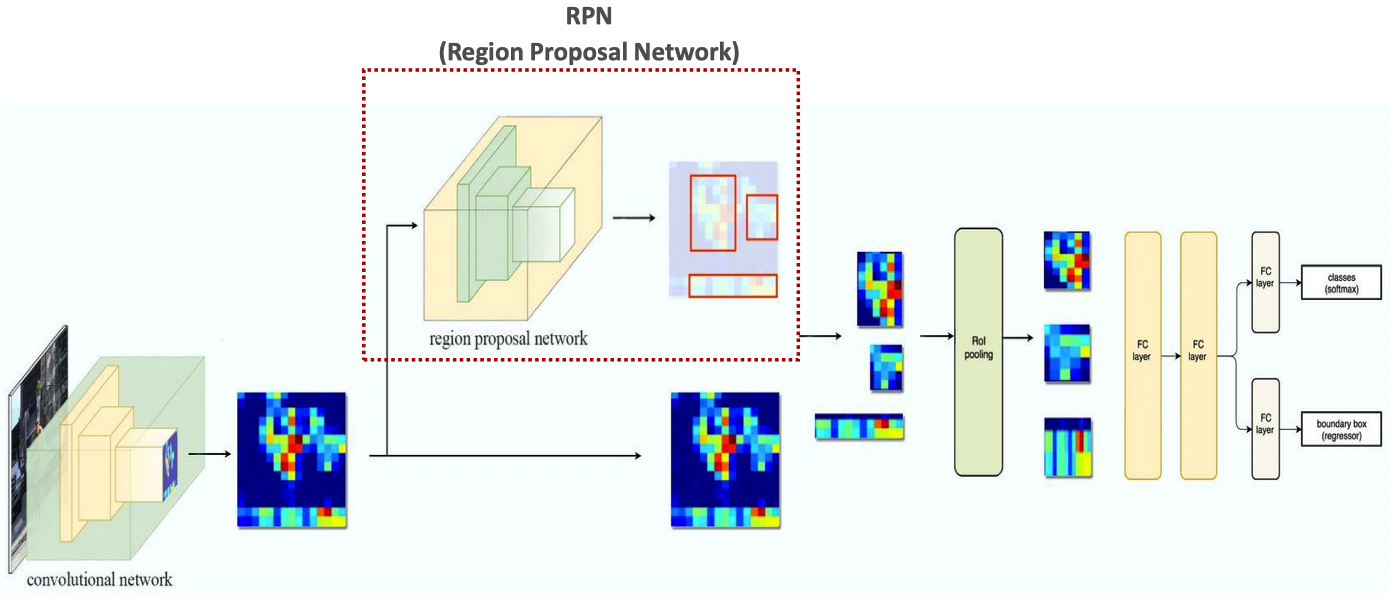
RPN에서의 Anchor Box의 활용

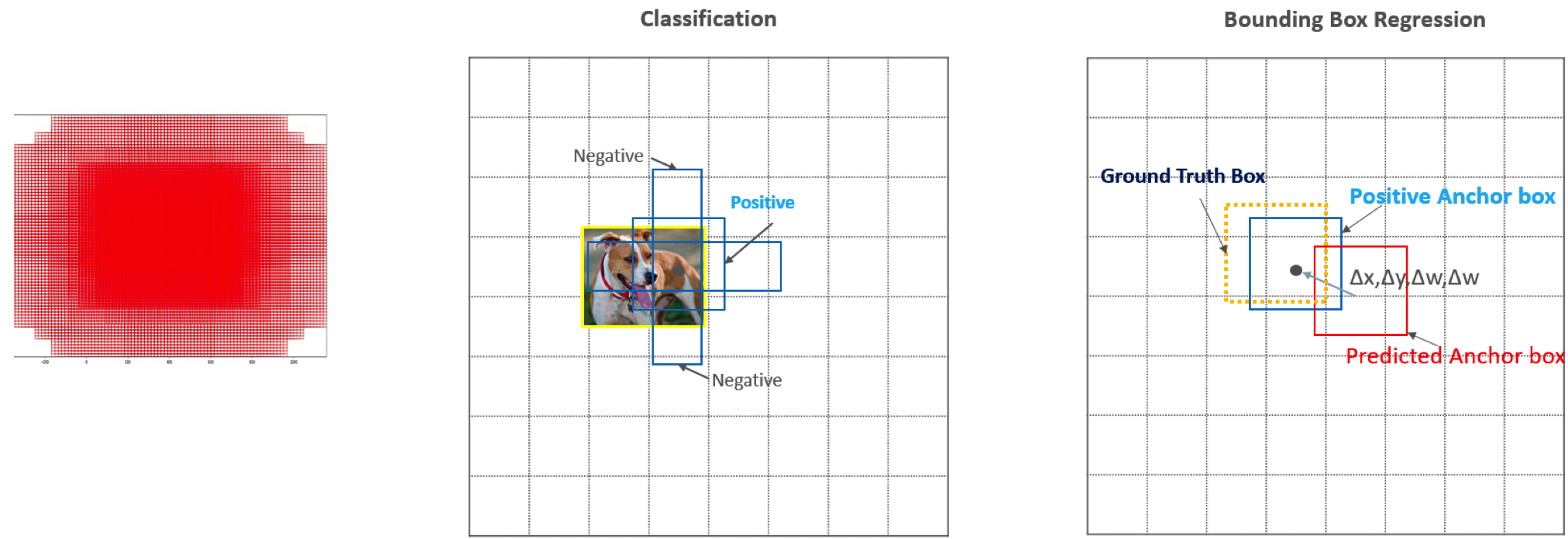
Anchor box 를 활용한 Object Detection

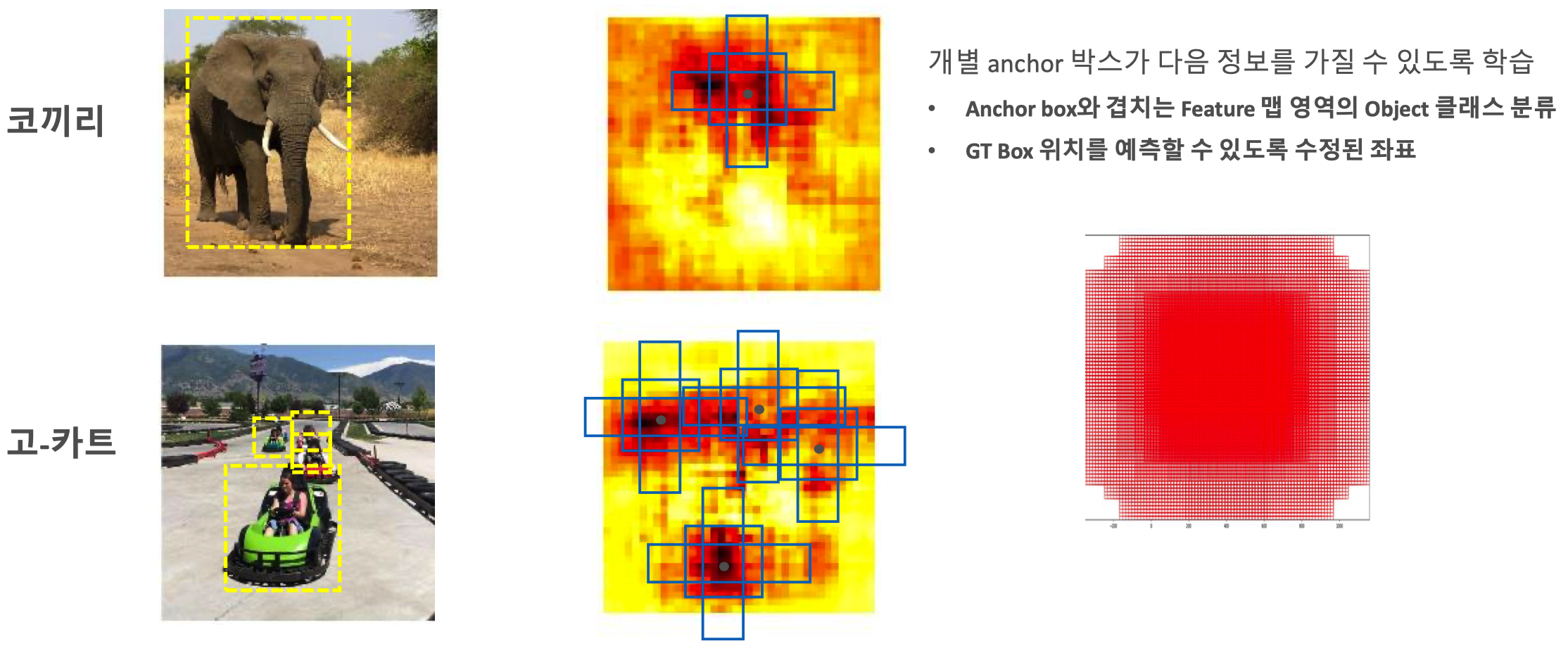
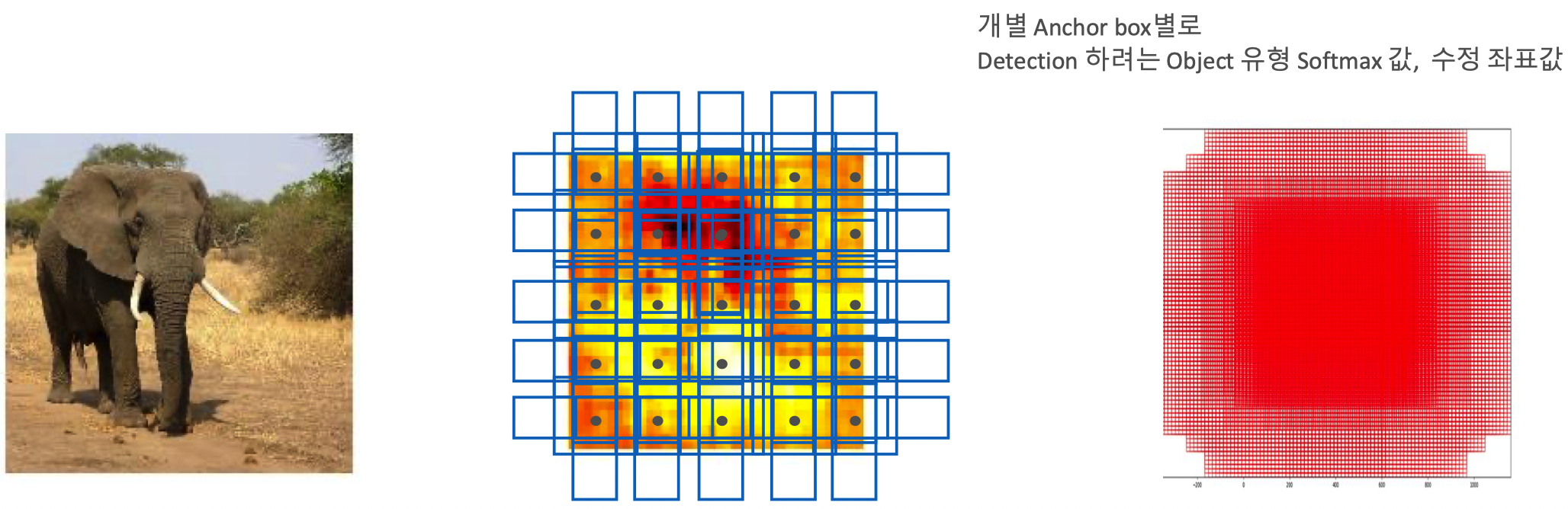
SSD Network 구성

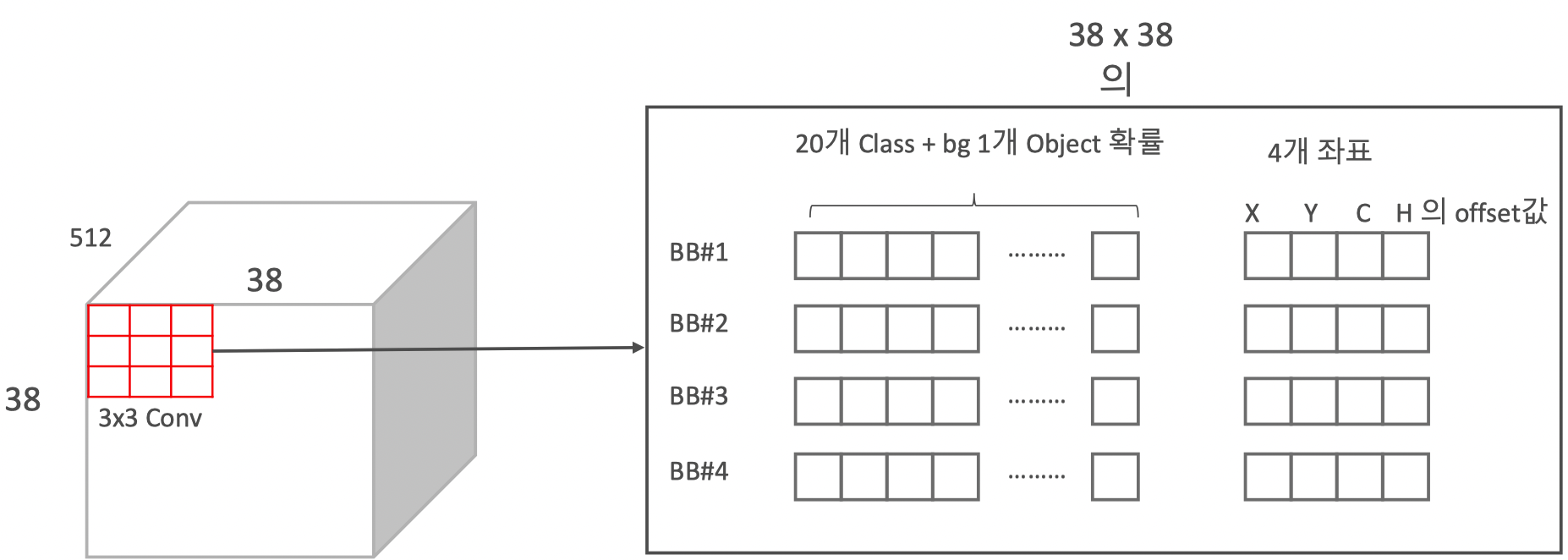
Anchor 박스를 활용한 Convolution Predictors for detection

Loss Function

$L_(x, c, l, g)=1/N(L_{\text {con f }}(x, c)$ + $aL_{\text {loc }}(x, l, g))$

• $L_(x, c, l, g)$ $=>$ $N$은 Matched된 Default box 개수
• $L_{\text {con f }}(x, c)$ $=>$ Classification
• $aL_{\text {loc }}(x, l, g))$ $=>$ Boundig Box regression

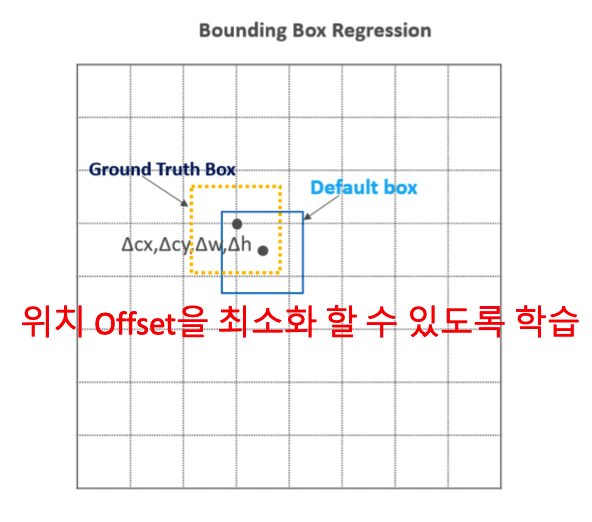
Localization Loss Function

$L_{\text {loc }}(x, l, g)=\sum_{i \in P_{os}}^{N} \sum_{m \in\{c x, c y, w, h\}} x_{i j}^{k} \operatorname{smooth}_{\mathrm{L} 1}\left(l_{i}^{m}-\hat{g}_{j}^{m}\right)$

• $\hat{g}_{j}^{c x}=\left(g_{j}^{c x}-d_{i}^{c x}\right) / d_{i}^{w}$

• $\quad \hat{g}_{j}^{c y}=\left(g_{j}^{c y}-d_{i}^{c y}\right) / d_{i}^{h}$

• $\hat{g}_{j}^{w}=\log \left(\frac{g_{j}^{w}}{d_{i}^{w}}\right)$

• $\quad \hat{g}_{j}^{h}=\log \left(\frac{g_{j}^{h}}{d_{i}^{h}}\right)$

Localization

• Loss Function는 예측된 박스 $l$과 Ground truth box gg 파라미터 사이의 Smooth L1 loss

• 예측해야 할 예측된 상자의 $l^m_i(cx, cy, w, h)$값들은 특이한 $\hat g$값을 예측

• 이때 $\hat g$의 $cx, cy$는 Default box의 $cx,cy,w,h$로 normalize

• 이미 IoU가 0.5 이상된 부분에서만 고려하기 때문에 상대적으로 크지 않은 값들을 예측해야 하고, 비교적 빠르게 수렴할 것으로 예상

• 초기 값 및 $\hat g$의 w, h 은 Default box에서 시작하고

• 예측된 $l$값들은 box를 표현할 때마다 default box의 offset 정보가 필요)

Confidence Loss Function

$L_{\text {conf }}(x, c)=-\sum_{i \in P_{o s}}^{N} x_{i j}^{p} \log \left(\hat{c}_{i}^{p}\right)-\sum_{i \in N e g} \log \left(\hat{c}_{i}^{0}\right) \quad$

$\quad \hat{c}_{i}^{p}=\frac{\exp \left(c_{i}^{p}\right)}{\sum_{p} \exp \left(c_{i}^{p}\right)}$

• Confidence Loss Function는 매칭된(Positive) class에 대해서는 softmax
• 매칭되지 않은(Negative) class를 예측하는 값은 $\hat c_i^0$이고 배경이면 1, 아니면 0의 값
• 최종 predicted class score는 예측할 class + 배경 class를 나타내는 지표

Matching 전략

Bounding box와 겹치는 IOU가 0.5 이상인 Default(Anchor) Box 들의 Classification과 Boudning box Regression을 최적화 학습 수행.

Data Augmentation

• GT Object와 IOU가 0.1, 0.3, 0.5, 0.7, 0.9가 될 수 있도록 특정 Object들의 Image를 잘라냄
• 잘라낸 이미지를 random 하게 sampling
• 잘라낸 sample 이미지는 0.1 ~ 1사이로, aspect ratio는 1/2 ~ 2 사이로 크기를 맞춤
• 개별 sample 이미지를 다시 300x300 으로 고정. 그리고 그중 50%는 horizontal flip

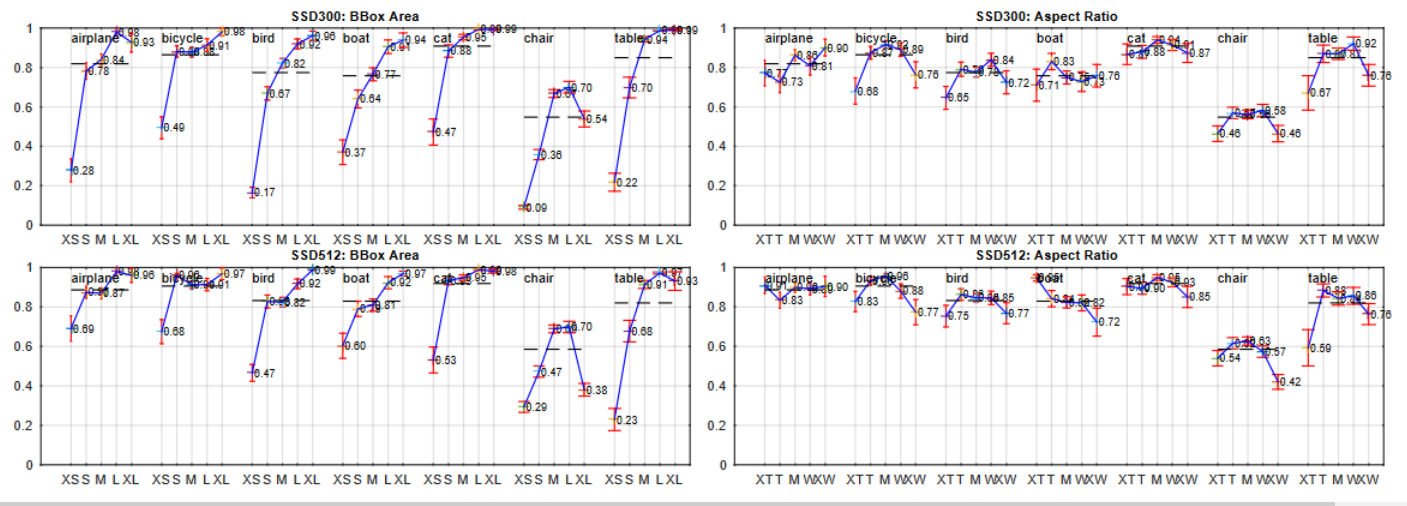
Data Augmentation 후 작은 Object의 Detection 성능 향상

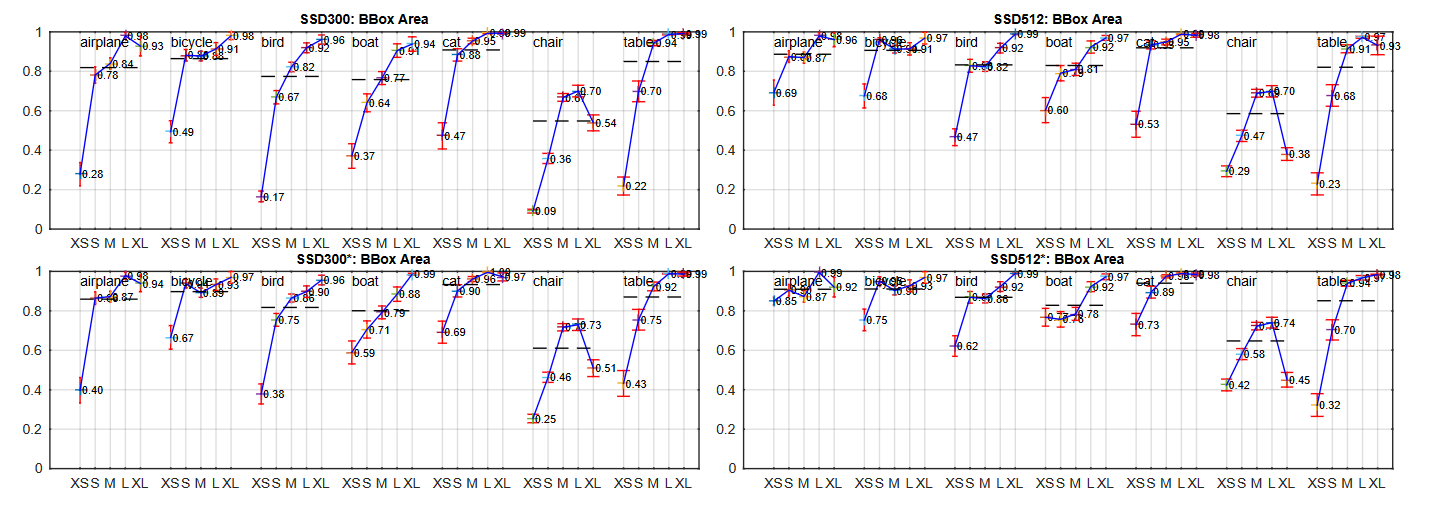
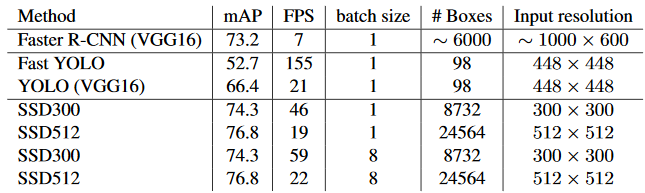
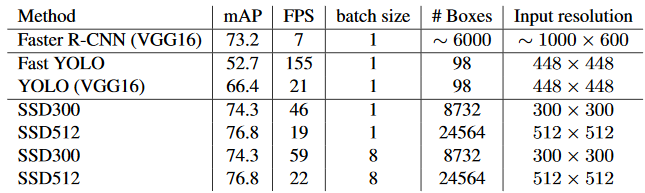
SSD Detection 성능 및 수행 시간 비교

2016년 11월 논문 출시(https://arxiv.org/pdf/1512.02325.pdf)

SSD 성능 비교

SSD 수행 시간 비교

SSD : Single Shot MultiBox Detector

---

SSD는 YOLO v1에서 grid를 사용해서 생기는 단점을 해결할 수 있는 아래와 같은 몇 가지 테크닉을 제안

• Image Pyramid
• Pre-defined Anchor Box

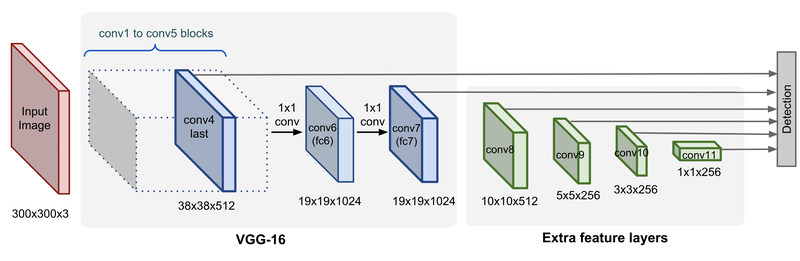
Image Pyramid는 ImageNet으로 사전학습된 VGG16을 사용
VGG에서 pooling layer를 거친 block은 하나의 image feature로 사용 가능

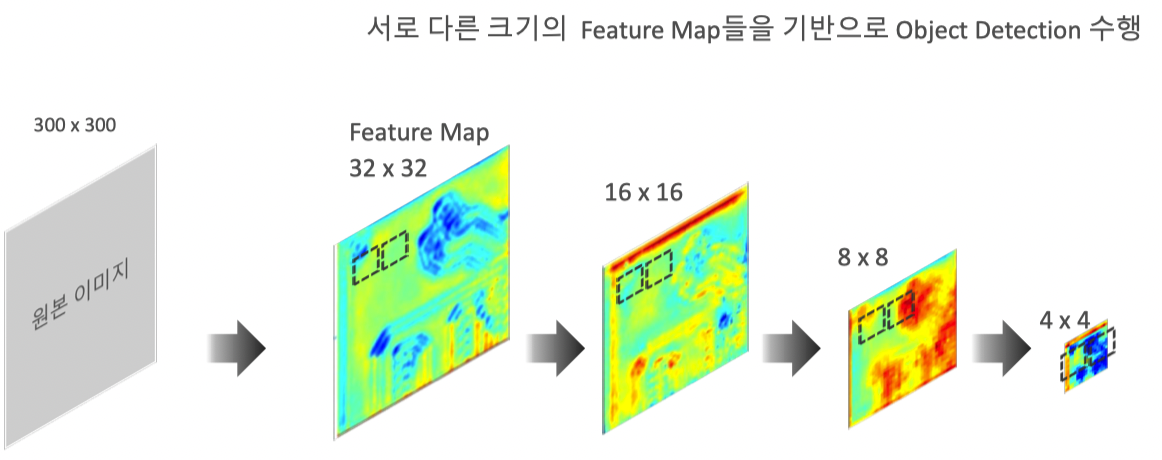
YOLO에서 7x7 크기의 feature map 하나만을 사용했다면,
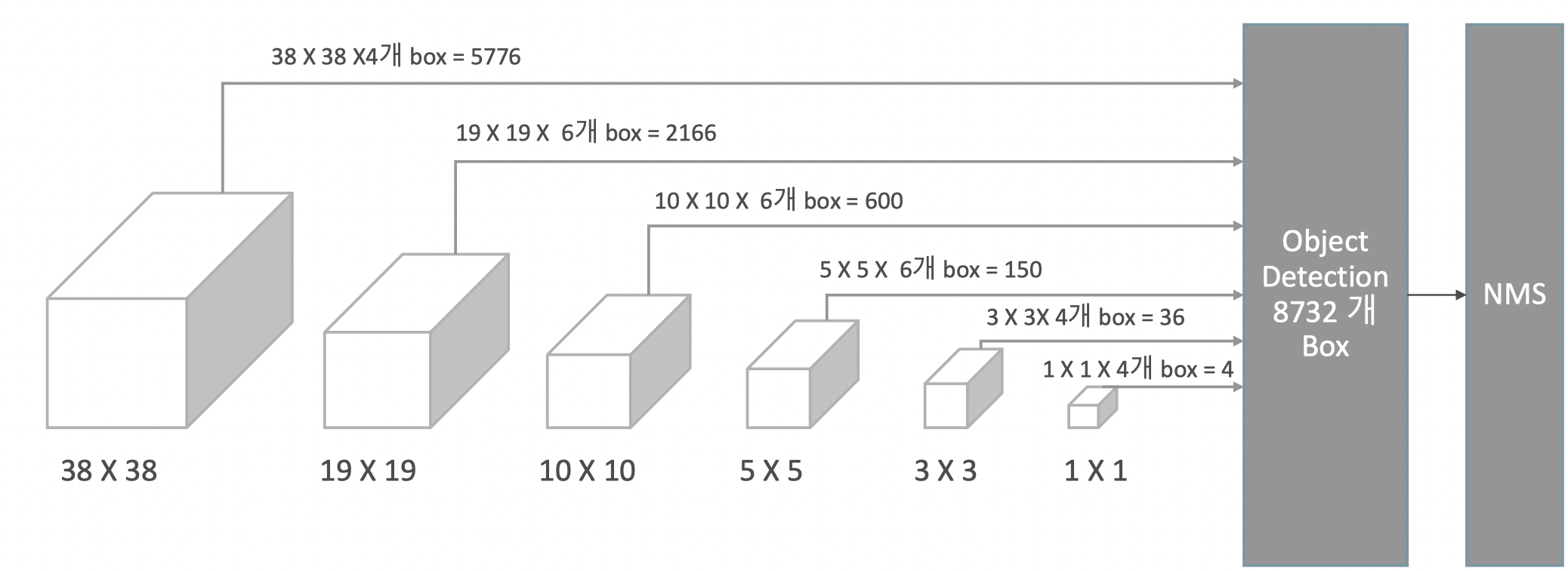
SSD는 38x38, 19x19, 10x10, 5x5, 3x3 등의 다양한 크기의 feature map을 사용
각 feature map은 YOLO의 관점에서 보면 원본 이미지에서 grid 크기를 다르게 하는 효과
따라서 5 x 5 크기의 feature map에서 grid가 너무 커서 small object를 못찾는 문제를 38 x 38 크기의 feature map에서 찾을 수 있는 단서를 마련

Q. Image feature pyramid의 단점?

YOLO와 비교하였을 때 최소 feature map의 개수만큼 계산량이 많다. 38 x 38 크기의 feature map은 box를 계산하기에는 충분히 깊지 않은 network

---

YOLO v1의 두번째 단점은 box 정보 (x, y, w, h)를 예측하기 위한 seed 정보가 없기 때문에 넓은 bbox 분포를 모두 학습할 수 없었다는 점(이로 인한 성능 손실)
따라서 Faster R-CNN 등 에서 사용하는 anchor를 적용할 필요

만약 개가 등장하는 Bounding box가 존재한다면, 그 bounding box만의 x, y, w, h 특성이 존재하기 때문에 pre-defined된 box의 x, y, w, h를 refinement하는 layer를 추가하는 것이 이득이었습니다. 이 anchor box를 SSD에서는 Default box라고 부릅니다.

SSD의 Multi Scale Feature Map과 Anchor Box 적용

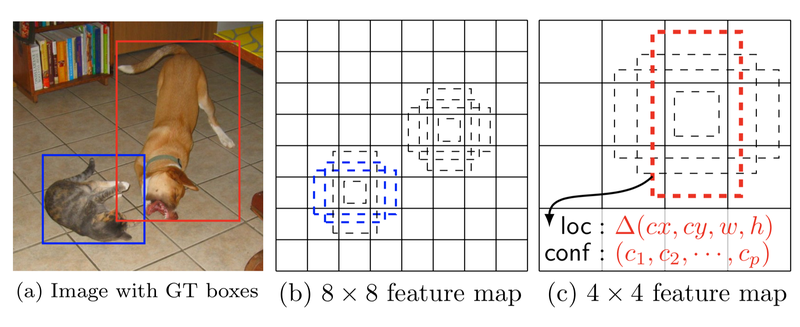
(a)는 이미지 원본파일 GT(Ground Truth) 데이터셋
(b)는 VGG Backbone에 가까운 Fine-Grained feature map 즉, 8x8 grid에서 각각의 grid에 3개 anchor box를 적용
고양이는 크기가 작기 때문에 (a)의 고양이는 8x8 feature map의 grid 중 1개의 anchor box로부터 학습
(c)에서 개의 경우 크고 세로로 긴 경향을 보이기 때문에 receptive field가 넓은 4x4 feature map에서 Detection

Object의 크기 차이로 인해서 각각(고양이 & 개)는 다른 FeatureMap에서 Detaction된다.

Fine Grained란?
"결이 거친, 조잡한"의 뜻을 가진 Coarse-grained와 반대되는 개념으로, 세밀하다는 뜻을 가지고 있습니다. 참고로 fine grained classification은 세밀하게 분류하는 것으로, 상대적으로 비슷한 특징을 가진 class를 분류하는 것입니다.

Default box를 위한 scale

---

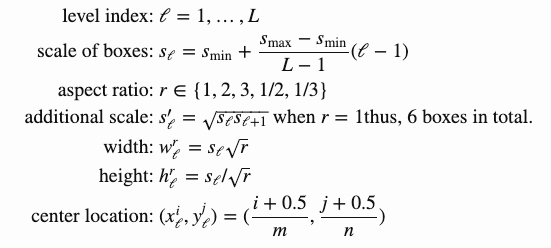
$S_{min}$을 0.2, $S_{max}$를 0.9라고 하고, 위의 식에 넣으면 FeatureMap당 서로 다른 6개의 s값(scale값)
여기서 aspect retio를 {1,2,3,1/2,1/3}로 설정
Default box를 width는 $s_i x$ $\sqrt[]{r}$

• r=1 인 경우 $s_i$ = $\sqrt[]{s_i * s_{l+1}}$

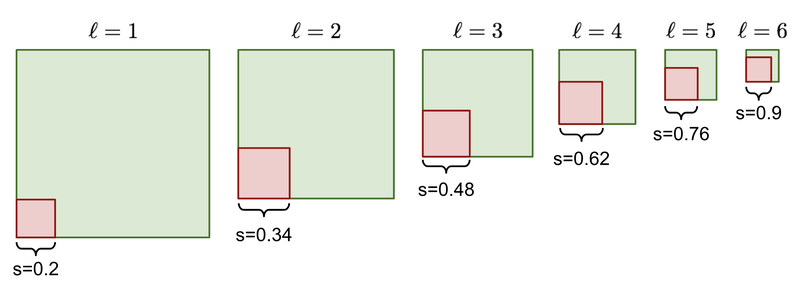
Default box의 cx, cy는 $l$번째 feature map의 크기를 나눠 사용
대략 예측되는 상자가 정사각형이나 가로로 조금 길쭉한 상자, 세로로 조금 길쭉한 상자이기 때문에 2:3으로 임의로 정해도 학습

특이한 경우
가로 방향의 작은 오브젝트는 위의 비율로 정하면 threshold를 0.5로 했을 때 미학습
따라서 학습할 이미지에 따라서 aspect ration를 조정필요
임의로 정하는 것은 비효율적이므로 KNN과 같은 알고리즘을 활용하면 좋은 결과

SSD Loss function

• Objective Loss Function
• Localization Loss Function
• Confidence Loss Function

Objective Loss Function

Localization Loss(loc)와 Confidence Loss(conf)의 가중합(weighted sum)

$L(x, c, l, g) = \frac {1}{N} (L_{con f} (x, c) + \alpha L_{loc} (x, l, g))$

Localization Loss Function

예측된 박스 $l$과 Ground truth box $g$ 파라미터 사이의 Smooth L1 loss

$L_{\text {loc }}(x, l, g)=\sum_{i \in P_{os}}^{N} \sum_{m \in\{c x, c y, w, h\}} x_{i j}^{k} \operatorname{smooth}_{\mathrm{L} 1}\left(l_{i}^{m}-\hat{g}_{j}^{m}\right)$

• $\hat{g}_{j}^{c x}=\left(g_{j}^{c x}-d_{i}^{c x}\right) / d_{i}^{w}$

• $\quad \hat{g}_{j}^{c y}=\left(g_{j}^{c y}-d_{i}^{c y}\right) / d_{i}^{h}$

• $\hat{g}_{j}^{w}=\log \left(\frac{g_{j}^{w}}{d_{i}^{w}}\right)$

• $\quad \hat{g}_{j}^{h}=\log \left(\frac{g_{j}^{h}}{d_{i}^{h}}\right)$

Confidence Loss Function

여러 class의 confidence c의 softmax loss

$L_{\text {conf }}(x, c)=-\sum_{i \in P_{o s}}^{N} x_{i j}^{p} \log \left(\hat{c}_{i}^{p}\right)-\sum_{i \in N e g} \log \left(\hat{c}_{i}^{0}\right) \quad$

$\quad \hat{c}_{i}^{p}=\frac{\exp \left(c_{i}^{p}\right)}{\sum_{p} \exp \left(c_{i}^{p}\right)}$

우선 위의 식 용어를 정리

Category $p$에 대한 $i$번째 Default box와 $j$번째 Ground Truth box의 물체 인식 지표
(0.5 이상이면 1, 미만이면 0으로 정의)

• $N$ : 매치된 Default box의 개수, NN이 0이면 loss는 0입니다.
• $l$ : 예측된 상자(Predicted box)
• $g$ : Ground Truth box
• $d$ : Default bounding box
• $cx,cy$ : Default bounding box의 x, y 좌표
• $w,h$ : Default bounding box의 width, height
• $\alpha$ : 교차 검증으로 얻어진 값 ($α=1$)

---

Hard negative mining

대부분의 Default box가 배경이기 때문에 $x^p_{ij}$이 0인 경우가 다수
따라서 마지막 class의 loss 부분에서는 positive:negative 비율을 1:3으로 정해 출력(즉 high confidence 순으로 정렬해 상위만 유의미)

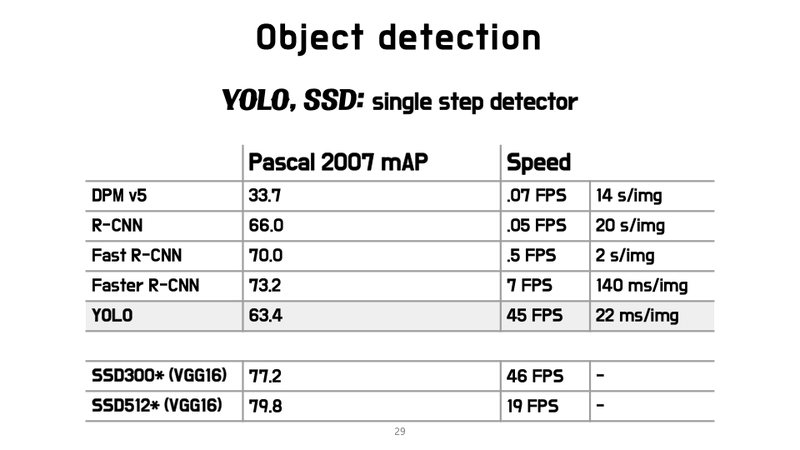
SSD 성능 비교

SSD 수행 시간 비교