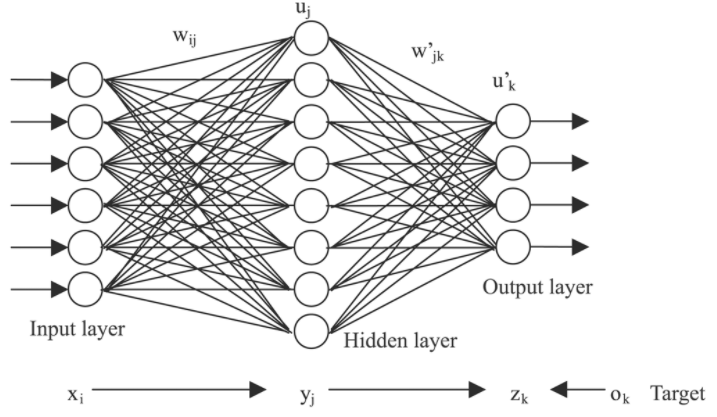
합성곱 신경망의 발견

CNN을 설명하고 이 신경망이 컴퓨터 비전 작업이라면 어디에서난 사용되는 이유를 알아보자

다차원 데이터를 위한 신경망

CNN은 초기 신경망의 단점을 해결하기 위해 도입됐다. 여기에서는 이 이슈를 해결하고 CNN이 이 문제를 어떻게 다루는지 설명한다.

완전 연결 네트워크(FCN)의 문제점

이미지를 처리할 때 완전 연결 네트워크가 갖는 두가지 주요 단점은 다음과 같다.

• 매개변수의 폭발적인 증가
• 공간 추론의 부족

각 항목에 대해 알아보자

매개변수의 폭발적인 증가

이미지는 엄청난 개수의 숫자로 구성된 복합적인 구조다(즉 이미지 높이 x 이미지 너비 x 이미지 깊이 혹은 채널 개수). 크기가 작은 단일 채널 이미지(28x28 크기의 작은 이미지라도 784개의 입력 벡터를 갖고 있음)라도 이미지마다 위와 같은 개수의 값으로 이루어진 크기의 입력 벡터를 갖고 있으므로 이를 완전 연결 네트워크에 입력할 경우 첫 번째 계층에서 이미 (784,64)형상의 가중치 행렬를 갖는다. 이는 이 변수만을 위해 최적화해야 할 매개변수 값이 784 x 64 = 50176개나 된다는 의미다.

RGB 이미지가 커지거나 네트워크가 깊어질수록 이 매개변수는 급격히 증가한다.

공간 추론의 부족

이 네트워크의 뉴런이 어떤 구분 없이 이전 계층의 모든 값으 받기 때문에('뉴런이 모두 연결돼 있다') 이 신경망은 '거리/공간성'이 없다. 데이터의 공간 관계를 잃기 때문이다. 이미지 같은 다차원 데이터는 밀집 계층에 칼럼 벡터로 전달될 수 있기 때문에 그 연산은 데이터 차원이나 입력값의 위치를 고려하지 않는다. 더 정확하게는 모든 픽셀 값이 계층별로 '원래 위치와 관계없이' 결합되므로 픽셀 사이의 근접성 개념이 완전 연결(FC, fully-connected) 계층에서 손실된다.

직관적으로 보면 일부 입력값이 동일한 픽셀 또는 동일한 이미지 영역에 속한다는 등의 공간 정보를 고려할 수 있다면 신경망 계층은 훨씬 더 똑똑해질 것이다.

CNN도입

CNN은 앞에서 언급한 단점을 해결할 수 있는 간단한 해결책을 제공한다. CNN은 전방 전달(forward), 역전파(backpropagation) 등의 방식으로 작동하지만 아키텍처를 약간 영리하게 변경했다.

무엇보다도 CNN은 다차원 데이터를 처리할 수 있다. 이미지의 경우 CNN은 '3차원 데이터(높이x너비x깊이)'를 입력으로 취하고 뉴런을 그와 비슷한 볼륨으로 정렬한다.

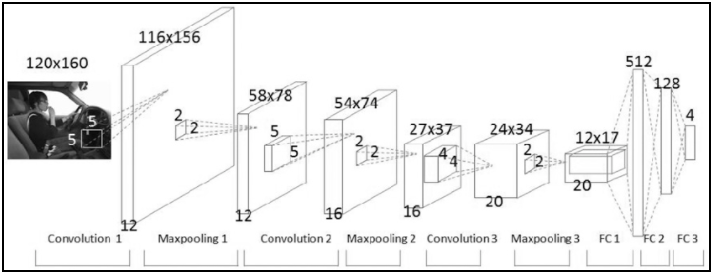
이것이 CNN이 참신한 두 번째 이유다. 뉴런이 이전 계층의 모든 요소에 연결된 완전 연결 네트워크와 달리 CNN의 각 뉴런은 이전 계층에서 이웃한 영역에 속한 일부 요소에만 접근한다. 이 영역(일반적으로 정사각형이며 모든 채널에 걸쳐 있다)을 뉴런의 수용 영역(또는 필터 크기)이라고 한다.

뉴런을 이전 계층의 이웃한 뉴런과만 연결함으로써 CNN은 훈련시킬 매개변수 개수를 급격히 줄일 뿐 아니라 이미지 특징의 위치 정보를 보존한다.

CNN 작업

이 아키텍처 패러다임으로 몇 가지 새로운 유형의 계층도 도입해 다차원성과 지역적 연결성을 효율적으로 활용한다.

합성곱 계층

CNN이라는 이름은 그 아키텍처의 핵심에 해당하는 합성곱 계층에서 비롯됐다. 이 계층에서는 동일한 출력 채널에 연결된 모든 뉴런이 똑 같은 가중치와 편향값을 공유함으로써 매개변수의 개수를 더 줄일 수 있다.

개념

가중치와 편향값을 공유하는 특정 뉴런은 공간적으로 제한된 연결성을 통해 전체 입력 행렬에서 슬라이딩하는 단일 뉴런으로 생각할 수도 있다. 각 단계에서 이 뉴런은 현재 슬라이딩하고 있는 입력 볼륨(HxWxD)의 일부 영역에만 공간적으로 연결된다. 필터 크기가 (k_H, k_W)인 뉴런에 대해 이 제한된 입력 차원(k_H x k_W x D)이 주어지면 이 뉴런은 합계에 활성화 함수를 적용하기 전에 입력 값을 선형으로 결합한다. 수학적으로 (i, j) 위치에서 시작한 입력 패치에 대한 뉴런의 응답 z는 다음과 같이 표현할 수 있다.

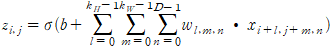
여기에서 뉴런의 가중치는 w, 편향값은 b이며 시그마는 활성화 함수(예를들어 시그모이드)다. 뉴런이 입력 데이터를 받을 수 있는 각 위치에 대해 이 연산을 반복함으로써 차원이 H x W인(여기에서 H, W는 뉴런이 입력 텐서를 각각 수직 및 수평으로 슬라이딩할 수 있는 횟수를 말한다) 완전한 응답 행렬 z를 얻는다.

합성곱 계층에는 여전히 N개의 다른 뉴런 집합(즉 같은 매개변수를 공유하는 N개의 뉴런 집합)이 있으므로 그에 대한 응답 맵이 함께 쌓여서 형상이 H x W x N인 출력 텐서가 된다.

완전 연결 계층에서 행렬 곱셈을 적용한 것과 동일한 방식으로 여기에서 합성곱 연산을 사용해 모든 응답 맵을 한 번에 계산할 수 있다. 이 연산에 익숙한 사람이라면 '입력 행렬에서 필터를 움직인다'는 설명을 듣자 마자 이 연산을 떠올렸을 것이다. 반면에 이 연산에 익숙하지 않은 사람이라면 합성곱의 결과가 필터 w를 입력 행렬 x에서 움직이면서 현재 위치에서 시작하는 x의 패치와 필터 사이에 내적을 계산해 합성곱의 결과를 얻을 수 있다고 이해하면 된다. 이 연산을 아래 그림에서 확인할 수 있다.

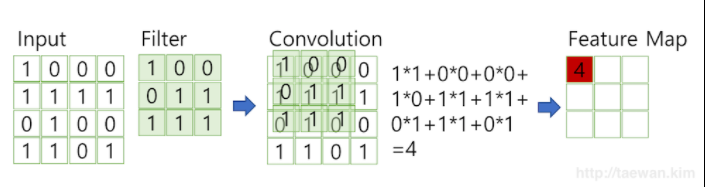
속성

N개의 다양한 뉴런의 집합을 갖는 합성곱 계층은 형상이 D x K x K(필터가 정삭가형인 경우)인 N개의 가중치 행렬(필터 또는 커널이라고도 함)과 N개의 편향값으로 정의도니다. 따라서 이 계층에서 훈련시킬 값은 N x (Dk^2+1)개뿐이다. 반면 완전 연결 계층이라면 유사한 입력과 출력 차원을 가질 때 (H x W x D) x (h x w x N)개의 매개변수가 필요하다. 앞서 보여줬듯이, 완전 연결 계층에서 매개변수 개수는 데이터 차원에 영향을 받는 반면 합성곱 계층에서는 데이터 차원이 매개변수 개수에 영향을 주지 않는다.

이 속성 덕분에 합성곱 계층은 두 가지 이유로 컴퓨터 비전 분야에서 실제로 막강한 도구가 된다. 첫 번째 이유는 이전에도 설명했듯이 입력 이미지 크기가 커져도 튜닝해야 할 매개변수 개수에 영향을 주지 않고 네트워크를 훈련시킬 수 있다. 두 번째 이유는 합성곱 계층은 어떤 이미지에도 그 차원 수와 상관없이 적용될 수 있다는 점이다. 완전 연결 계층을 가진 네트워크와 달리 순수 합성곱 네트워크에서는 입력 크기가 다양하더라도 별도의 조정이나 재 훈련 과정을 거칠 필요가 없다.