Data Exploration and its Objectives
주어진 데이터 셋의 특성, 관계를 파악하는 것은 문제 해결에 중요한 부분이다.
Data Exploration의 목적은 데이터의 특징 파악인데 분포, 이상값, 특성의 수, 특성 간의 관계 유무 등을 파악한다.
Data Sets and Attributes
테이블 형태의 데이터 셋을 구조화된 데이터 셋(Structured Data Set)이라고 한다.
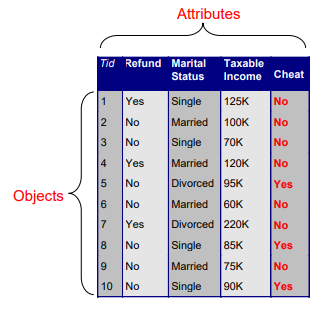
- Data Object :
- Attribute : 각 Data Object마다 가지고 있는 속성.
- attribute의 수가 크면 Data의 Dimensionality가 크다고하고, Object가 많으면 Sample의 수가 크다고 말한다.
Types of Data Attributes
- Nominal/Ordinal/Integer/Ratio attributes
- Discrete/Continuous attributes
- Symmetric/Asymmetric attributes
Nominal/Ordinal/Integer/Ratio attributes
attributes를 구분하는 방법은 4가지 연산 중 어떤 것을 적용해야 유용한가로 나뉜다.
1. Distictness :
2. Order :
3. Addition :
4. Multiplication:
- Nominal : 1. ex)ID, 눈 색깔, 우편 번호
- Ordinal : 1,2 ex) 점수, 키
- Interval : 1,2,3 ex) 날짜, 온도
- Ratio : 1,2,3,4 ex) 길이, 나이, 개수
Nominal과 Ordinal은 일반적으로 카테고리 값을 가지는 속성이다. 카테고리 간의 순서를 매길 수 있으면 Ordinal, 매길 수 없으면 Nominal 속성으로 볼 수 있다. Interval과 Ratio는 보통 Numeric 값을 가지는 속성이다. Interval 속성과 Ratio 속성의 차이는 Ratio 속성에서 0은 존재하지 않음을 뜻하지만 Interval 속성에서는 그렇지 않다. 예를들어 길이가 0인 것이나 개수가 0이면 없는 것이다.
Discrete/Continuous attributes
말 그대로 유한한 값을 가지면 Discrete, 연속적인 값을 가지면 Continuous이다.
Symmetric/Asymmetric attributes
- Asymmetric attributes : 0이 아닌 값만 중요하게 고려되는 속성 ex) 학생들이 공통적으로 수강하는 과목(학생들이 같이 듣지 않는 과목에 대해서는 중요하게 보지 않음)
- Symmetric attributes : 0인 값도 0이 아닌 값과 같이 중요하게 여기는 속성. Asymmetric과 반대.
Types of Data Exploration
- Descriptive statistics : 속성의 평균, 범위, 편차 등의 정보를 파악
- Visualization techniques : 데이터를 시각화해 상관관계, 분포를 파악
Descriptive statistics : Univariate Exploration
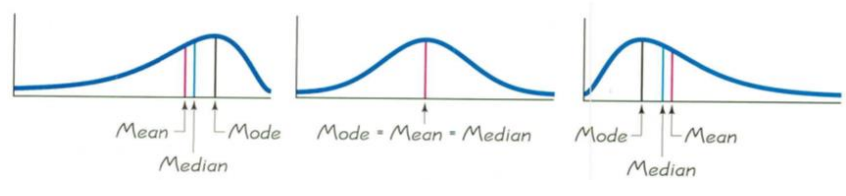
하나의 속성에 대해 데이터 분석. 해당 속성의 평균, 중앙값, 최빈값, 범위, 표준편차 등을 조사한다.
-
mean : 산술적인 평균. 이상치에 민감
-
median : 데이터를 정렬하였을 때의 중앙값. 이상치에 민감하지 않다
-
mode : 가장 많이 나타나는 값.
위 세개의 속성을 알아보면 데이터의 분포를 추정할 수 있다.
-
Range : 데이터의 최소값에서 최대값까지의 범위.
-
Standard deviation : 평균으로부터 데이터들이 얼마나 떨어져 분포하는 지를 나타내는 지표. 표준화를 하므로 Range보다 분포를 파악하기에 좋다.
-
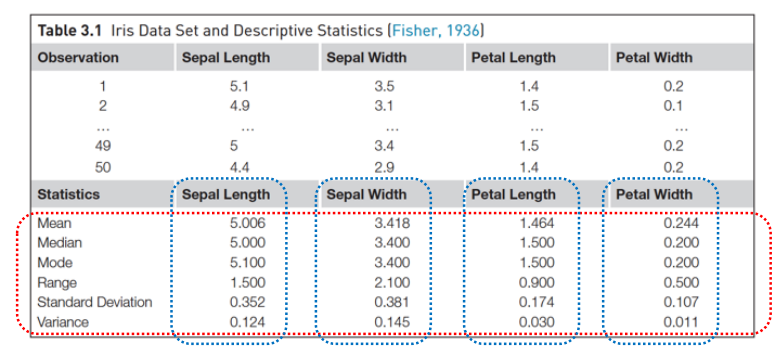
특정 클래스의 속성 분석(iris setosa species)
-
전체 클래스의 속성 분석
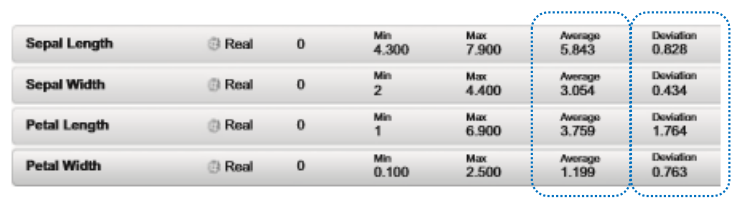
-
해석 : 특정 클래스의 속성에서는 표준 편차가 작았던 Petal Length 속성이 전체 데이터에 대해서는 편차가 크다. 이는
Descriptive statistics : Multivariate Exploration
동시에 하나 이상의 속성에 관해서 분석. 속성간의 관계를 파악하는 것이 목적이다.
- Correlation : Pearson correlation coefficient(r)로 측정하는데, 피어슨 상관 계수는 속성 간의 선형 관계를 표현한다.
의 범위를 가지며 r의 절댓값이 1에 가까울수록 두 속성이 선형적으로 상관성이 크고, 0에 가까우면 서로 상관성이 없다고 해석할 수 있다. - 한계 : 속성들이 평균, 분산, 상관계수가 모두 같아도 분포가 매우 다를 수 있다. 상관계수 r은 선형 관계만 보일 수 있고 비선형적인 관계에 대해서는 나타내지 못한다.
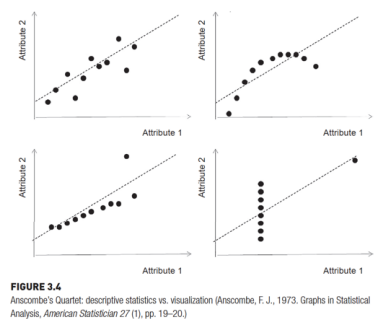
Data Visualization
데이터를 그래프와 같이 시각화하여 분석하는 방법
- Univariate visualization: 하나의 속성에 대해 조사
- Multi-variate visualization: 동시에 여러개의 속성에 대해 조사
- Visualizing high-dimensional data in parallel axes : 많은 속성에 대해 조사
Univariate Visualization - Histogram
단일 속성의 데이터 분포를 대략적으로 파악하기 위한 도구
Numeric Data가 있을 때 bin value에 따라 막대 개수를 다르게 하여 분포를 대략적으로 혹은 자세하게 볼 수 있다.
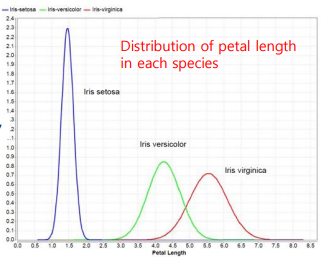
아래처럼 히스토그램을 클래스 별로 구분하여 보았을 때 유용하게 정보를 얻을 수도 있다.
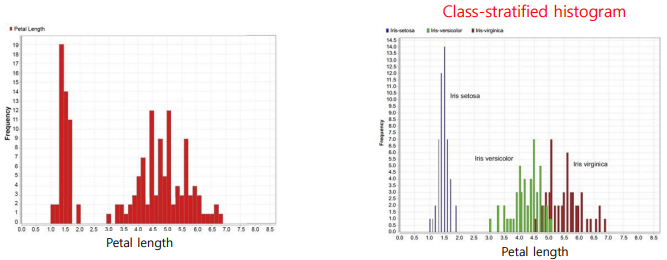
Univariate Visualization - Box plot
속성의 주요 정보인 중앙값, 사분위수, 이상값 등을 파악하기 위한 도구
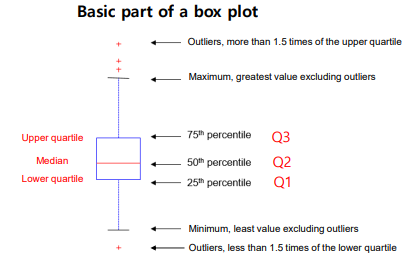
평균, 표준 편차를 보여주는 경우도 있고 여러 속성에 대해 나타내어 속성들의 정보를 빠르게 파악하거나 동일 속성을 클래스 별로 나누어 그려서 분포 특성을 볼 수 있다.
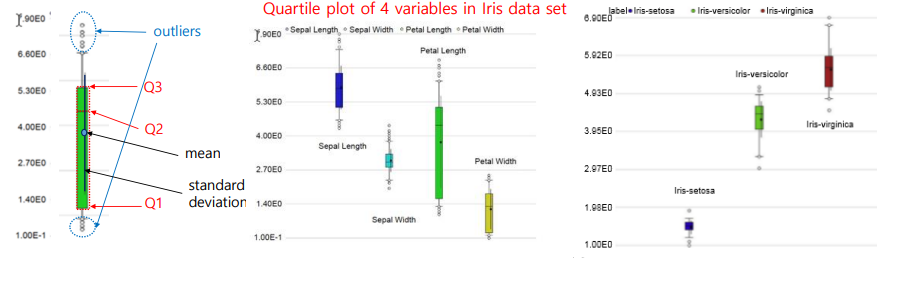
Univariate Visualization - Distribution plot
Continuous Numeric 값을 가지는 속성에 대해 분석하는 도구
히스토그램과 비슷한 시각을 제공하지만 연속된 값에 대한 분포를 보여준다.