summary
- Unet 구조에 Attention gate (AG)를 적용하여 의료 데이터 Segmentation에 좋은 성능을 제시한 논문
- skip-connection에 AG를 적용
- Latent vector를 Query로 skip connection을 key로 Attention을 사용한 방법으로, self-attention의 성질을 활용하였음
- 1x1x1 channel wise convolution
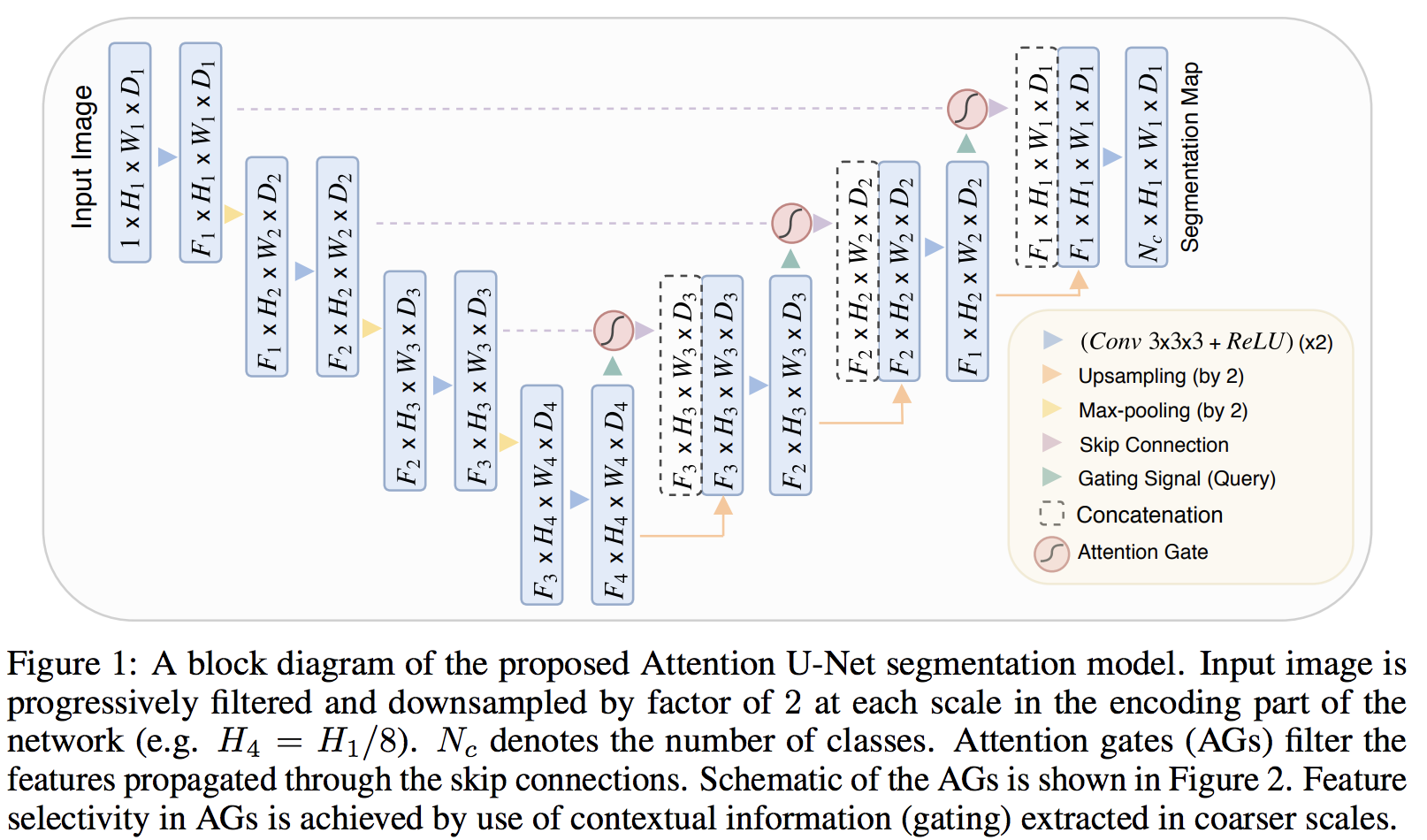
Structure
전체적인 구조는 위의 그림과 같다. Unet구조에서 Encoder에서 Decoder로 skip connection을 진행 할 때, Attention Gate라는 부분이 생겼다. AG가 어떻게 동작하는지를 중점적으로 살펴보자.
Attention Gate (AG)
우선 본 논문에서는 의료 영상분석에서 새로운 self-attention gating module을 소개한다고 하는데, self attention이 무엇일까?
Attention is all you need제시한 Self-attention의 개념은 Q,K,V가 같은 vector로 출발하였기에 self라는 개념을 붙였다. (seq2seq에서의 attention은 K,V가 encoder의 hidden state matrix, Q가 Decoder의 hidden state이다)
- self-attention의 Q,K,V 같은 vector 를 사용하여 연산한다.
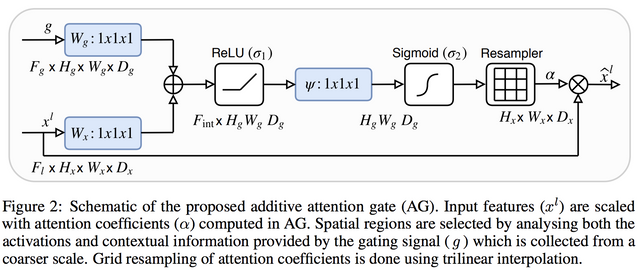
그렇다면 왜 Attention Unet의 AG가 Self-attention인가? 전체적인 구조와 밑의 그림을 보면
: gating signal(그 전 layer의 latent vector이다)
: skip connection이다.
생각해보면, gating signal 는 의 연산(Conv-> maxpool-> UpConv)으로부터 온 것이고, 다시 을 사용하여 attention을 구하므로 self-attention의 관점으로 볼 수 있다.
- 다른 논문에서는 2개의 vector를 연결하여 한개의 vector로 만들어 연산하는 과정을 vector concatenation-based attention이라고 정의한다.
위의 그림을 수식으로 표현해보자.
notation을 먼저 정리를 해보자면 ,
: Relu
: sigmoid
: Convolution output with activation function
: batch size
: Linear leanable parameter
bias term
: Symbol of learnable parameter
where : filter(channel) dimension 즉, image의 width, height등에 대해서 연산한 것이 아니라 filter에 대해서 연산을 진행한 것을 명심해야한다.
- (1)부터 확인해보면,skip connection으로 부터 온 과 gating signal(Latent vector)를 각각 dot product (attention Score를 구함)를 진행한 다음, Learnable parameter 에 대해서 dot product를 진행한다(attention value의 개념)
이때 이다. 즉, 모든 Sample에 대해서 각각 다른 Attention value를 가지게 되고 ,AG연산은 Filter에 대해서 진행하였으므로, 가 된다. 즉, Image한장에 대하여 Pixel별로 attention value가 존재한다는 것
이를 두고 논문에서는 channel-wise Convolution이라고 명칭한다.- (2)는 (1)에 sigmoid를 씌워 0~1로 만들어 준 값 과 skip-connection 을 elementwise연산을 진행한다.
즉,
※ 가 sigmoid의 output이므로, 는 attention으로 찾아낸 의미있는 값에 더 집중하게 된다
backpropagation
편미분 방정식은 추후에 정리를 해보자
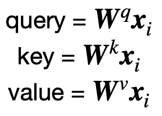
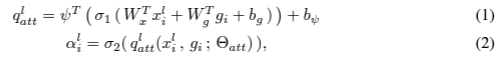
유익한 글 감사합니다 :) 혹시 편미분 방정식에 관한 내용은 정리 중이신가요?