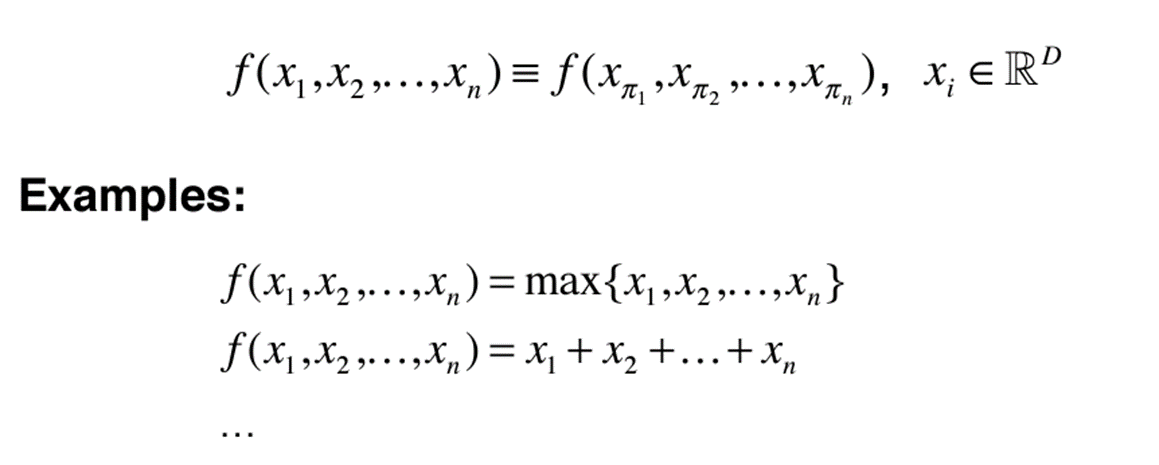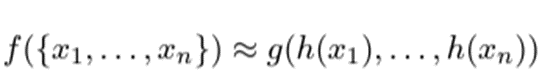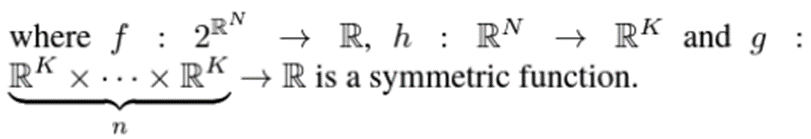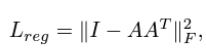논문 구현 및 실험
참고 list
summary
- Point Data를 그대로 학습하는 architecture를 제안함.
- symmetric function을 이용하여 Unordered data에 대해서도 학습이 가능하고, T-net을 사용하여 Data의 geometric information을 학습
- 논문 표현 상 network는 key point의 sparse set으로 부터 요약된 모양을 학습한다고 한다.
key point
- max pooling - aggregate info. from all the points
- local & global information combination structure
- two joint alignment network
prior knowledge
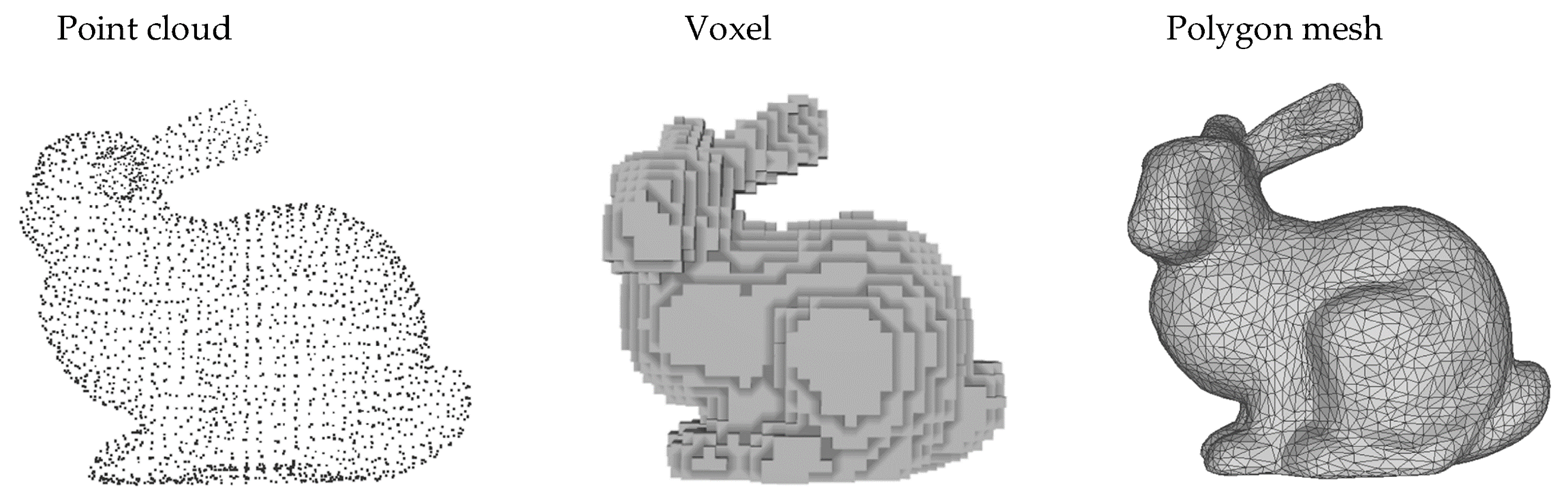
mesh 에 대해서 간략하게 알아야할 필요가 있다. 밑의 그림이 3d를 가장 잘 표현하는 그림인데,
- point cloud란 데이터를 점의 분포를 사용하여 표현한 것
- voxel은 Volume Element의 약어로, 3D공간을 격자 형태로 분할한 작은 3D부피 단위를 의미한다. 3차원 pixel로 생각하면 편함
- Mesh는 polygons을 사용하여 3D data를 표현하는데, vertex와 index, faces로 이루어져 있다.
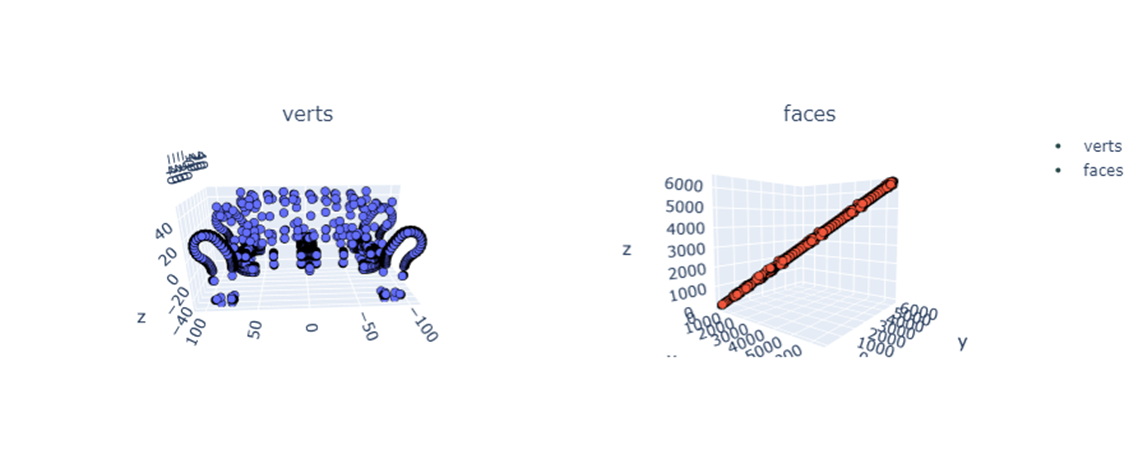
vertex와 faces를 간략하게 살펴보면 point cloud에서 사용하는 modelnet의 경우 vertex와 faces로 이루어져 있다. 이를 살펴보자
vertex는 말 그대로 point의 꼭지점(x,y,z)를 의미하며, faces는
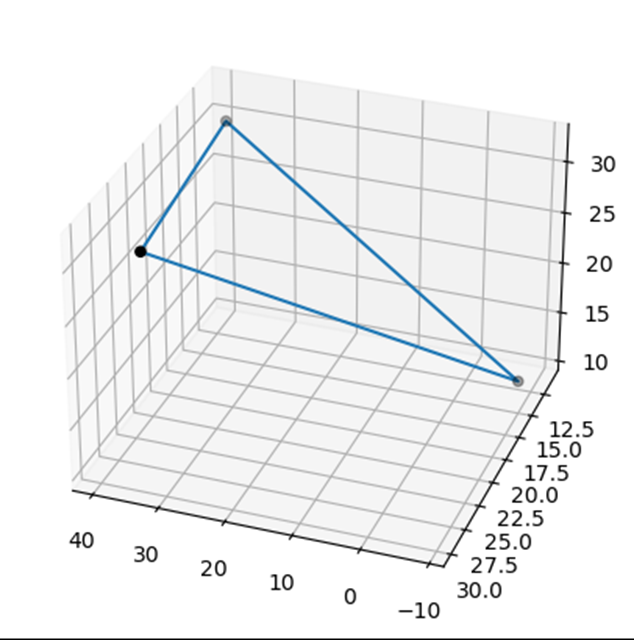
vertex의 집합으로 이루어져 있다. faces를 vertex에 index하면 다음과 같은 3개의 좌표가 나오는데, 이를 이어보면
밑의 그림처럼 삼각형으로 표현할 수 있다. 즉, Model net은 mesh data를 triangle mesh를 사용하여 표현한 것이다.
previous
기존의 방식은 preprocessing을 통해서 point cloud 데이터를 3D-> 2D로 바꾸거나 3D conv등을 사용하여 point cloud를 학습하였음(Image grid or 3D voxels or Kernel optimization for weight sharing)
Limit
- 3D -> 2D는 unnecessarily voluminous한 data가 되었음
- 3D geometry data는 학습하지 못함
- Interection point는 여전히 예측이 잘 안됨
- Pointnet은 transform 없이 Point cloud 그대로를 학습하는 network를 제안
task
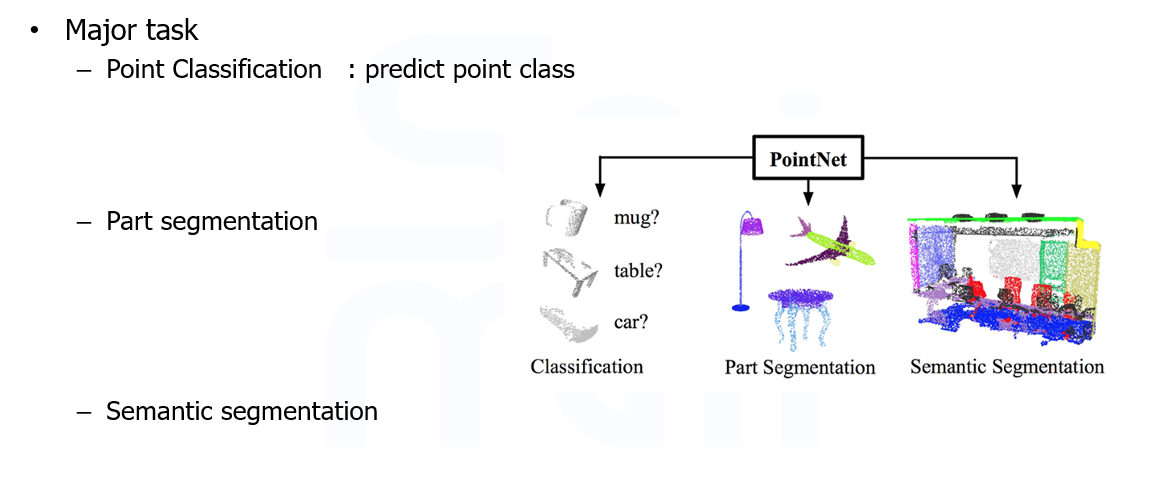
- Point net을 적용할 수 있는 task는 크게 3개
- point Classification: 말 그대로 각 점(point)의 class를 분류한다
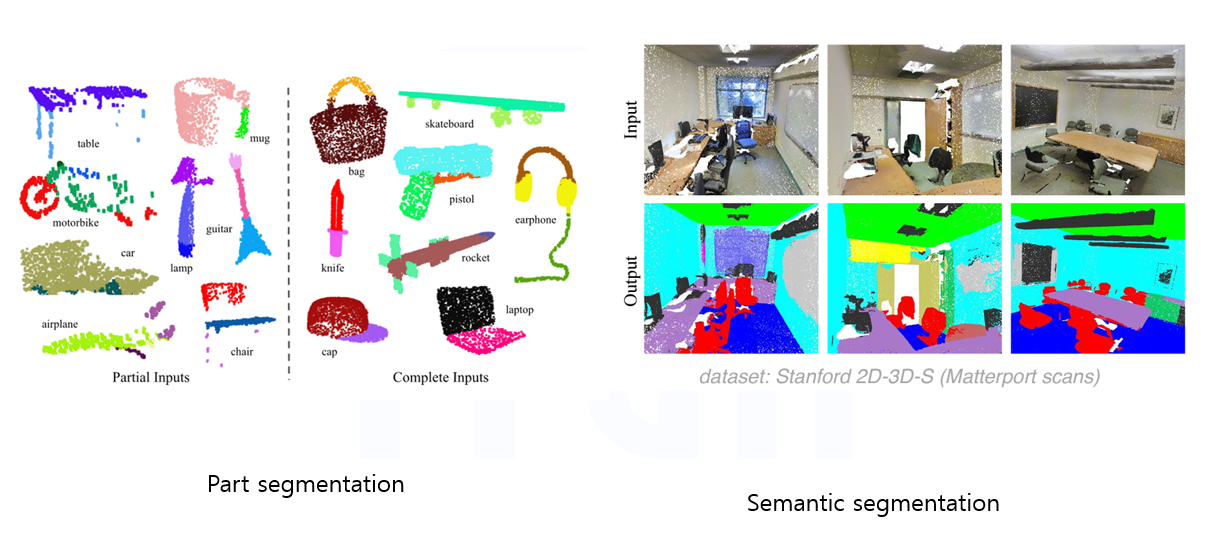
- Part segmentaion : point의 부분을 segmentation 진행한다'
- Semantic segmentation: 객체를 segmentation을 진행한다.
Problem Statement
Point Cloud를 학습하기 위해 Data를 간략히 살펴보면 다음과 같은 수식으로 정의할 수 있다.
3D points:
where : Point num
where
: cordinate in
: cordinate in
: cordinate in
이때 각 point마다 feature vector가 있다고 가정하면 최종적인 Point data의 차원은 다음과 같다 .
output
Point net의 output은 의 차원을 가지는데 ,은 score를 의미한다(softmax를 생각하면 될것)
Properties in Point set
- Unordered
Point들은 Image나 sequence data 처럼 specific order를 가지지 않는다.
- Interaction among points
각각의 point는 distance metric을 가지는데 ,이는 point가 isolated 되어 있지 않고, neighboring point는 subset에 대해서 의미를 가지는 것을 의미한다.(이 개념을 통해서 Graph Neural Network를 적용할 수 있다)
- Invariance under transformations
geometric object로서 point set에 대해서 invariant를 학습할 수 있어야함
특히 Point set은 Permutation 문제가 존재하는데, data가 unordered하기 때문에 입력으로 넣을때 다음 data는 어떤 데이터를 넣어야 하는가 하는 문제가 생긴다.
즉, Point set은 N!의 permutation이 생긴다
Solving Permutation
Permutation을 해결하기 위해서 Pointnet은 Symmetric function을 제안한다
Symmetric function: input의 순서에 상관없이 같은 결과를 output으로 내는 함수(ex: max, sum)
- 논문에서 제시한 Symmetric function은 Max pooling이다!
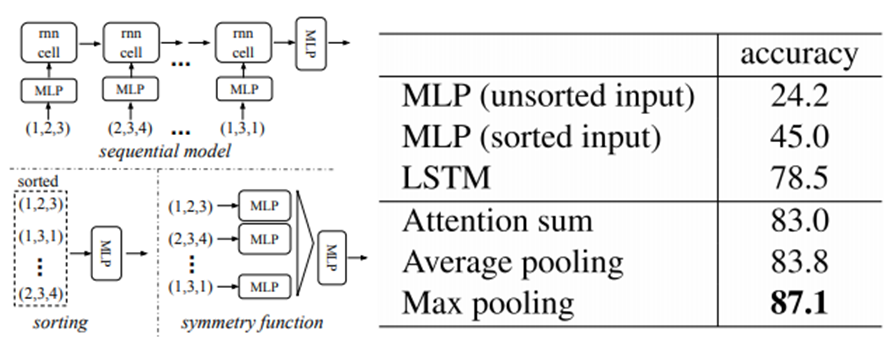
⁕ Permutation을 극복하기 위해서 논문에서는 3개의 실험을 제시하였는데,
1: Point set에 대해서 임의의 기준으로 Sort를 진행
2: Seqeunce를 줘서 RNN을 사용
3: symmetric function을 사용
그 결과는 다음과 같았다고 한다
Model Architecture
논문에서 제시한 model를 살펴보자
수식은 다음과 같이 정의한다
point set(차원이 이유 Power Set의 정의 때문이다. 쉽게 생각해서 {0: set에 속하지 않음,1: set에 속함}을 가정한 가능한 모든 집합의 경우의 수)을 넣었을 때 value값을 나타내는 함수를 라고 할 때 는 에 대한 함수로 근사할 수 있는데,
where : MLP , : symmetric function이다. (수식을 보면 N개의 point를 전부 넣어 값이 값이 하나만 나오게 된다)
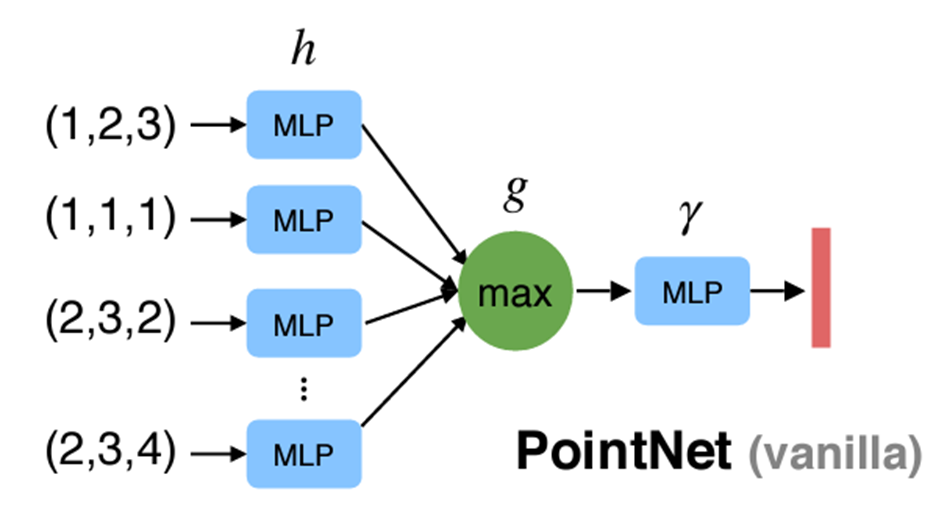
즉, 구조화 하면 다음과 같다
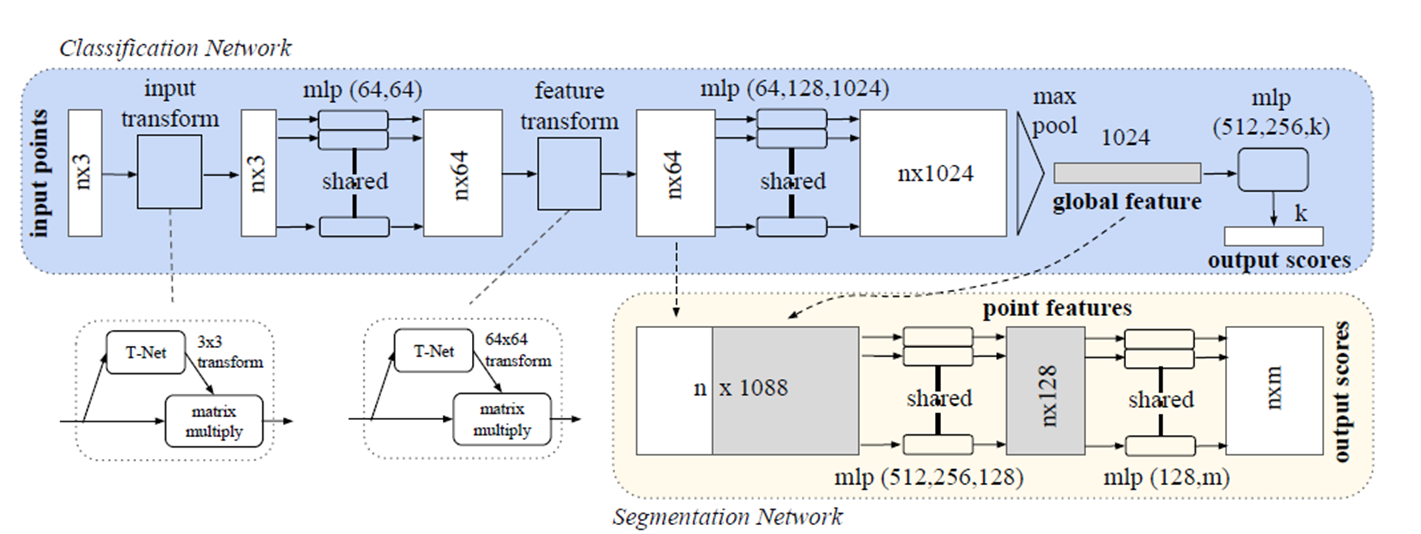
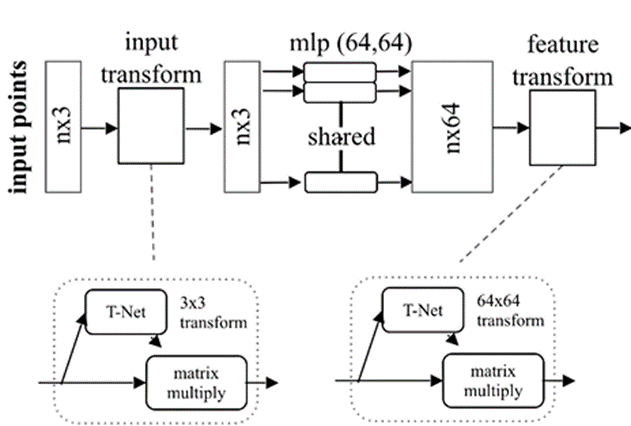
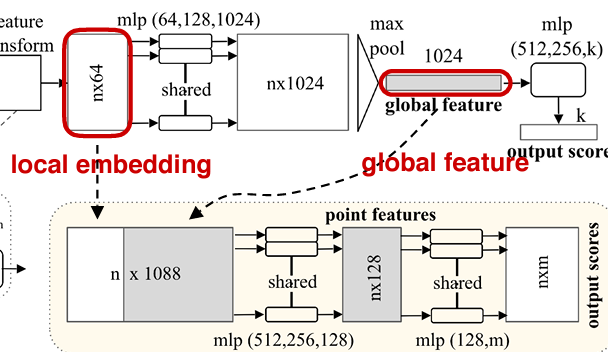
이제 전체 구조를 보면
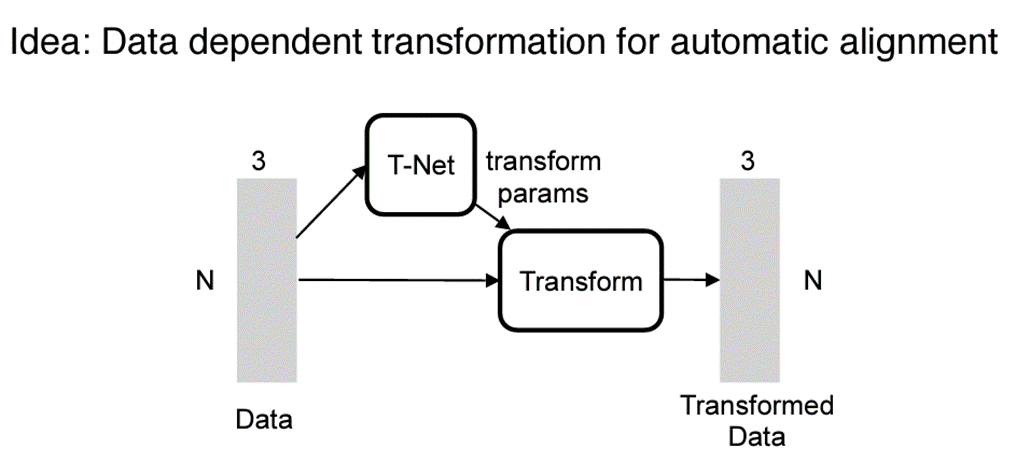
다음 그림과 같은 구조를 따르는데 , 여기서 T-net이라는 구조가 있다. T-net의 주 역활은 Data Dependent를 automatirc하게 학습을 하는것인데 논문에서는 Affine Transformation을 배운다고 한다. 이 T-net이 2부분 존재하는데,
- input transform: Data에 대한 transformation matrix를 학습
- feature transform: MLP를 통해서 extracted된 feature에 대해서 transformation matrix를 학습한다.
(학습한 transformation matrix를 input에 대허서 matmul을 진행( )
where feature alignment matrix
여기서 학습하는 는 Affine transformation을 생각하면 된다. point cloud데이터에 대해서 선형 변환을 통하여 잘 학습될 수 있도록 하게끔 하는 Transformation matrix를 학습하는 과정(Spatial Transformation Network를 참고하면 된다.)
Affine matrix의 경우 다음과 같음
Loss Regularization
input transform을 통해서 학습하는 transformation matrix는 으로 matrix의 크기가 그리 크지 않다.
그러나 featrue transformation matrix는 로 dimmension이 높다. 논문에서는 feature transformation matrix를 orthogonal matrix로 규제하기 위해서 regularization을 준다.
여기서 A는 위에서 정의한 데로 feature alignment matrix이며, 이 되기 위해선 가 되어야한다. 즉, 이 되어야 하며, 이 존재하기 위해선 이고, full rank가 존재해야한다. 즉, 학습을 진행하면서, A가 orthogonal해진다면 의 각 column은 independent하게 될것이며, 에 가까워 진다
- Orthogonal하게 설정하는 이유는 orthogonal의 정의에 의하면 각 column이 basis가 될 수 있고, 이는 정보 손실이 일어나지 않는 방향으로 Linear transformation이 가능하다는 것을 의미하기 때문이다.
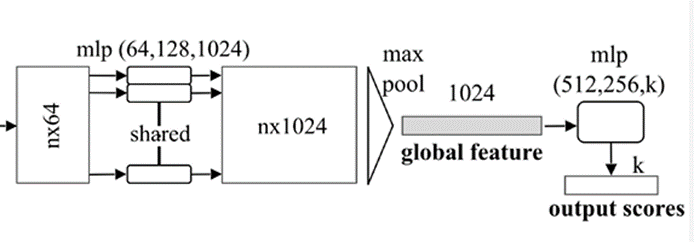
maxpool
학습한 feature를 통해서 maxpool(symmetric function)을 적용한다 적용한 vector는 global feature vector를 사용하여 최종적인 point score를 classification을 진행한다.segmentation
위의 global feature vector를 사용하여 segmentation을 진행한다. local embedding(point net에서 extracted된 feature matrix)부분과 global feature(max pool을 사용해 구해낸 feature matrix)를 사용하여 segmentation의 input으로 사용할 수 있다.
- segmentation에서의 loss는 MIou를 사용한다
result
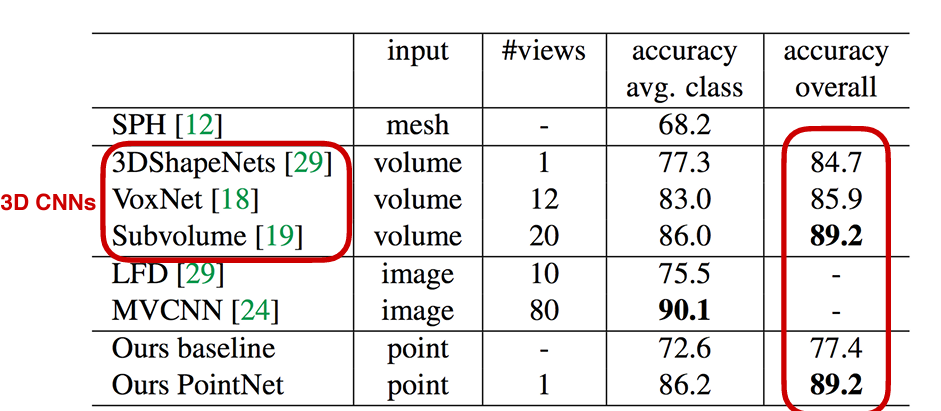
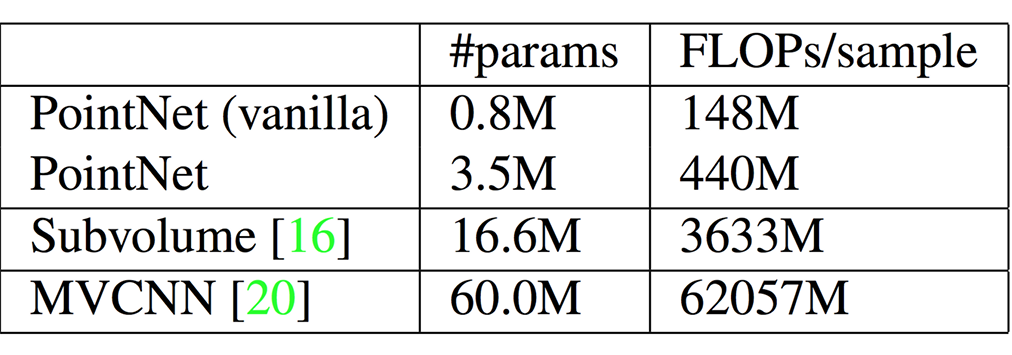
point net은 전체적인 성능과 parameter 모두 기존의 3d cnn에 비해서 좋은 성능을 내었다고 한다.
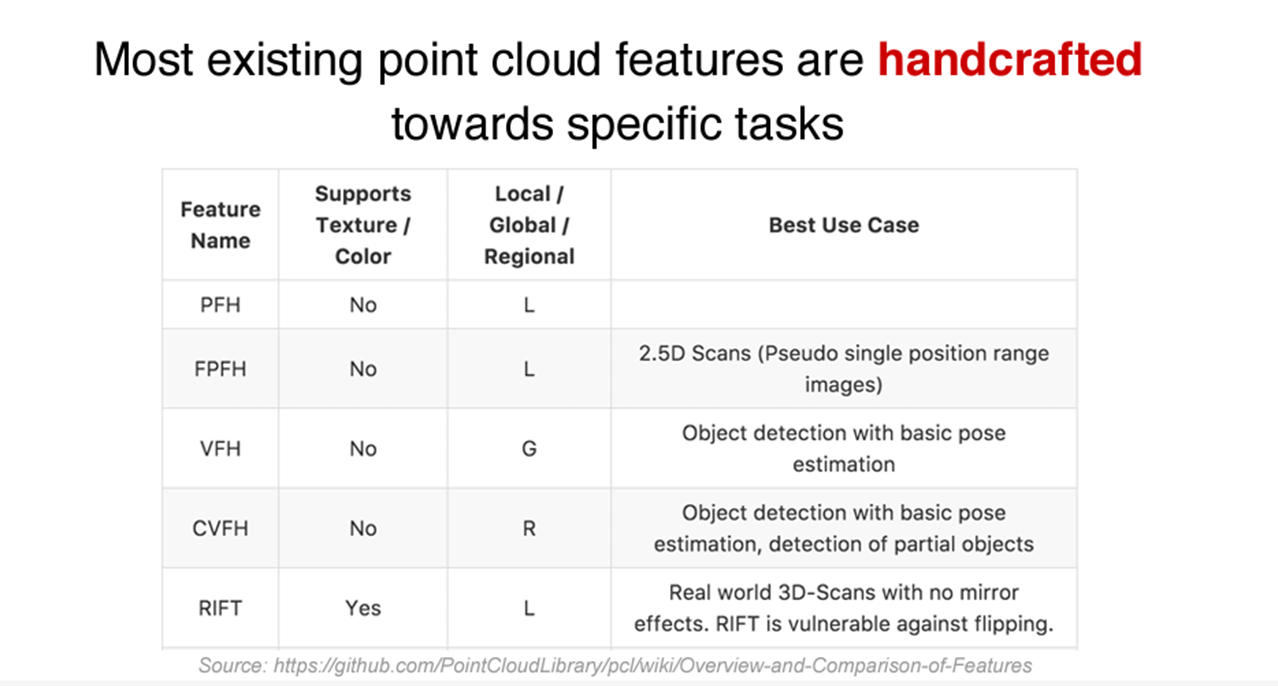
※baseline은 hand-crafted point feature를 사용하여 진행했다고 한다. baseline은 same 9-dim local feature과 3개의 추가적인 것(local point density, local curvature and normal)를 사용하여 Standard MLP를 돌린 모델
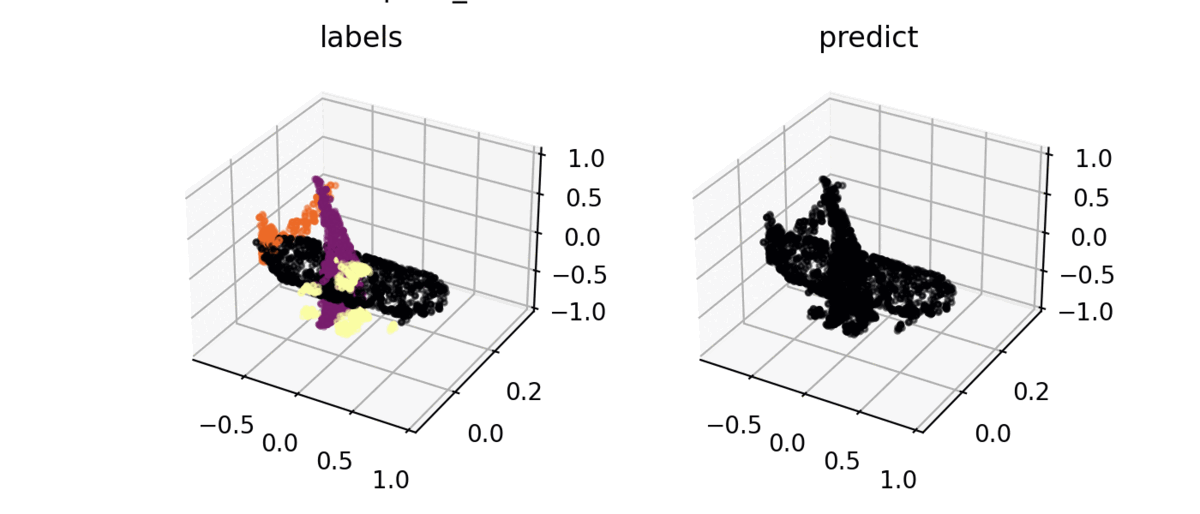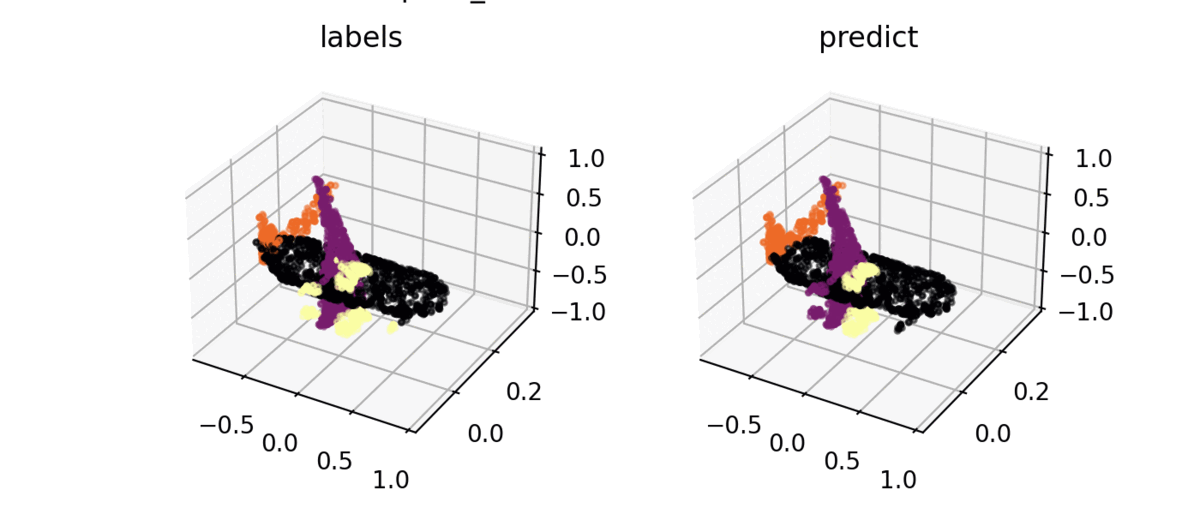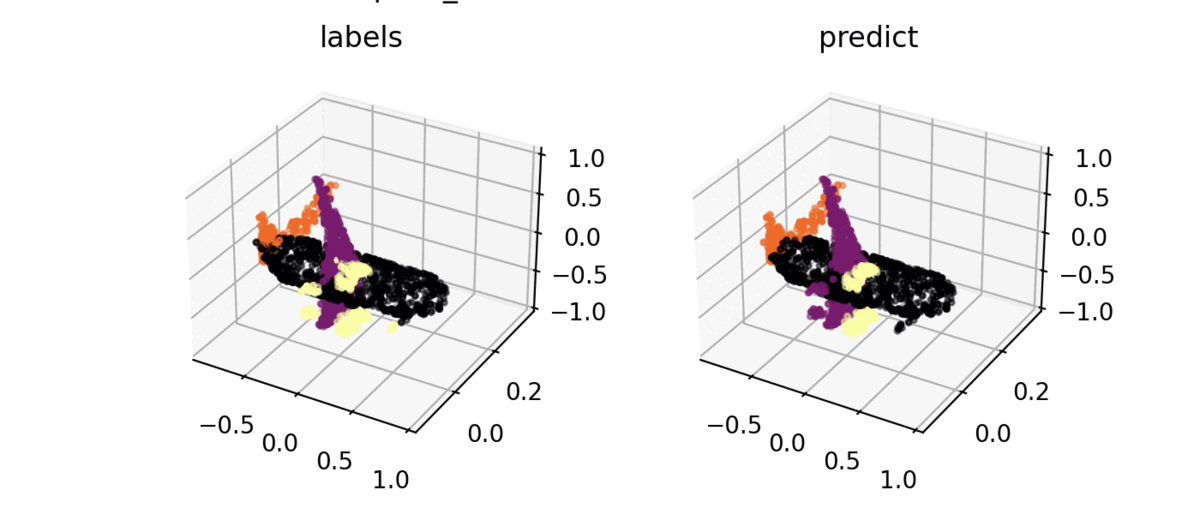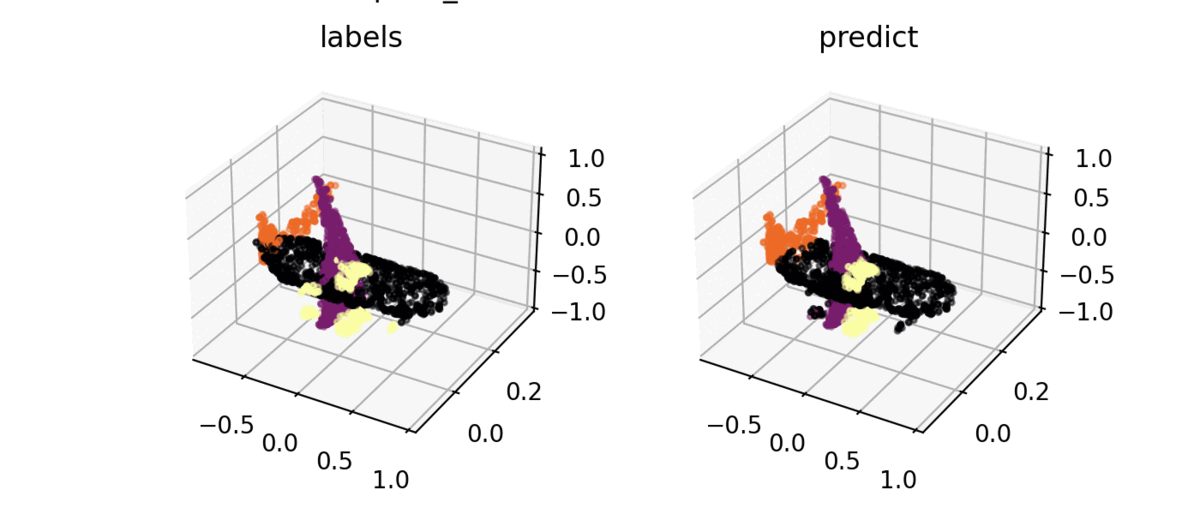
Segmentation result
ShapeNet을 사용하여 구현 결과를 시각화해보면 밑의 그림처럼 잘 분류하는 것을 볼 수 있다.