저자: Ben Mildenhall,
소속: UC Berkeley
학회: ECCV 2020 Best Paper
공식 홈페이지,
참조1:Youtube
참조2:187 blog

summary
- 5d input 을 9 layer- MLP에 넣어서 output으로 rendering 이미지를 합성하는 것 (위의 gif처럼 가상의 3D 장면을 2D이미지로 변환하는 것을 rendering이라고 한다.)
- Positional encoding 을 사용하여 High frequency정보를 주어 고화질 이미지를 생성
- Hierarchical volume sampling을 사용하여 biased distribution을 해결
- 2D image를 사용하여 3D rendering 이미지를 생성한다는 아이디어가 재미있음
절차
- 3D point 생성을 위해서 Camera ray를 사용 (COLMAP등으로 카메라의 3D pose를 추정할 수 있음)
- color, density를 출력하기 위해서 2d가 바라보는 방향의 해당하는 point를 사용(camera ray를 이해해야한다)
- 2D이미지의 color, density를 accumulate 하기 위해서 classical volume rendering 기술을 사용한다.
classical volume rendering은 naturally differentiable하다고 한다. -> sgd를 사용하여 최적화 할 수 있는 이유
prior knowledge
Computer Grapics 내용 및 생소한 개념이 나와서 정리를 하는 것이 좋을 것 같다.
-
signed distance: 특정점 또는 객체와의 거리를 나타낸 값. 일반적으로 최단 거리를 의미한다.
-
Implicit representation: 수학적인 모델링으로 rendering을 진행하는 것을 의미
-
Explicit representation: Polygon mesh를 사용하여 rendering을 진행하는 것을 의미
대부분의 rendering은 explicit representation을 사용한다. polygon mesh는 다각형으로 mesh를 표현하는 것으로, vertex, faces(index)로 구성되어 있음
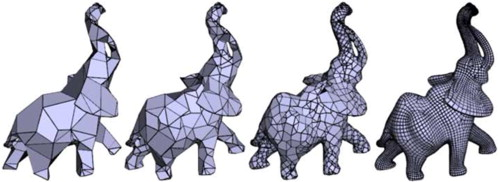
Polygon mesh example: 다각형으로 3D mesh data representation -
Novel view Synthesis

input으로 한 장면(객체)에 대해서 여러장으로 sampling이 된 이미지를 주면 input으로 주지 않은 새로운 view에 대한 image를 생성하는 task를 의미한다. -
Scene Representation
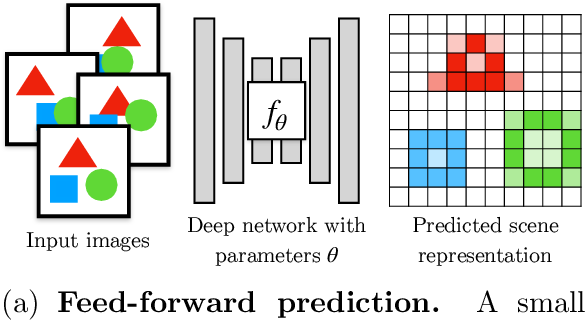
기존은 discreate 한 방법들 (ex, Voxel, Point cloud, Mesh)으로 많이 사용되었는데, input으로 low dimension (e.g. x,y cordinate)를 주었을 때, Voxel, Pixel의 적당한 값을 mapping시키는 것을 의미한다. 쉽게 생각하면 네트워크가 이미지를 기억하게끔 하는 Unet, AutoEncoder 구조를 생각하면 될 것 같다.
problem
- 기존의 나와있던 방식은 메모리 voxel grid를 생성해서 진행하였기에 저장 cost가 매우 컸다.
- MLP를 사용하여 encoding을 하는 진행하기도 했지만, 기존의 mesh data를 사용하지 않고서는 복잡한 과정이 불가능 했었다.
Neural Radiance Field Scene Representation
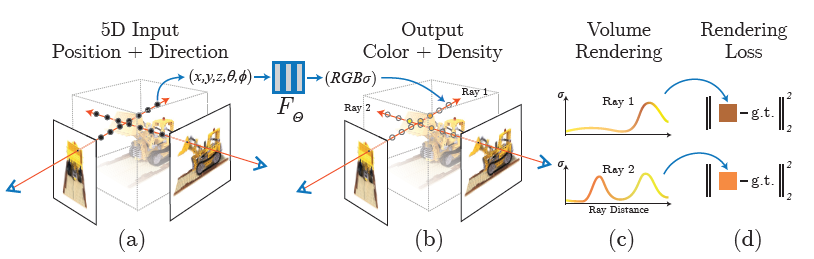
NeRF의 전체적인 절차는 밑의 그림과 같이 4개의 절차로 이루어져있다.
a: input으로 다양한 각도의 2d image를 사용 input
b: mlp()를 사용하여 color(RGB)와 density()를 예측 , rendering 진행
c: volume rendering을 진행하여 3d rendering이미지를 생성한다,
d: loss를 계산한다
무슨 의미인지 각각 살펴보자.
Classic volume rendering
Volume Ray Casting
Nerf에서는 Ground Truth로 classic volume rendering 를 사용한다.
volume rendering으로 구하는 Expected Color 은 다음과 같이 정의 된다.
,where
식을 자세히 살펴보기 전 notation부터 정리를 해보면
: camera ray
: expected rendering color
: predict volume rendering color
: camera ray 위의 관심있는 부분의 시작점
: camera ray 위의 관심있는 부분의 끝점
: 객체의 color
: volume density
: density는 camera ray 를 input으로 하는 function
장애물을 만나지 않고 로 갈 확률
각각을 기하학적으로 이해하는 것이 좋다. 우선 밑의 그림을 보자
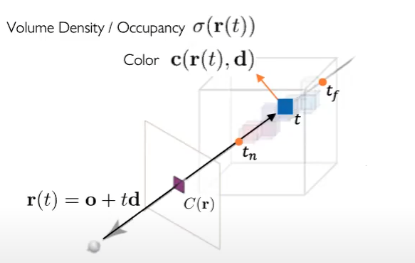
camera ray 로 정의되는데, 여기서 는 객체를 바라보는 시작점(카메라 렌즈로 생각하면 된다) 는 원점 에서 바라본 방향 벡터를 의미한다. 결국 객체에 대하여 camera ray 라는 녀석은 원점으로부터 바라본 벡터 위의 한 점을 의미한다.
그림을 보면 우리가 관심있는 영역(객체) ~ 의 범위에서 라는 시점에서의 volume density와 color c를 계산할 수 있다. 는 Uniform Density, Voxel-based Density, Signed Distance Field, Implicit Function등의 기법을 사용하여 계산가능 하고, 값은 [0,1]의 범위 값으로 나온다.
여기서 는 시점에서 입자들이 3차원 공간에서 얼만큼 차지하고 있는지를 의미하며,
는 시점에서 입자들이 만들어 내는 color를 의미한다. 와 를 알고 있다면 r(t)에서 바라본 rendering된 이미지의 Color 를 알 수 있다는 식이 이다.
여기서 한가지 알아얄 할 것은 을 구하기 위해서 integral을 사용하는데, Neural network에서 contineous data를 다루기에는 Memory cost 문제와 계산 복잡도 문제가 생긴다. 이를 해결하기 위해서 Sampling을 사용하여 근사하는데 , 이를 그림으로 보면 다음과 같다.
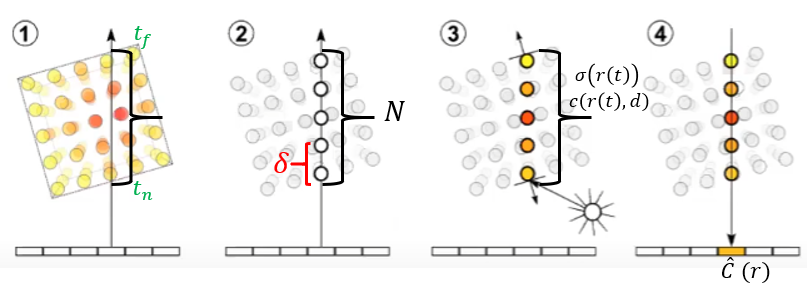
위의 camera ray를 위에서 봤을 때의 그림인데,
1 : ~의 연속 구간을 정한다.
2 : N개로 sampling을 진행한다.
3 : 각 시점 에 대해서 를 구한다.
4 : sampling한 것들에 대해서 를 구한다.
sampling을 진행하였을 때의 volume rendeing expected color 는 새롭게 근사할 수 있는데, 로 이 가 되었다.
continuous data의 경우 를 사용하는데, sampling을 진행할 경우는 를 사용하는 것을 볼 수 있다.
새로운 notation이 생겼는데 는 다음과 같이 정의 되는데, : 즉, sampling의 사이의 간격을 의미한다 (그림(2)확인)
위에서 설명하지 않은 마지막 term 에 대해서 확인할 수 있는데 위에서 정리하기론,
어떠한 particle(입자)도 만나지 않고 로 갈 확률이었다. 우선 exp(-x)의 그래프 부터 살펴보자
위의 지수 함수를 바탕으로 이해를 해보면, 는 값이 커질 수록 값이 작아진다. 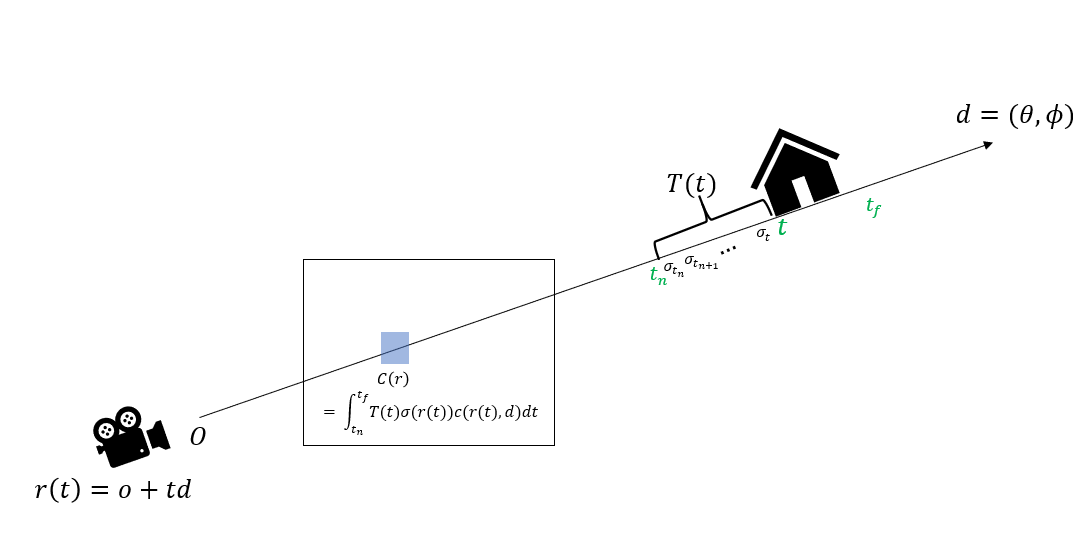 즉, 다음과 같은 그림으로 이해할 수 있는데, 는 바라보기를 원하는 시점 ~ 까지 모든 density들의 합이었고, 들이 크면 클 수록 는 작아졌다. 위에서 정의하기를 이었다. 즉, density 이면 카메라 시점으로 부터 시점에서의 particle이 존재하지 않는 다는 뜻이고, 이면 particle이 많다는 것을 의미한다.
즉, 다음과 같은 그림으로 이해할 수 있는데, 는 바라보기를 원하는 시점 ~ 까지 모든 density들의 합이었고, 들이 크면 클 수록 는 작아졌다. 위에서 정의하기를 이었다. 즉, density 이면 카메라 시점으로 부터 시점에서의 particle이 존재하지 않는 다는 뜻이고, 이면 particle이 많다는 것을 의미한다.
즉, density 가 크다는 것은 time step 시점에서 장애물을 만날 확률 이 크다는 것을 의미한다. 이를 토대로 식을 다시한번 상기해보면
expected Color 이라는 것은 결국 각 시점에 대해서 rat가 특정 영역동안 어떠한 particle도 만나지 않을 확률 x density x color의 누적 값이다.

sampling을 사용한 의 경우는 다음과 같이 정의 된다 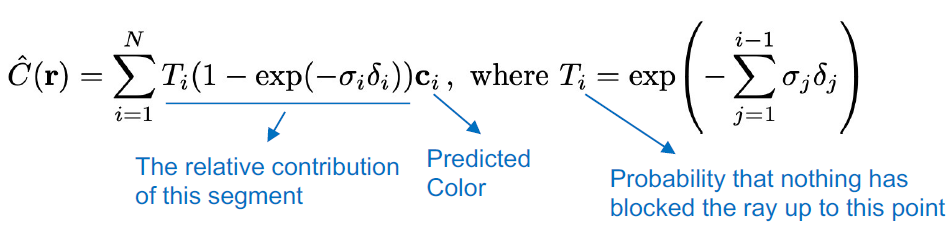
즉 우리의 모델 이란 것은 (장애물의 밀집도)가 낮고, (sample들의 거리)가 작을수록(sample들이 가까이 있을 수록) 밝기 가 더 선명해진다
if , ()
여기서 를 Alpha compositing이라고 부른다. 이는 컴퓨터 그래픽스에서 불투명한 객체를 합성하는 기술로서, 객체의 불투명도를 고려하여 최종적인 색상을 계산하는 방법이라고 한다.
Hierarchical volume sampling
위에서 는 연속적인 함수이기에 sampling을 사용하여 를 근사한다고 했다.
논문에서는 stratified sampling을 사용하여 uniform하게 sampling을 진행하였다.
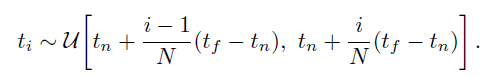
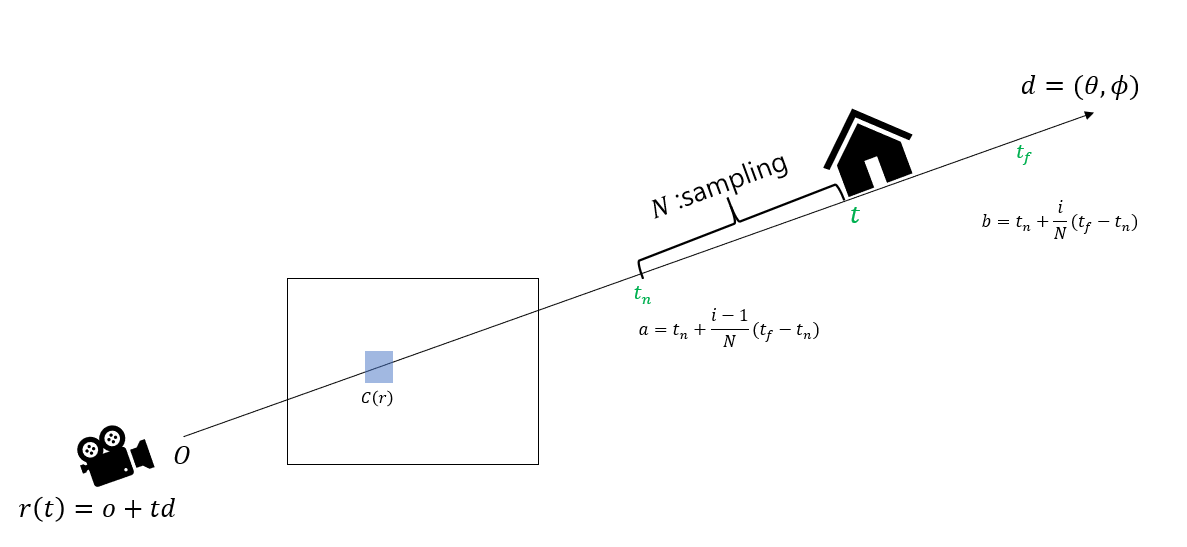
구간 a,b를 uniform하게 samling을 진행하는 것이다.
그러나 각 camera ray에 대해서 uniform하게 sampling하는 전략은 비효율적 이었다고 서술한다. free space(입자가 없는 부분)와 occluded regions(입자에 의해 완전히 가려져서 광선이 통과할 수 없는 부분)이 rendering에 도움을 주지 않기 때문인데, 이를 해결하고자 single network를 사용하는 것이 아니라 2개의 network를 최적화 하기로 결정한다.
2개의 네트워크를 각각 "coarse", "fine" network라고 부르는데,
- "coarse" network는 unifrom distribution을 사용하여 stratified sampling을 진행하여 전체 데이터의 분포를 학습,
- "fine" network는 Inverse transform sampling를 진행하여 각 ray에 대해서 편향된 분포를 학습한다.
여기서 inverse transform 과정은 다음과 같다.
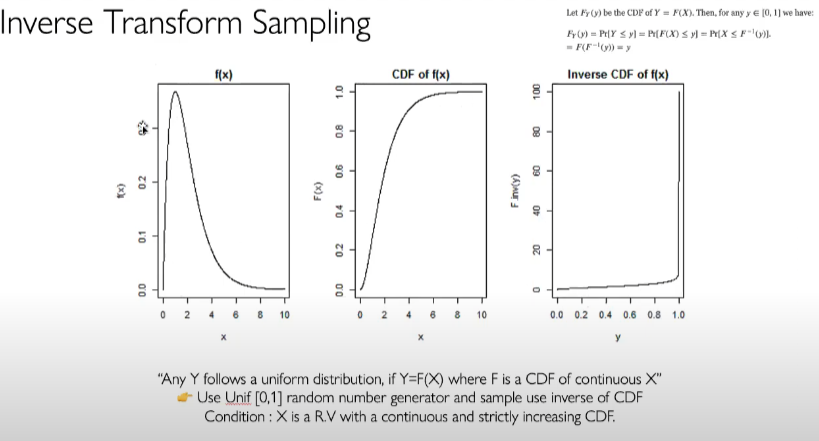
우선 sampling할 객체의 pdf를 구한다. 구한 pdf를 바탕으로 CDF를 계산하고, Inverse transform을 진행(맨 오른쪽 그림). Uniform distribution ~ [0,1]를 사용하여 Inverse transform CDF에서 sampling을 진행하면 밑의 그림처럼 free space와 occluded regions를 고려하여 sampling을 진행한다(구름의 뒤는 camera ray에서 보이지 않으므로 앞쪽에 sampling이 많이 된 것을 볼 수 있다.)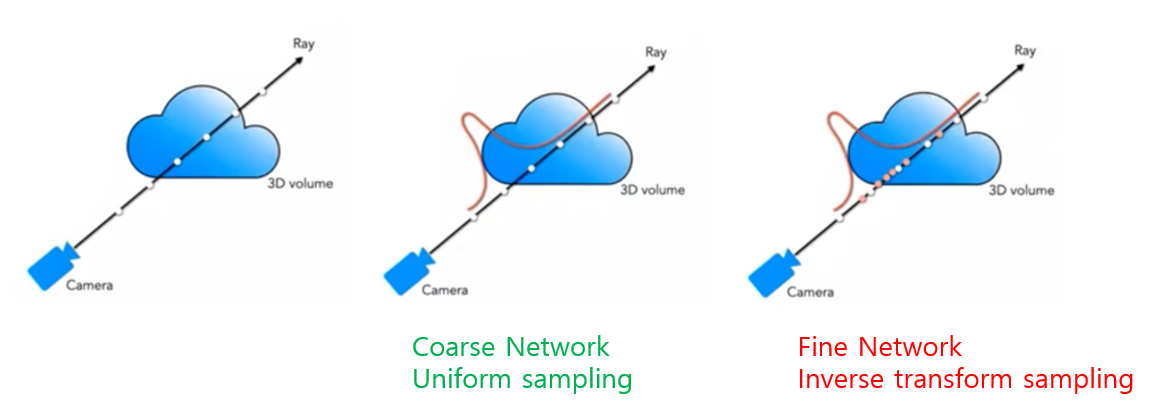
요약하면, model은 총 2개로 전반적인 분포에 대해서 학습을 진행하는 "coarse" network,
"fine" network로 구성되는데, 이를 각각 표현하면
-
"coarse" :
-
"fine" :
로 나타낼 수 있다. 여기서 로 normalize를 진행할 수 있다.주의
"fine" network의 경우 에서 가 아니라 를 사용하는데 이는 "fine" network가 전체의 부분도 고려하게끔 설정했기 때문이다.
View Dependent
논문에서는 Non-Lambertain effect를 주기 위해서 View Dependent를 사용한다.
Lambertain이란 완전한 빛을 표면으로 반사하는 효과이며 보는 각도에 상관없이 반사율이 동일한 것을 의미한다.
그렇다면 그 반대인 Non-Lambertain effect이란 보는 관점에 따라 명암이 다른 것을 원하는 것인데, 이를 구현하기 위해 Network를 2-step으로 나누었다. 전체적인 모델 은 밑의 그림처럼 동작하는데, 하나씩 보면
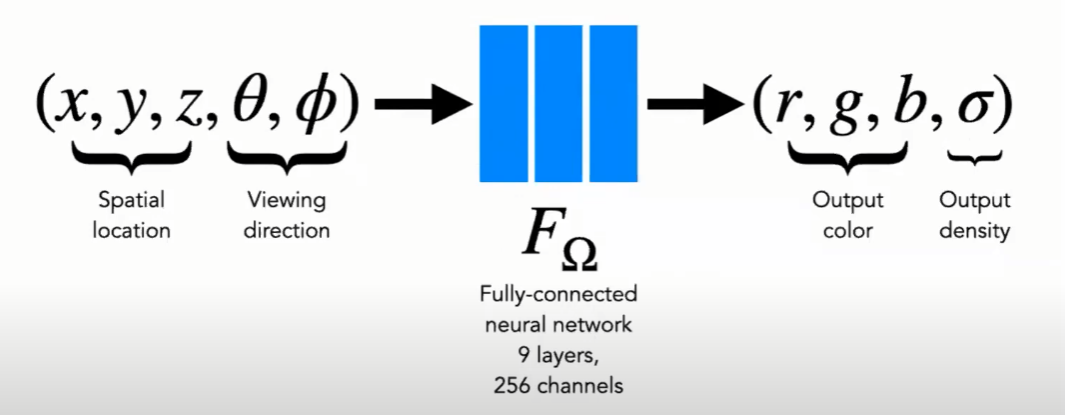
input으로 5D가 들어간다. 는 좌표를 의미하는 데이터이고, 는 카메라를 바라보는 관점을 설명한다. 이때 output은 와 를 output으로 나타내는데, 이를 풀어서 보면 다음과 같다.
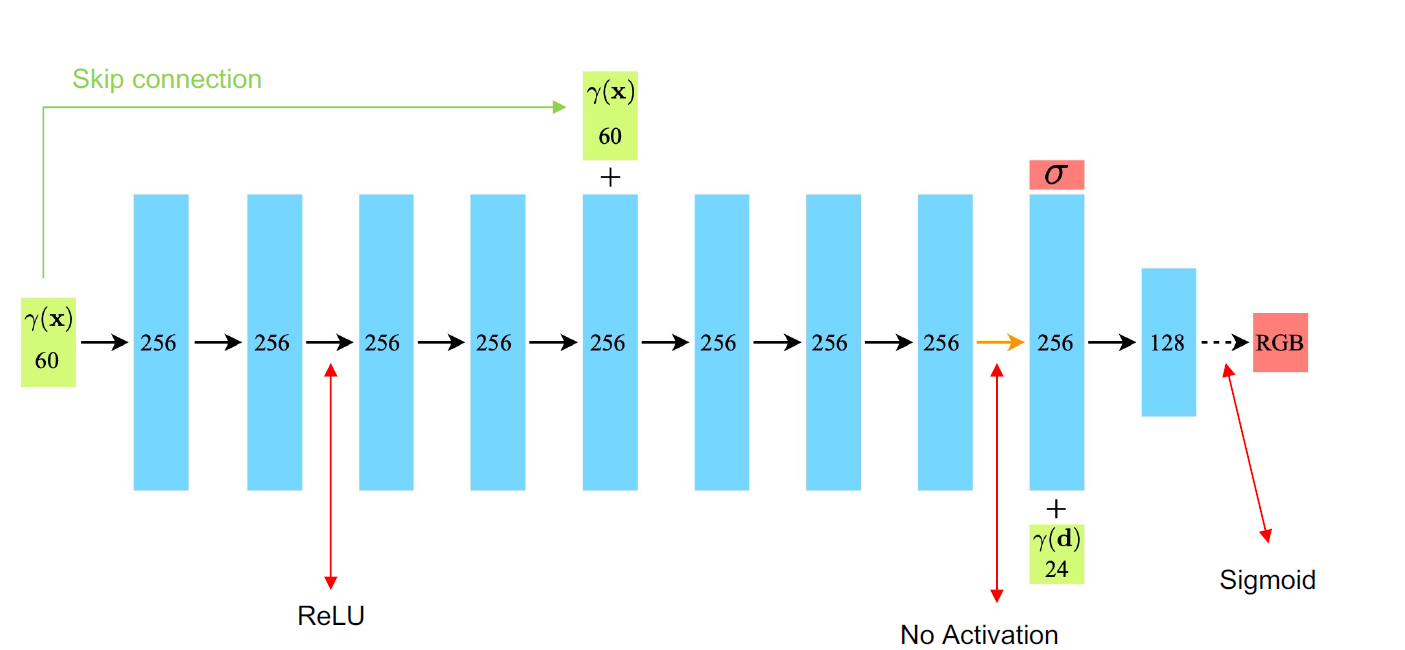
color의 정보만을 사용하여 를 예측하고, 8-layer에서 view-direction을 사용하여 color를 예측한다. 여기서 최종 output이 128인 이유는 color가 0~256이기 때문에 -값을 포함하여 -128~128의 output을 나오게끔 유도한 것이다.(sigmoid를 사용하면 -128~128 -> 0~1 (normalize된 0~256이 됨)
(skip connection 를 제외하고 모델 아키텍쳐를 자세히 살펴보면, input으로 을 positional encoding한 것을 input으로 집어 넣는다.
가 무엇인지는 밑에서 설명한다.
이렇게 하는 이유는 어디서 바라보든(view-direction) 상관없이 x,y,z의 좌표만으로 density를 표현하기 위해서이다.
- 좌표만 사용해서 density를 구한 결과

Positional encoding
high-resolution(모서리같은 detail)을 진행하기 위해서 각 camera ray의 양을 늘려보았지만, 비효율적이라는 실험결과가 있었다고 한다.
Positional encoding이란 개념은 Transformer에서도 확인할 수 있는데 NeRF의 Positional Endocing과 Transformer의 차이는
- Transformer : 모델의 구조가 Attention 만을 사용하기에 no recurrence하고 no convolution구조를 가지고 있다. 이에 어떤 data가 들어오더라도 input에 대하여 순서를 주기 위해서 Positional encoding을 사용하였다.
- NeRF: high-resolution(detail)을 표현하기 위해서 Positional encoding을 사용한다. input의 차원을 로 high-frequency로 변경하여 detail을 잘 표현할 수 있게 하는 것이 목적이다.
논문에서 제시한 Positional encoding은 다음과 같으며,
는 는 로 차원 임베딩을 진행한다
인 이유는 여기서 로 2차원인데 인 이유는 를 Cartesian viewing direction unit vector로 구하기 때문인데, Cartesian 좌표계는 3차원으로 표현이 된다고 한다.

Positional encoding을 사용하였을 때 detail 을 잘 설명하는 것을 볼 수 있고, View dependence를 사용하지 않았을 때 빛의 광도 표현을 잘 못하는 것을 볼 수 있다.
Loss
위에서 정의한 모델과 Hierarchical volume sampling에서 다뤘던 토대로 loss function을 정의하면된다.
total loss 두 색의 norm의 squared error를 계산하여 합한다.
implementation detail
= 64, = 128, Adam optimier에 5 x 10 -4 Learning rate와 5 x 10-5의 decay를 사용했다
R은 각 batch size마다 4096개의 ray를 사용했다고 한다.
평가 지표
여러 모델과 비교하여 진행하였는데,
각 평가지표는 영상 화질 손실양을 평가하기 위해 사용되는 지표이다.
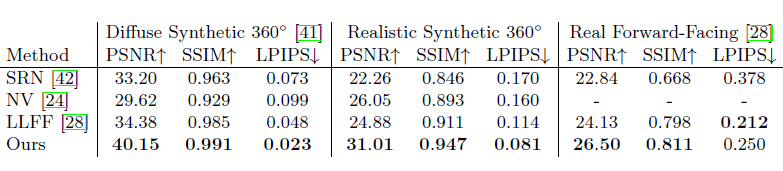
간략히 설명하면
PSNR(Peak Signal to Noise Ratio)
영상 화질 손실량으로, 얼마나 잘 복원했는가의 척도이다.
MSE값이 작을 수록 좋고, PSNR은 작을 수록 좋음
SSIM(Structural Similarity Index Measure)
얼마나 similarity를 가지는가? 에 대한 척도로 값이 높을 수록 좋다.
LPIPS(Learned Perceptual Image Patch similarity)
vgg의 feature에 대해서 유사도를 비교한 것으로, 낮을수록 feature domain의 유사도가 비슷한 것을 의미한다.
PSNR,SSIM
LPIPS
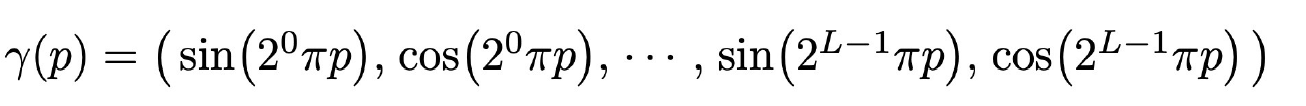

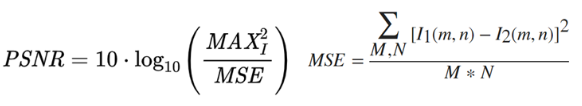
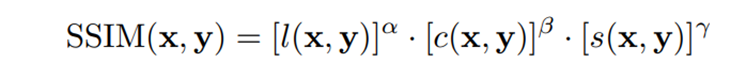
비밀 댓글입니다.