검정통계량의 확률분포

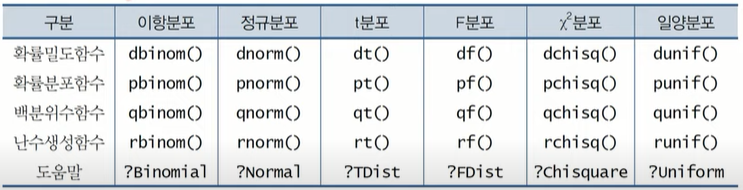
📌 이항분포

1. dbinom()
   dbinom(사건 발생 횟수, size=시행횟수, prob=사건 발생 확률)

> # 동전 10번 던졌을 때 숫자면이 7번 나타날 확률
> dbinom(7, size=10, prob=0.5)
[1] 0.1171875

2. pbinom()
   pbinom(누적 횟수, size=시행 횟수, prob=사건 발생 확률)

> # 동전 10번 던졌을 때 숫자면이 7번 나타날 확률
> dbinom(7, size=10, prob=0.5)
[1] 0.1171875

> dbinom(0:7, size=10, prob=0.5)
[1] 0.0009765625 0.0097656250 0.0439453125 0.1171875000 0.2050781250 0.2460937500 0.2050781250 0.1171875000

> sum(dbinom(0:7, size=10, prob=0.5)) # dbinom으로 구한 결과와 같음
[1] 0.9453125

3. lower.tail=FALSE
   누적확률의 반대편 확률 (윗 부분의 확률)

> # 동전 던지는 실험 10번 반복했을 때 숫자면이 8번 이상 나타날 확률
> pbinom(7, size=10, prob=0.5, lower.tail=FALSE)
[1] 0.0546875

4. 두 관측값 간의 확률

# 숫자면이 4번 이상 7번 이하 확률 = 7번 이하 - 3번 이하
> pbinom(7, size=10, prob=0.5) - pbinom(3, size=10, prob=0.5)
[1] 0.7734375

> # 벡터연산을 이용하여 두 관측값 간의 누적확률을 한 번에 구할 수 있다.
> pbinom(c(3, 7), size=10, prob=0.5)
[1] 0.1718750 0.9453125

> diff(pbinom(c(3, 7), size=10, prob=0.5))
[1] 0.7734375

5. rbinom()
   rbinom(난수 개수, size=, prob=)

> set.seed(1)
> rbinom(1, size=10, prob=0.5)
[1] 4
> rbinom(5, size=10, prob=0.5)
[1] 4 5 7 4 7

---

📌 정규분포

1. pnorm()
   pnorm(관측값, mean=, sd=)

> pnorm(110, mean=100, sd=10)
[1] 0.8413447

2. lower.tail=FALSE

> pnorm(110, mean=100, sd=10, lower.tail=FALSE)
[1] 0.1586553

3. 두 개의 관측값 간의 구간의 확률

# 90보다 크고 110보다 작거나 같은 확률 = 110 - 90
> pnorm(110, mean=100, sd=10) - pnorm(90, mean=100, sd=10)
[1] 0.6826895

> pnorm(c(90, 110), mean=100, sd=10)
[1] 0.1586553 0.8413447

> diff(pnorm(c(90, 110), mean=100, sd=10))
[1] 0.6826895

4. qnorm()
   qnorm(확률, mean=, sd=)

# mean=100, sd=10인 정규분포에서 누적확률 5% 이하 관측값
> qnorm(0.05, mean=100, sd=10)
[1] 83.55146

> # 전체의 95%에 대응되는 관측값
> qnorm(0.95, mean=100, sd=10)
[1] 116.4485

> # 확률을 벡터로 지정하면 동시에 여러 백분위수를 구할 수 있다.
> qnorm(c(0.05, 0.95), mean=100, sd=10)
[1]  83.55146 116.44854

# 신뢰구간 계산할 때 이용 가능
> qnorm(0.025)
[1] -1.959964
> qnorm(0.975)
[1] 1.959964

> qnorm(c(0.025, 0.975))
[1] -1.959964  1.959964

5. rnorm()
   rnorm(난수 개수, mean=, sd=)

> set.seed(1)
> rnorm(1, mean=100, sd=10)
[1] 93.73546

> rnorm(3, mean=c(-10, 0, 10), sd=1)
[1] -9.8163567 -0.8356286 11.5952808

> rnorm(6, mean=c(-10, 0, 10), sd=1)  # 재사용 규칙
[1] -9.6704922 -0.8204684 10.4874291 -9.2616753  0.5757814  9.6946116

---

📌 데이터 정규성 검정

1. shapiro.test()
   귀무가설 : 데이터의 분포가 정규분포를 따른다.

> set.seed(123)
> shapiro.test(rnorm(100, mean=100, sd=10))

	Shapiro-Wilk normality test

data:  rnorm(100, mean = 100, sd = 10)
W = 0.99388, p-value = 0.9349

# 유의수준 5% 하에서 귀무가설을 기각할 수 없으므로 데이터는 정규성을 만족한다.

> shapiro.test(runif(100, min=2, max=4))

	Shapiro-Wilk normality test

data:  runif(100, min = 2, max = 4)
W = 0.9454, p-value = 0.0004182

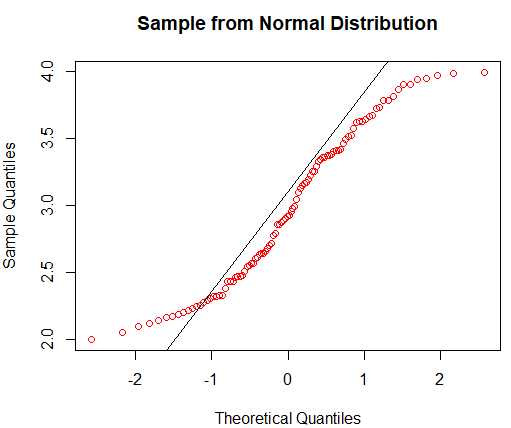
# 유의수준 5% 하에서 귀무가설을 기각하므로 데이터는 정규분포를 따르지 않는다.

2. qnorm()과 qqline()
   정규 Q-Q도표
   x축 : 이론적 정규분포로 생성된 표본
   y축 : 실제 표본

> set.seed(123)
> qqnorm(rnorm(100, mean=100, sd=10), col='blue', main='Sample from Normal Distribution')
> qqline(rnorm(100, mean=100, sd=10))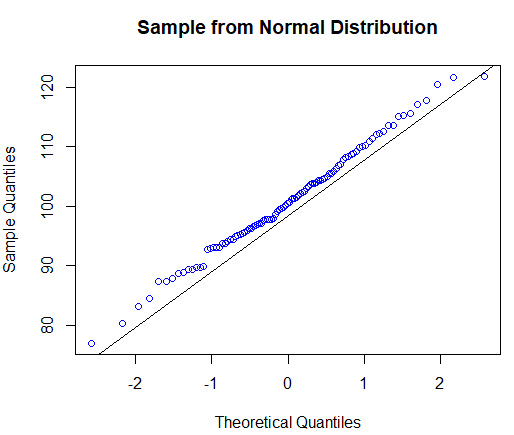

> qqnorm(runif(100, min=2, max=4), col='red', main='Sample from Normal Distribution')
> qqline(runif(100, min=2, max=4))