📌 t-test
t-분포
-
정규분포와 유사한 종 모양의 형태이며 정규분포에 비해 양쪽 꼬리 면접이 두텁다.
-
표본의 크기가 충분히 커지면 t분포와 정규분포는 거의 구별되지 않는다.
귀무가설 : 경영자의 혈압은 일반인과 같다.
대립가설 : 경영자의 혈압은 일반인과 다르다.
표본 : n=20, mean=135, sd=25
모집단 : mean=115
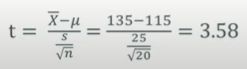
pt()
t분포에서 특정 t값에 대응되는 누적확률을 구할 수 있다.
pt(t값, df=n-1, loewr.tail=)
> pt(3.58, df=20-1) # 3.58 이하 누적확률
[1] 0.9990014
> pt(3.58, df=20-1, lower.tail=FALSE) # 3.58 이상 누적확률
[1] 0.0009986368
> pt(3.58, df=20-1, lower.tail=FALSE) * 2 # 양측검정 누적확률
[1] 0.001997274p-value=0.001997274 이므로 유의수준 0.05하에서 귀무가설을 기각한다. 즉, 경영자의 혈압은 일반인과 다르다.
qt()
특정확률에 대응되는 t값
qt(확룰, df=)
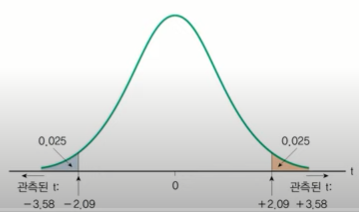
> qt(0.025, df=20-1, lower.tail=FALSE)
[1] 2.093024양측검정의 경우 절댓값으로 비교했을 때, 유의수준 0.05에 대응되는 t값보다 관측된 t값이 더 크면 귀무가설 기각한다.
표본으로부터 관측된 t-vale 3.58가 유의수준 0.05 하에서의 t-value는 2.093024보다 크다. 따라서 귀무가설을 기각한다. 즉, 경영자의 혈압은 일반인과 다르다.
📌 일표본 평균검정(one-sample t-test)
-
하나의 표본 데이터를 이용하여 모집단의 평균이 특정 값과 같은지를 검정한다.
-
표본집단이 특정 모집단과 일치하는지 아닌지 여부를 알고 싶을 때 사용한다.
> library(MASS)
> str(cats) # 고양이 성별에 따른 몸무게(Bwt)와 심장 무게(Hwt)
'data.frame': 144 obs. of 3 variables:
$ Sex: Factor w/ 2 levels "F","M": 1 1 1 1 1 1 1 1 1 1 ...
$ Bwt: num 2 2 2 2.1 2.1 2.1 2.1 2.1 2.1 2.1 ...
$ Hwt: num 7 7.4 9.5 7.2 7.3 7.6 8.1 8.2 8.3 8.5 ...귀무가설 : 고양이의 몸무게가 2.6kg이다.
대립가설 : 고양이의 몸무게가 2.6kg이 아니다.
t.test()
t.test(data, mu=평균)
추가 옵션으로 양측/단측검정과 신뢰구간 %를 지정할 수 있다.
- alternative = c("two.sided", "less", "greater")
- conf.level = 0.95
> t.test(cats$Bwt, mu=2.6)
One Sample t-test
data: cats$Bwt
t = 3.0565, df = 143, p-value = 0.002673
alternative hypothesis: true mean is not equal to 2.6
95 percent confidence interval:
2.643669 2.803553
sample estimates:
mean of x
2.723611
- mean of x (표본평균) = 2.723611
- t-value (t값) = 3.0565
- df (자유도) = 144-1 = 143
- p-value (유의확률) = 0.002673
- 95 percent confidence interval (95% 신뢰구간) = (2.643669, 2.083553)
p-value = 0.002673 이므로 귀무가설을 기각한다.
즉, 고양이의 몸무게가 2.6kg가 아니다.
prop.test
하나의 표본 데이터를 이용해서 모집단의 비율에 대한 통계적 검정한다.
prop.test(x=성공횟수, n=시행횟수, p=검정하고자 하는 비율)
귀무가설 : 팀의 승률이 50%보다 크다.
대립가설 : 팀의 승률이 50%보다 작다.
> prop.test(18, n=30, p=0.5, alternative="greater")
1-sample proportions test with continuity correction
data: 18 out of 30, null probability 0.5
X-squared = 0.83333, df = 1, p-value = 0.1807
alternative hypothesis: true p is greater than 0.5
95 percent confidence interval:
0.4344744 1.0000000
sample estimates:
p
0.6 유의수준 0.05하에서 귀무가설을 기각할 수 없다.
즉, 승률이 50%보다 크다.
📌 독립표본 평균검정(two-independent samples t-test)
-
두 개의 독립표본 데이터를 이용하여 각각 대응되는 두 개의 모집단 평균이 동일한지 검정한다.
-
두 집단이 서로 차이가 있는지 검정한다.
귀무가설 : 고양이 성별에 따라 몸무게에 차이가 없다.
대립가설 : 고양이 성별에 따라 몸무게에 차이가 있다.
> library(MASS)
> str(cats)
'data.frame': 144 obs. of 3 variables:
$ Sex: Factor w/ 2 levels "F","M": 1 1 1 1 1 1 1 1 1 1 ...
$ Bwt: num 2 2 2 2.1 2.1 2.1 2.1 2.1 2.1 2.1 ...
$ Hwt: num 7 7.4 9.5 7.2 7.3 7.6 8.1 8.2 8.3 8.5 ...t.test
t.test(formula=종속변수~독립변수, data=데이터셋)
> t.test(formula=Bwt ~ Sex, data=cats)
Welch Two Sample t-test
data: Bwt by Sex
t = -8.7095, df = 136.84, p-value = 8.831e-15
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.6631268 -0.4177242
sample estimates:
mean in group F mean in group M
2.359574 2.900000 p-value가 매우 작은 값이므로 귀무가설을 기각한다. 즉, 평균의 차이는 0이 아니다. 또는 95% 신뢰구간 내에 0이 포함되어 있지 않으므로 귀무가설을 기각한다.
> Bwt.f <- cats$Bwt[cats$Sex=="F"]
> Bwt.m <- cats$Bwt[cats$Sex=='M']
> mean(Bwt.f)
[1] 2.359574
> mean(Bwt.m)
[1] 2.9
> t.test(Bwt.f, Bwt.m)
Welch Two Sample t-test
data: Bwt.f and Bwt.m
t = -8.7095, df = 136.84, p-value = 8.831e-15
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.6631268 -0.4177242
sample estimates:
mean of x mean of y
2.359574 2.900000 위에서 검정한 결과와 같음을 알 수 있다.
prop.test
두 집단 간의 비율이 동일한지 검정한다.
귀무가설 : 폐질환자 대비 흡연자의 비율이 병원에 따라 차이가 없다.
대립가설 : 폐질환자 대비 흡연자의 비율이 병원에 따라 차이가 있다.
> patients <- c(86, 93, 136, 82) # 폐질환자수
> smokers <- c(83, 90, 129, 70) # 흡연자수
> smokers/patients # 폐질환자 대비 흡연자 비율
[1] 0.9651163 0.9677419 0.9485294 0.8536585
> prop.test(x=smokers, patients) # p-value가 매우 작으므로 귀무가설 기각한다. 즉, 병원에 따라 차이가 있다.
4-sample test for equality of proportions without continuity correction
data: smokers out of patients
X-squared = 12.6, df = 3, p-value = 0.005585
alternative hypothesis: two.sided
sample estimates:
prop 1 prop 2 prop 3 prop 4
0.9651163 0.9677419 0.9485294 0.8536585 p-value가 매우 작으므로 귀무가설 기각한다. 즉, 병원에 따라 차이가 있다.
📌 대응표본 평균검정 (paired-samples t-test)
- 두 표본이 쌍을 이루고 있는 경우에 쌍을 이룬 값은 서로 독립이 아니며, 두 개의 표본이 서로 독립이 아닌 모집단으로부터 추출되었을 때, 대응표본 평균검정을 이용하여 두 집단 간의 차이를 검정한다.
귀무가설 : 수면제에 따라 수면시간에 차이가 없다.
대립가설 : 수면제에 따라 수면시간에 차이가 있다.
> str(sleep)
'data.frame': 20 obs. of 3 variables:
$ extra: num 0.7 -1.6 -0.2 -1.2 -0.1 3.4 3.7 0.8 0 2 ...
$ group: Factor w/ 2 levels "1","2": 1 1 1 1 1 1 1 1 1 1 ...
$ ID : Factor w/ 10 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ...
> head(sleep)
extra group ID
1 0.7 1 1
2 -1.6 1 2
3 -0.2 1 3
4 -1.2 1 4
5 -0.1 1 5
6 3.4 1 6t.test
t.test(종속변수 ~ 독립변수, data=데이터셋, paired=TRUE)
> t.test(extra ~ group, data=sleep, paired=TRUE)
Paired t-test
data: extra by group
t = -4.0621, df = 9, p-value = 0.002833
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.4598858 -0.7001142
sample estimates:
mean of the differences
-1.58 p-value = 0.002833으로 귀무가설을 기각한다.
즉, 수면제에 따라 수면시간에 차이가 있다.
wide format vs long format
- wide format : 너비는 넓고, 길이는 짧게
- long format : 너비는 좁게, 길이는 길게
t.test() 함수에 종속변수, 독립변수 관계를 formular 형식으로 지정하기 위해서는 데이터셋이 롱포맷 형태로 되어 있어야 한다.
tidyr 패키지의 spread() 함수는
long format 데이터를 wide format 형태로 변경한다.
spread(long format, key=변수 목록 열, value=변수 값 열)
> sleep.wide <- spread(sleep, key=group, value=extra)
> sleep.wide
ID 1 2
1 1 0.7 1.9
2 2 -1.6 0.8
3 3 -0.2 1.1
4 4 -1.2 0.1
5 5 -0.1 -0.1
6 6 3.4 4.4
7 7 3.7 5.5
8 8 0.8 1.6
9 9 0.0 4.6
10 10 2.0 3.4
> t.test(sleep.wide$'1', sleep.wide$'2', paired=TRUE)
Paired t-test
data: sleep.wide$"1" and sleep.wide$"2"
t = -4.0621, df = 9, p-value = 0.002833
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.4598858 -0.7001142
sample estimates:
mean of the differences
-1.58앞의 결과와 같음을 알 수 있다.
