📌 다중회귀분석(multiple regression analysis)
- 두 개 이상의 연속형 독립변수를 이용하여 한 개의 연속형 종속변수를 예측한다.
- p개의 예측변수를 갖는 다중회귀모델
- y = B0 + B1 x1 + B2 x2 + ... = Bp xp
> str(mtcars)
'data.frame': 32 obs. of 11 variables:
$ mpg : num 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
$ cyl : num 6 6 4 6 8 6 8 4 4 6 ...
$ disp: num 160 160 108 258 360 ...
$ hp : num 110 110 93 110 175 105 245 62 95 123 ...
$ drat: num 3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
$ wt : num 2.62 2.88 2.32 3.21 3.44 ...
$ qsec: num 16.5 17 18.6 19.4 17 ...
$ vs : num 0 0 1 1 0 1 0 1 1 1 ...
$ am : num 1 1 1 0 0 0 0 0 0 0 ...
$ gear: num 4 4 4 3 3 3 3 4 4 4 ...
$ carb: num 4 4 1 1 2 1 4 2 2 4 ...
> mtcars <- mtcars[c("mpg", "hp", "wt", "disp", "drat")]
> head(mtcars)
mpg hp wt disp drat
Mazda RX4 21.0 110 2.620 160 3.90
Mazda RX4 Wag 21.0 110 2.875 160 3.90
Datsun 710 22.8 93 2.320 108 3.85
Hornet 4 Drive 21.4 110 3.215 258 3.08
Hornet Sportabout 18.7 175 3.440 360 3.15
Valiant 18.1 105 3.460 225 2.76회귀분석을 진행하기 전 변수의 요약통계량, 상관계수를 살펴보자.
> summary(mtcars)
mpg hp wt disp drat
Min. :10.40 Min. : 52.0 Min. :1.513 Min. : 71.1 Min. :2.760
1st Qu.:15.43 1st Qu.: 96.5 1st Qu.:2.581 1st Qu.:120.8 1st Qu.:3.080
Median :19.20 Median :123.0 Median :3.325 Median :196.3 Median :3.695
Mean :20.09 Mean :146.7 Mean :3.217 Mean :230.7 Mean :3.597
3rd Qu.:22.80 3rd Qu.:180.0 3rd Qu.:3.610 3rd Qu.:326.0 3rd Qu.:3.920
Max. :33.90 Max. :335.0 Max. :5.424 Max. :472.0 Max. :4.930
- mpg, hp 변수의 경우 Median < Mean : 오른쪽으로 긴 꼬리
- wt 변수의 경우 Mean < Median : 왼쪽으로 긴 꼬리
> cor(mtcars)
mpg hp wt disp drat
mpg 1.0000000 -0.7761684 -0.8676594 -0.8475514 0.6811719
hp -0.7761684 1.0000000 0.6587479 0.7909486 -0.4487591
wt -0.8676594 0.6587479 1.0000000 0.8879799 -0.7124406
disp -0.8475514 0.7909486 0.8879799 1.0000000 -0.7102139
drat 0.6811719 -0.4487591 -0.7124406 -0.7102139 1.0000000
- hp, wt, disp와는 음의 상관관계
- drat은 양의 상관관계
> library(car)
> windows(width=12, height=8)
> scatterplotMatrix(mtcars, pch=19, col="royalblue", cex=1.2,
+ regLine=list(metodh=lm, lty=1, lwd=3, col="salmon"),
+ smooth=list(smoother=loessLine, spread=FALSE,
+ lty.smooth=1, lwd.smooth=3, col.smooth="forestgreen"),
+ main="Car Performance")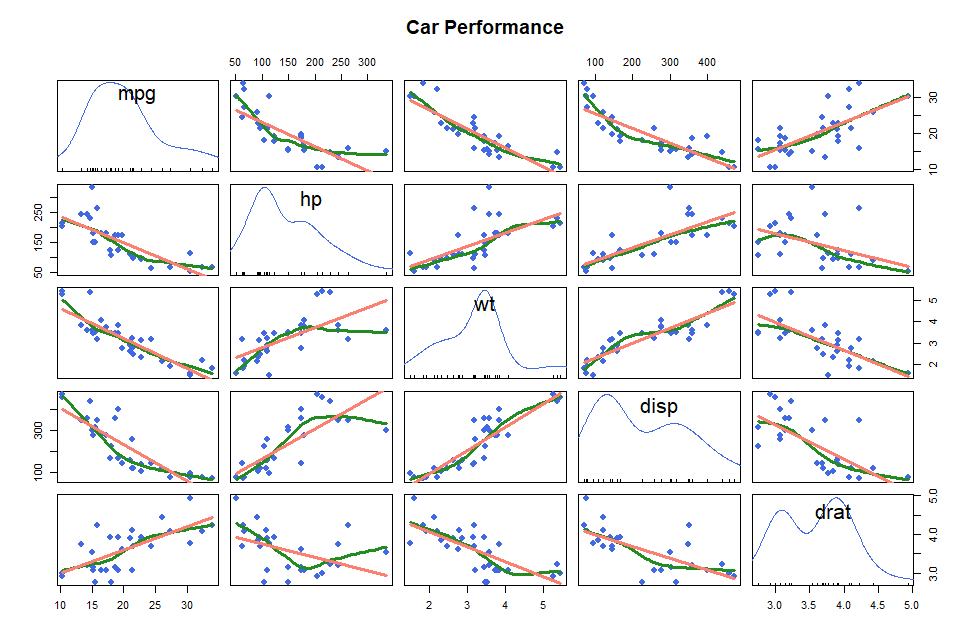
- mpg : 종속변수
- hp, wtm, disp, drat : 독립변수
📌 다중회귀분석
> mtcars.lm <- lm(mpg ~ hp + wt + disp + drat, data=mtcars)
> summary(mtcars.lm)
Call:
lm(formula = mpg ~ hp + wt + disp + drat, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.5077 -1.9052 -0.5057 0.9821 5.6883
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.148738 6.293588 4.631 8.2e-05 ***
hp -0.034784 0.011597 -2.999 0.00576 **
wt -3.479668 1.078371 -3.227 0.00327 **
disp 0.003815 0.010805 0.353 0.72675
drat 1.768049 1.319779 1.340 0.19153
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.602 on 27 degrees of freedom
Multiple R-squared: 0.8376, Adjusted R-squared: 0.8136
F-statistic: 34.82 on 4 and 27 DF, p-value: 2.704e-10
- F통계량의 p-value=2.704e-10이므로 다중회귀모델의 회귀식은 통계적으로 유의하다.
- hp, wt의 p-value=0.00576, 0.00327이므로 통계적으로 유의하다.
- disp, drat의 p-value=0.72675, 0.19153이므로 통계적으로 유의하지 않다. => mpg와 관련성이 없을 수도 있다.
- Multiple R-suared=0.8376, 83.76%의 설명력을 갖는다.
- Adjusted R-squared=0.8136, 81.36% 설명력을 갖는다.
예측변수가 표본 크기에 비해 많으면 과적합될 가능성이 높아진다. => 일반화 가능성이 떨어진다.
회귀계수만을 보고 어느 변수가 종속변수에 더 큰 기여를 하는지는 알 수 없다. 독립변수의 단위가 서로 달라서 직접적인 비교가 어렵기 때문이다.
📝 표준화게수 B(Beta)
변수 간의 비교를 위해 사용할 수 있는 것은 표준화계수이다.
독립변수와 종속변수를 표준점수로 변환하여 회귀분석 진행한다.
Beta는 종속변수에 대한 독립변수의 영향력을 비교할 때 유용하다. (측정 단위가 통일 되었기 때문)
> mtcars.lm2 <- lm(scale(mpg) ~ scale(hp) + scale(wt) + scale(disp) + scale(drat), data=mtcars)
> summary(mtcars.lm2)
Call:
lm(formula = scale(mpg) ~ scale(hp) + scale(wt) + scale(disp) +
scale(drat), data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-0.58201 -0.31611 -0.08391 0.16295 0.94382
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.397e-17 7.633e-02 0.000 1.00000
scale(hp) -3.957e-01 1.319e-01 -2.999 0.00576 **
scale(wt) -5.649e-01 1.751e-01 -3.227 0.00327 **
scale(disp) 7.846e-02 2.222e-01 0.353 0.72675
scale(drat) 1.569e-01 1.171e-01 1.340 0.19153
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4318 on 27 degrees of freedom
Multiple R-squared: 0.8376, Adjusted R-squared: 0.8136
F-statistic: 34.82 on 4 and 27 DF, p-value: 2.704e-10이제 회귀계수의 크기를 직접적으로 비교할 수 있다.
wt > hp > drat> disp 순으로 mpg에 영향을 미친다.
> library(QuantPsyc)
> lm.beta(lm(mpg ~ hp + wt + disp + drat, data=mtcars))
hp wt disp drat
-0.39569926 -0.56491388 0.07845695 0.15685187wt > hp > drat> disp 순으로 mpg에 영향을 미친다.
