📌 독립성 검정(independence test)
두 범주형 변수가 서로 독립인지 검정
독립이라는 것은 두 변수가 서로 관련이 없다는 것을 의미
귀무가설 : 두 변수는 독립이다.
대립가설 : 두 변수는 독립이 아니다.
- Class : 등급 (1등실, 2등실, 3등실, 선원)
- Sex : 성별
- Age : 나이
- Survived : 생존 여부
> str(Titanic)
'table' num [1:4, 1:2, 1:2, 1:2] 0 0 35 0 0 0 17 0 118 154 ...
- attr(*, "dimnames")=List of 4
..$ Class : chr [1:4] "1st" "2nd" "3rd" "Crew"
..$ Sex : chr [1:2] "Male" "Female"
..$ Age : chr [1:2] "Child" "Adult"
..$ Survived: chr [1:2] "No" "Yes"
> head(Titanic)
, , Age = Child, Survived = No
Sex
Class Male Female
1st 0 0
2nd 0 0
3rd 35 17
Crew 0 0
, , Age = Adult, Survived = No
Sex
Class Male Female
1st 118 4
2nd 154 13
3rd 387 89
Crew 670 3
, , Age = Child, Survived = Yes
Sex
Class Male Female
1st 5 1
2nd 11 13
3rd 13 14
Crew 0 0
, , Age = Adult, Survived = Yes
Sex
Class Male Female
1st 57 140
2nd 14 80
3rd 75 76
Crew 192 20다차원 테이블
다차원 테이블을 이용해서 독립성 검정을 하기 위해 검정하는 변수로 이루어진 2차원 형태 테이블로 변환하는 과정이 필요하다.
> Titanic.margin <- margin.table(Titanic, c(4, 1))
> Titanic.margin
Class
Survived 1st 2nd 3rd Crew
No 122 167 528 673
Yes 203 118 178 212열의 비율의 합이 100%가 되도록 만들어준다.
> addmargins(Titanic.margin)
Class
Survived 1st 2nd 3rd Crew Sum
No 122 167 528 673 1490
Yes 203 118 178 212 711
Sum 325 285 706 885 2201
> prop.table(addmargins(Titanic.margin, 2), 2)
Class
Survived 1st 2nd 3rd Crew Sum
No 0.3753846 0.5859649 0.7478754 0.7604520 0.6769650
Yes 0.6246154 0.4140351 0.2521246 0.2395480 0.3230350
> # 열의 합이 100% 라는 것을 보여줌
> addmargins(prop.table(addmargins(Titanic.margin, 2), 2), 1)
Class
Survived 1st 2nd 3rd Crew Sum
No 0.3753846 0.5859649 0.7478754 0.7604520 0.6769650
Yes 0.6246154 0.4140351 0.2521246 0.2395480 0.3230350
Sum 1.0000000 1.0000000 1.0000000 1.0000000 1.0000000 승객 구분에 따라 생존율에 차이가 있는지 검정해보자.
> chisq.test(Titanic.margin)
Pearson's Chi-squared test
data: Titanic.margin
X-squared = 190.4, df = 3, p-value < 2.2e-16귀무가설을 기각한다. 승객 구분에 따라 생존율에 차이가 있다.
만약 귀무가설을 기각하게 된다면 이들 간의 관련성을 평가할 수 있다.
> library(vcd)
> assocstats(Titanic.margin)
X^2 df P(> X^2)
Likelihood Ratio 180.9 3 0
Pearson 190.4 3 0
Phi-Coefficient : NA
Contingency Coeff.: 0.282
Cramer's V : 0.294📊 모자이크 도표
shade=TRUE : 귀무가설을 기각하는 데에 있어서 누가 더 큰 기여를 하는 지 색상으로 구분해볼 수 있다.
> mosaic(Titanic.margin, shade=TRUE)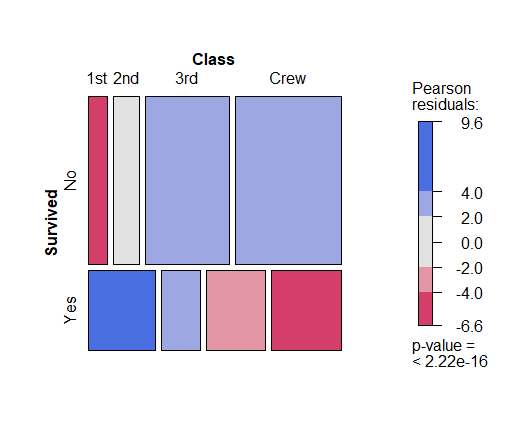
빨간색, 파란색 셀은 귀무가설을 기각하는데 크게 기여한다.
DataFrame
데이터프레임 형태의 데이터셋에서의 독립성 검정
- Sex : 성별
- Fold : 팔짱을 꼈을 때 어느 손이 위에 위치하는지
> str(survey)
'data.frame': 237 obs. of 12 variables:
$ Sex : Factor w/ 2 levels "Female","Male": 1 2 2 2 2 1 2 1 2 2 ...
$ Wr.Hnd: num 18.5 19.5 18 18.8 20 18 17.7 17 20 18.5 ...
$ NW.Hnd: num 18 20.5 13.3 18.9 20 17.7 17.7 17.3 19.5 18.5 ...
$ W.Hnd : Factor w/ 2 levels "Left","Right": 2 1 2 2 2 2 2 2 2 2 ...
$ Fold : Factor w/ 3 levels "L on R","Neither",..: 3 3 1 3 2 1 1 3 3 3 ...
$ Pulse : int 92 104 87 NA 35 64 83 74 72 90 ...
$ Clap : Factor w/ 3 levels "Left","Neither",..: 1 1 2 2 3 3 3 3 3 3 ...
$ Exer : Factor w/ 3 levels "Freq","None",..: 3 2 2 2 3 3 1 1 3 3 ...
$ Smoke : Factor w/ 4 levels "Heavy","Never",..: 2 4 3 2 2 2 2 2 2 2 ...
$ Height: num 173 178 NA 160 165 ...
$ M.I : Factor w/ 2 levels "Imperial","Metric": 2 1 NA 2 2 1 1 2 2 2 ...
$ Age : num 18.2 17.6 16.9 20.3 23.7 ...두 변수를 이용해 성별에 따라 팔짱을 꼈을 때 손 위치에 차이가 있는지 검정한다.
> chisq.test(survey$Fold, survey$Sex)
Pearson's Chi-squared test
data: survey$Fold and survey$Sex
X-squared = 2.5741, df = 2, p-value = 0.2761귀무가설을 기각하지 못 한다. 손 위치와 성별 간에 관련성이 없다.
