📌 이항 로지스틱 회귀분석(Binomial Logistic Regression Analysis)
- 결과변수(종속변수)가 이분형 범주를 가질 때 예측변수(독립변수)로부터 결과변수의 범주를 예측한다.
- 특정 사건이 발생할 확률을 직접 추정한다.
- 결과변수의 예측값은 0과 1 사이의 확률값을 가진다.
- 기준값(0.5)보다 크면 사건이 발생하고, 기준값 보다 작으면 사건이 발생하지 않는 것으로 예측한다.
ln(p / (1-p)) = B0 + B1x1 + B2x2 + ... + Bmxm
- x : 예측변수
- B : 회귀계수
- m : 예측변수의 개수
- 결과변수는 범주형 변수로서 1(사건 발생) 또는 0(사건 미발생)의 값을 갖기 때문에 결과 변수의 기대값(평균)은 항상0과 1 사이의 값을 가지며, 사건을 발생할 확률을 나타낸다.
- 로그 변환(로지스틱 변환)을 통해 예측변수의 선형결합으로 0과 1 사이의 결과변수 값을 나타낸다.
- 일반선형모델의 틀 내에서 살펴보면 링크함수는 ln(p - (1-p))이며, 결과변수 y의 확률분포는 이항분포이다.
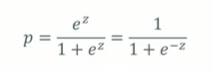
- p : 사건 발생 확률
- z = B0 + B1x1 + B2x2 + ... + Bmxm
- e : 자연로그
- 로지스틱 회귀선 : 예측변수와 결과변수는 S자 형태의 비선형 관계를 갖는다.
📌 로그 오즈, 오즈비
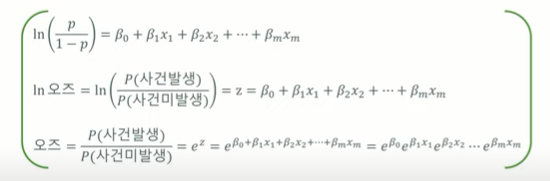
- p / (1-p)를 사건 발생의 오즈(odds)라고 하며, 사건이 발생할 가능성이 그렇지 않을 가능성의 몇 배인지를 나타낸다.
- 로지스틱 회귀모델은 오즈에 로그를 취한 로그오즈(log odds),
ln(p / (1-p))에 대한 선형모델을 정의한다. - 즉, 링크함수는 로그오즈
이동 통신 회사의 고객 이탈 데이터, 고객의 통화 특성과 이탈 여부
- chur : 이항 로지스틱 회귀모델의 결과변수(범주형 변수),
yes(고객 이탈 : 1), no(고객 미이탈 : 2)
> library(modeldata)
> data("mlc_churn")
> str(mlc_churn)
Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 5000 obs. of 20 variables:
$ state : Factor w/ 51 levels "AK","AL","AR",..: 17 36 32 36 37 2 20 25 19 50 ...
$ account_length : int 128 107 137 84 75 118 121 147 117 141 ...
$ area_code : Factor w/ 3 levels "area_code_408",..: 2 2 2 1 2 3 3 2 1 2 ...
$ international_plan : Factor w/ 2 levels "no","yes": 1 1 1 2 2 2 1 2 1 2 ...
$ voice_mail_plan : Factor w/ 2 levels "no","yes": 2 2 1 1 1 1 2 1 1 2 ...
$ number_vmail_messages : int 25 26 0 0 0 0 24 0 0 37 ...
$ total_day_minutes : num 265 162 243 299 167 ...
$ total_day_calls : int 110 123 114 71 113 98 88 79 97 84 ...
$ total_day_charge : num 45.1 27.5 41.4 50.9 28.3 ...
$ total_eve_minutes : num 197.4 195.5 121.2 61.9 148.3 ...
$ total_eve_calls : int 99 103 110 88 122 101 108 94 80 111 ...
$ total_eve_charge : num 16.78 16.62 10.3 5.26 12.61 ...
$ total_night_minutes : num 245 254 163 197 187 ...
$ total_night_calls : int 91 103 104 89 121 118 118 96 90 97 ...
$ total_night_charge : num 11.01 11.45 7.32 8.86 8.41 ...
$ total_intl_minutes : num 10 13.7 12.2 6.6 10.1 6.3 7.5 7.1 8.7 11.2 ...
$ total_intl_calls : int 3 3 5 7 3 6 7 6 4 5 ...
$ total_intl_charge : num 2.7 3.7 3.29 1.78 2.73 1.7 2.03 1.92 2.35 3.02 ...
$ number_customer_service_calls: int 1 1 0 2 3 0 3 0 1 0 ...
$ churn : Factor w/ 2 levels "yes","no": 2 2 2 2 2 2 2 2 2 2 ...- 데이터 전처리 작업
> churn <- mlc_churn- state : 고객의 거주 지역
- area_code : 거주 지역의 지역 코드
두 변수를 예측변수에서 제외시킨다.
> churn <- churn[, -c(1, 3)]
- 고객 이탈 : 사건 미발 (1)
- 고객 미이탈 : 사건 발생 (2)
관심 있는 사건은 고객 이탈이기 때문에 고객 이탈이 사건 발생으로 해석되도록 고객 미이탈(1), 고객 이탈(2)로 변환한다.
> churn$churn <- factor(ifelse(churn$churn=='no', 1, 2),
+ levels=c(1, 2),
+ labels=c('no', 'yes'))
$ churn : Factor w/ 2 levels "no","yes": 1 1 1 1 1 1 1 1 1 1 ...- 훈련 데이터 테스트 테이터 분류
- 훈련 데이터 : 로지스틱 회귀모델 생성에 사용
- 테스트 데이터 : 로지스틱 회귀모델 성능 예측에 사용
- 이미 무작위 배열이 되어 있으므로 2/3를 훈련 데이터로 1/3을 테스트 데이터로 사용한다.
- (5000 / 3) * 2 = 3333.333 이므로 3333개 데이터를 훈련 데이터로 사용
> churn.train <- churn[1:3333, ]
> churn.test <- churn[3334:5000, ]훈련 데이터와 테스트 데이터가 적절히 분할 되어 있는지 확인한다.
이탈 고객 비율 계산 후 비교한다.
> table(churn.train$churn)
no yes
2850 483
> prop.table(table(churn.train$churn)) # 이탈 고객 14.5%
no yes
0.8550855 0.1449145
> table(churn.test$churn)
no yes
1443 224
> prop.table(table(churn.test$churn)) # 이탈 고객 13.4%
no yes
0.8656269 0.1343731 이탈 고객 비율이 크게 다르지 않으므로 적절히 분할 되었다.
- 모델 생성
이항 로지스틱 회귀분석 glm() 함수
glm(종속변수 ~ 독립변수, data, family=이항분포 로짓)
> churn.logit <- glm(churn ~ ., data=churn.train, family=binomial(link='logit'))
> summary(churn.logit)
Call:
glm(formula = churn ~ ., family = binomial(link = "logit"), data = churn.train)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.1532 -0.5132 -0.3402 -0.1953 3.2528
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -8.6515638 0.7243142 -11.944 < 2e-16 ***
account_length 0.0008458 0.0013912 0.608 0.543199
international_planyes 2.0427543 0.1454974 14.040 < 2e-16 ***
voice_mail_planyes -2.0250146 0.5740840 -3.527 0.000420 ***
number_vmail_messages 0.0358803 0.0180108 1.992 0.046355 *
total_day_minutes -0.2441993 3.2742224 -0.075 0.940547
total_day_calls 0.0031962 0.0027612 1.158 0.247048
total_day_charge 1.5127081 19.2601862 0.079 0.937398
total_eve_minutes 0.8186945 1.6357258 0.501 0.616717
total_eve_calls 0.0010579 0.0027826 0.380 0.703817
total_eve_charge -9.5463678 19.2437266 -0.496 0.619840
total_night_minutes -0.1238287 0.8764906 -0.141 0.887650
total_night_calls 0.0006993 0.0028419 0.246 0.805628
total_night_charge 2.8338084 19.4769043 0.145 0.884319
total_intl_minutes -4.3377914 5.3009719 -0.818 0.413185
total_intl_calls -0.0929680 0.0250603 -3.710 0.000207 ***
total_intl_charge 16.3900316 19.6323938 0.835 0.403804
number_customer_service_calls 0.5135638 0.0392678 13.079 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2758.3 on 3332 degrees of freedom
Residual deviance: 2158.7 on 3315 degrees of freedom
AIC: 2194.7
Number of Fisher Scoring iterations: 6international_plan, voice_mail_plan가 범주형 변수이므로 자동으로 더미변수로 자동 변환되었다. 더미변수는 no, yes 중 첫 번째 no를 기준 범주로 한다.
1) 오즈비 계산
> exp(coef(churn.logit))
(Intercept) account_length international_planyes voice_mail_planyes number_vmail_messages
1.748532e-04 1.000846e+00 7.711821e+00 1.319919e-01 1.036532e+00
total_day_minutes total_day_calls total_day_charge total_eve_minutes total_eve_calls
7.833315e-01 1.003201e+00 4.539006e+00 2.267538e+00 1.001058e+00
total_eve_charge total_night_minutes total_night_calls total_night_charge total_intl_minutes
7.146035e-05 8.835312e-01 1.000700e+00 1.701012e+01 1.306535e-02
total_intl_calls total_intl_charge number_customer_service_calls
9.112226e-01 1.312503e+07 1.671236e+00
> - international_planyes가 1만큼 증가한다는 건 no에서 yes로 바뀐다는 걸 의미한다. 그때의 이탈/미이탈의 비가 7.7배 커진다.
- voice_mail_planyes가 1만큼 증가한다는 건 no에서 yes로 바뀐다는 걸 의미한다. 그때의 이탈/미이탈의 비가 0.13배 커진다. => 87% 감소한다.
- total_day_charge가 1만큼 증가한다는 건 오즈비는 4.54이다. 이탈/미이탈의 비가 4.5배 커진다.
- 만약 2만큼 증가한다는 건 4.539^2 = 20.6배 커진다.
2) 모델의 통계적 유의성 검정
- Null deviance: 2758.3 : 상수항만 포함된 예측모델의 이탈도
- Residual deviance: 2158.7 : 예측변수가 모두 포함된 이항 - 예측변수가 모두 포함된 이탈도가 더 작다.
- 자유도의 차이는 3332-3315=17이다.
📝 이탈도는 카이스퀘어 분포를 따른다.
자유도의 차이만큼 충분한 크기의 이탈도 차이가 있는지를 검정한다.
> pchisq(q=2758.3-2158.7, df=3332-3315, lower.tail=FALSE)
[1] 1.731898e-116
> pchisq(q=churn.logit$null.deviance - churn.logit$deviance,
+ df=churn.logit$df.null - churn.logit$df.residual,
+ lower.tail=FALSE)
[1] 1.757917e-116p-value=0에 가까운 값이므로 이탈도의 차이는 통계적으로 유의미한 차이이다. 위 두 코드는 방식만 다를 뿐 위와 같은 결과값이 나타난다.
- 고객 이탈 확률 예측
- type에 별도의 값을 지정하지 않으면 로그오즈로 계산한다.
- type='response' : 사건 발생 확률을 계산한다.
> churn.logit.pred <- predict(churn.logit, newdata=churn.test, type='response')
> head(churn.logit.pred)
3334 3335 3336 3337 3338 3339
0.07236813 0.05774332 0.22650409 0.15289153 0.07078500 0.05880824 - 이탈 / 미이탈 분류
0.5를 기준으로 0.5보다 크면 이탈 고객으로 0.5보다 작거나 같으면 미이탈 고객으로 분류한다.
> churn.logit.pred <- factor(churn.logit.pred > 0.5,
+ levels=c(FALSE, TRUE),
+ labels=c('no', 'yes'))
> head(churn.logit.pred)
3334 3335 3336 3337 3338 3339
no no no no no no
Levels: no yes
> table(churn.logit.pred)
churn.logit.pred
no yes
1595 7272명이 이탈 고객, 1595명이 미이탈 고객으로 분류되었다.
- 혼동행렬
실제 판정 결과와 로지스틱 회귀모델에 의한 예측 결과를 비교하기 위해 혼동행렬 생성한다.
> table(churn.test$churn, churn.logit.pred,
+ dnn=c('Actual', 'Predicted'))
Predicted
Actual no yes
no 1414 29
yes 181 43- 혼동행렬의 대각선의 값은 예측에 성공한 케이스를 나타낸다.
- 혼동행렬의 비대각선의 값은 정확한 분류에 실패한 케이스를 나타낸다. 181 + 29 = 210명
- 예측 정확도
> mean(churn.test$churn==churn.logit.pred) # 0.87
[1] 0.874025287.4%
📌 단계별 로지스틱 회귀모델
- 로지스틱 회귀모델 내에 유의하지 않은 예측모델을 제거하는 것이 성능 향상에 도움이 된다.
- step(로지스틱 회귀모델)
> churn.logit2 <- step(churn.logit)
> summary(churn.logit2)
Call:
glm(formula = churn ~ international_plan + voice_mail_plan +
number_vmail_messages + total_day_charge + total_eve_minutes +
total_night_charge + total_intl_calls + total_intl_charge +
number_customer_service_calls, family = binomial(link = "logit"),
data = churn.train)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.1204 -0.5133 -0.3375 -0.1969 3.2421
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -8.067161 0.515870 -15.638 < 2e-16 ***
international_planyes 2.040338 0.145243 14.048 < 2e-16 ***
voice_mail_planyes -2.003234 0.572352 -3.500 0.000465 ***
number_vmail_messages 0.035262 0.017964 1.963 0.049654 *
total_day_charge 0.076589 0.006371 12.022 < 2e-16 ***
total_eve_minutes 0.007182 0.001142 6.290 3.17e-10 ***
total_night_charge 0.082547 0.024653 3.348 0.000813 ***
total_intl_calls -0.092176 0.024988 -3.689 0.000225 ***
total_intl_charge 0.326138 0.075453 4.322 1.54e-05 ***
number_customer_service_calls 0.512256 0.039141 13.087 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2758.3 on 3332 degrees of freedom
Residual deviance: 2161.6 on 3323 degrees of freedom
AIC: 2181.6
Number of Fisher Scoring iterations: 61) 오즈비 계산
> exp(coef(churn.logit2))
(Intercept) international_planyes voice_mail_planyes number_vmail_messages total_day_charge
0.0003136727 7.6932116779 0.1348982797 1.0358905790 1.0795984333
total_eve_minutes total_night_charge total_intl_calls total_intl_charge number_customer_service_calls
1.0072083250 1.0860502564 0.9119442135 1.3856065987 1.6690530946 2) 모델의 통계적 유의성 검정
> pchisq(q=2758.293-2161.624, df=3332-3323, lower.tail=FALSE)
[1] 1.086172e-122
> pchisq(q=churn.logit2$null.deviance - churn.logit2$deviance,
+ df=churn.logit2$df.null - churn.logit2$df.residual,
+ lower.tail=FALSE)
[1] 1.086153e-122p-value=0에 가까운 값이므로 이탈도의 차이는 통계적으로 유의미한 차이이다.
3) 고객 이탈 확률 예측
> churn.logit2.pred <- predict(churn.logit2, newdata=churn.test, type='response')
> head(churn.logit2.pred)
3334 3335 3336 3337 3338 3339
no no no no no no
Levels: no yes4) 이탈 / 미이탈 분류
> churn.logit2.pred <- factor(churn.logit2.pred > 0.5,
+ levels=c(FALSE, TRUE),
+ labels=c('no', 'yes'))
> head(churn.logit2.pred)
3334 3335 3336 3337 3338 3339
no no no no no no
Levels: no yes
> table(churn.logit2.pred)
churn.logit2.pred
no yes
1590 7777명이 이탈 고객, 1590명이 미이탈 고객으로 분류되었다.
5) 혼동행렬
> table(churn.test$churn, churn.logit2.pred,
+ dnn=c('Actual', 'Predicted'))
Predicted
Actual no yes
no 1408 35
yes 182 426) 예측 정확도
> mean(churn.test$churn==churn.logit2.pred)
[1] 0.8698260.87%
때로는 관심 있는 특정 예측변수가 사건 발생 확률에 미치는 영향 살펴보는 것도 좋다.
예측변수 변화 수준에 따라 사건 발생 확률이 어떻게 달라지는가?
예측변수가 결과변수 확률에 미치는 영향
- 관심 있는 예측변수 값들이 포함된 데이터 셋 생성
- 값들을 변화시켜가며 어떻게 변화되는지 추정
ex) 고객의 서비스 센터 전화 횟수가 고객 이탈 확률에 미치는 영향에 관심이 있다.
서비스 센터 전화 횟수
> table(churn.test$number_customer_service_calls)
0 1 2 3 4 5 6 7
326 605 368 236 86 30 12 4- 0회 ~ 7회로 변화하는 8개 행의 데이터 프레임 생성
- 나머지 예측변수는 동일한 값으로 고정한다.
- 연속형 변수 : 평균값 고정
- 범주형 변수 : 가장 낮은 범주 유형으로 고정
> testdata <- data.frame(number_customer_service_calls=c(0:7),
+ international_plan='no',
+ voice_mail_plan='no',
+ number_vmail_messages=mean(churn.test$number_vmail_messages),
+ total_day_charge=mean(churn.test$total_day_charge),
+ total_eve_minutes=mean(churn.test$total_eve_minutes),
+ total_night_charge=mean(churn.test$total_night_charge),
+ total_intl_calls=mean(churn.test$total_intl_calls),
+ total_intl_charge=mean(churn.test$total_intl_charge))
> head(testdata)
number_customer_service_calls international_plan voice_mail_plan number_vmail_messages total_day_charge total_eve_minutes total_night_charge
1 0 no no 7.067786 30.82434 199.9492 8.974559
2 1 no no 7.067786 30.82434 199.9492 8.974559
3 2 no no 7.067786 30.82434 199.9492 8.974559
4 3 no no 7.067786 30.82434 199.9492 8.974559
5 4 no no 7.067786 30.82434 199.9492 8.974559
6 5 no no 7.067786 30.82434 199.9492 8.974559
total_intl_calls total_intl_charge
1 4.346731 2.784421
2 4.346731 2.784421
3 4.346731 2.784421
4 4.346731 2.784421
5 4.346731 2.784421
6 4.346731 2.784421
> testdata$prob <- predict(churn.logit2,
+ newdata=testdata,
+ type='response')
> testdata[c('number_customer_service_calls', 'prob')] # 고객 이탈 확률
number_customer_service_calls prob
1 0 0.05881547
2 1 0.09444949
3 2 0.14827168
4 3 0.22513913
5 4 0.32657688
6 5 0.44733309
7 6 0.57463916
8 7 0.69276138다른 예측변수들이 일정하다는 가정하에서의 예측확률 변화를 나타낸다.
📌 과산포
- 로지스틱 회귀분석을 진행할 때는 과산포의 문제가 발생할 수 있다.
- 결과변수의 실제 관측된 분산이 이항분포로부도 기대되는 분산보다 더 클 경우 발생한다.
- 과산포는 표준오차를 왜곡시켜 회귀계수의 유의성 검정을 부정확하게 만들 수 있다.
- glm(... family=quasibinomial())를 적용한다.
📝 과산포 확인하는 방법
- 로지스틱 회귀모델에서 이탈도와 자유도 간의 비율 확인
- 1을 넘으면 과산포 의심
> deviance(churn.logit2)/df.residual(churn.logit2)
[1] 0.65050380.65로 1보다 작기 때문에 과산포의 위험은 없다.
과산포 여부는 통계적으로 검정도 가능하다.
> fit.origin <- glm(churn ~ international_plan
+ + voice_mail_plan + number_vmail_messages
+ + total_day_charge + total_eve_minutes
+ + total_night_charge + total_intl_calls + total_intl_charge
+ + number_customer_service_calls,
+ family=binomial(),
+ data=churn.train)
> fit.overdis <- glm(churn ~ international_plan
+ + voice_mail_plan + number_vmail_messages
+ + total_day_charge + total_eve_minutes
+ + total_night_charge + total_intl_calls + total_intl_charge
+ + number_customer_service_calls,
+ family=quasibinomial(),
+ data=churn.train)
> pchisq(summary(fit.overdis)$dispersion * fit.origin$df.residual,
+ fit.origin$df.residual, lower.tail=FALSE)
[1] 0.08385493귀무가설 : 과산포 비율이 1이다.
p-value=0.084이므로 귀무가설을 기각할 수 없다.
즉, 과산포의 가능성은 작다.
