📌 선형회귀분석의 한계
- 선형회귀분석에서 결과변수는 연속형 변수이면서 정규분포를 따라야 한다.
- 현실에서 마주하는 문제에서는 결과변수가 범주형 변수일수도 있고 사건이 발생하는 획수일 수도 있으며, 이러한 변수는 정규분포를 따르지 않는다.
📌 선형회귀 모델
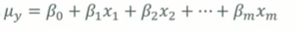
- 결과변수의 조건부 평균은 예측변수들의 선형결함으로 표현된다.
- 선형회귀모델은 예측변수 x들이 주어졌을 때 결과변수 y를 추정한다.
- y는 예측변수들이 사전에 주어졌을 때 y 분포의 평균이며 이런 의미에서 이를 조건부 평균이라고 한다.
📌 일반선형모델(Generalized Linear Model)
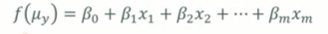
-
선형회귀모델을 확장한 정규분포를 따르지 않는 결과변수를 수용할 수 있는 일반회된 회귀모델
-
f(u)는 조건부 평균의 함수로서 링크함수(Link Function)라고 한다.
-
y는 정규분포뿐만 아니라 다른 확률분포를 따르는 것으로 가정할 수 있다.
-
링크함수와 확률분포를 지정함으로써 다양한 확장된 선형회귀모델을 생성할 수 있다.
-
표준적인 선형회귀모델은 일반선형모델의 한 특수한 경우이고, 확률분포가 정규분포이면 표준적인 선형회귀모델이 된다.
📌 로지스틱 회귀모델
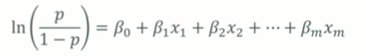
일반선형모델의 대표적인 예이다.
- 결과변수 : 범주형 변수
- 링크함수 : ln(p / (1-p))
- 확률분포 : 이항분포
📌 포아송 회귀모델
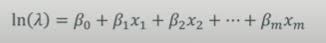
일반선형모델의 대표적인 예이다.
- 결과변수 : 횟수변수
- 링크함수 : ln(lambda)
- 확률분포 : 포아송분포
