📌 회귀모델 선택
회귀모델 선택은 모델의 예측정확도와 간명도를 바탕으로 한다.
- 예측 정확도 : 모델의 데이터 적합도
- 간명도 : 모델의 간결함과 재현성
- 예측변수가 많으면 모델의 데이터 적합도는 증가하나 재현성은 감소한다.
- 예측변수가 작으면 모델의 데이터 적합도는 감소하나 모델의 재현성은 증가한다.
- 예측정확도가 비슷한 두 대안모델이 있으면 일반적으로 가능한 단순한 모델을 선택하는 것이 바람직하다.
> str(mtcars)
'data.frame': 32 obs. of 11 variables:
$ mpg : num 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
$ cyl : num 6 6 4 6 8 6 8 4 4 6 ...
$ disp: num 160 160 108 258 360 ...
$ hp : num 110 110 93 110 175 105 245 62 95 123 ...
$ drat: num 3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
$ wt : num 2.62 2.88 2.32 3.21 3.44 ...
$ qsec: num 16.5 17 18.6 19.4 17 ...
$ vs : num 0 0 1 1 0 1 0 1 1 1 ...
$ am : num 1 1 1 0 0 0 0 0 0 0 ...
$ gear: num 4 4 4 3 3 3 3 4 4 4 ...
$ carb: num 4 4 1 1 2 1 4 2 2 4 ...📌 중첩된 모델 간의 적합도 비교
> mtcars.lm1 <- lm(mpg ~ hp + wt, data=mtcars)
> mtcars.lm2 <- lm(mpg ~ hp + wt + disp + drat, data=mtcars)
> anova(mtcars.lm1, mtcars.lm2)
Analysis of Variance Table
Model 1: mpg ~ hp + wt
Model 2: mpg ~ hp + wt + disp + drat
Res.Df RSS Df Sum of Sq F Pr(>F)
1 29 195.05
2 27 182.84 2 12.21 0.9016 0.4178귀무가설 : 두 개의 변수에 의해서 증가되는 R-square = 0이다.
p-value=0.4178 이므로 귀무가설을 기각하지 못한다. 통적으로 유의하지 않다. 따라서 hp와 wt만으로 구성된 회귀모델이 바람직하다.
> AIC(mtcars.lm1, mtcars.lm2)
df AIC
mtcars.lm1 4 156.6523
mtcars.lm2 6 158.5837AIC가 작을수록 우수한 모델이다.
lm1의 AIC=156.6523, lm2의 AIC=158.5837이므로 lm1이 더 우수한 모델이다.
📌 변수 선택
- 전진선택법(forward selection) : 상수항만을 갖는 모델로부터 시작하여 단계별로 한 개씩 중요한 독립변수를 모델에 포함시킨다.
- 후진선택법(backward selection) : 모든 독립변수가 포함된 모델로부터 시작하여 단계별로 한 개씩 덜 중요한 독립변수를 모델에서 제거한다.
- 단계선택법(stepwise selection) : 전진선택법과 후진선택법을 혼합한 방식이다.
새로 진입되거나 제거되는 변수가 더 이상 존재하지 않을 때까지 제거 과정을 반복한다.
step() 함수에 다중 회귀 모델 지정하여 변수 선택 진행
> mtcars.lm <- lm(mpg ~ hp + wt + disp + drat, data=mtcars)
> step(mtcars.lm, direction="backward")
Start: AIC=65.77
mpg ~ hp + wt + disp + drat
Df Sum of Sq RSS AIC
- disp 1 0.844 183.68 63.919
<none> 182.84 65.772
- drat 1 12.153 194.99 65.831
- hp 1 60.916 243.75 72.974
- wt 1 70.508 253.35 74.209
Step: AIC=63.92
mpg ~ hp + wt + drat
Df Sum of Sq RSS AIC
- drat 1 11.366 195.05 63.840
<none> 183.68 63.919
- hp 1 85.559 269.24 74.156
- wt 1 107.771 291.45 76.693
Step: AIC=63.84
mpg ~ hp + wt
Df Sum of Sq RSS AIC
<none> 195.05 63.840
- hp 1 83.274 278.32 73.217
- wt 1 252.627 447.67 88.427
Call:
lm(formula = mpg ~ hp + wt, data = mtcars)
Coefficients:
(Intercept) hp wt
37.22727 -0.03177 -3.87783 후진선택법을 사용했다. 각 단계마다 AIC 값을 가장 크게 감소시키는 변수가 제거된다.
최종적으로 만들어진 회귀 모델은 hp + wt를 독립변수로 사용한 회귀 모델이다.
📌 가능한 모든 회귀모델을 탐색하고 각 모델의 적합도를 평가
nbest = 독립변수의 각 subset 크기별로 탐색할 모델의 개수
brewer.pal(n, name) : 색상 개수, 색상 이름
> library(leaps)
> mtcars.regsubsets <-regsubsets(x=mpg ~ hp + wt + disp + drat, data=mtcars,
+ nbest=4)
> windows(width=10, height=8)
> library(RColorBrewer)
> plot(mtcars.regsubsets, scale="adjr2",
+ col=brewer.pal(9, "Pastel1"),
+ main="All Subsets Regression")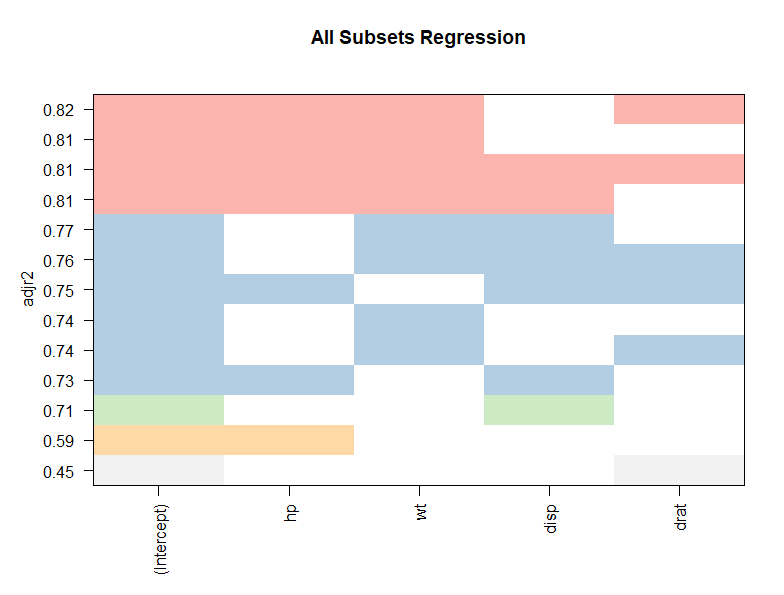
각 행은 하나의 회귀모델을 나타낸다.
- 1번째는 drat 변수를 독립변수로 갖는 회귀모델이다. 수정된 R-square=0.45이다.
- 2번째는 hp 변수를 독립변수로 갖는 회귀모델이다. 수정된 R-square=0.59이다.
- 3번째는 disp 변수를 독립변수로 갖는 회귀모델이다. 수정된 R-square=0.71이다.
- 밑에서 6번째는 wt 변수를 독립변수로 갖는 회귀모델이다. 수정된 R-square=0.74이다.
- 위에서 2번째는 hp와 wt 변수로 구성된 회귀 모델이다. 수정된 R-square=0.81이다.
subsets 회귀분석 그래프에 따르면 가장 적합도가 높은 회귀 모델은 그래프의 가장 위에 있는 것이다.
hp, wt, drat를 갖는 회귀모델이다. 수정된 R-square=0.82이다.
📌 수정된 R-square
> summary(mtcars.regsubsets)$adjr2
[1] 0.7445939 0.7089548 0.5891853 0.4461283 0.8148396 0.7658223 0.7444071 0.7308774 0.8194018 0.8082829 0.7603385 0.7509073 0.8135739📌 몇 번째 회귀모델이 가장 큰지
> which.max(summary(mtcars.regsubsets)$adjr2)
[1] 9📌 9번째 회귀모델의 회귀계수
coef(mtcars.regsubsets, 9)