회귀분석 가정과 진단, 회귀모델 수정

📌 회귀분석 가정과 진단, 회귀모델 수정

⭐ 회귀분석 가정 ⭐

1. 선형성(linearity) : 종속변수와 독립변수 간의 관계는 선형이다.
2. 정규성(normality) : 독립변수 값에 대해 대응되는 종속변수 값들의 분포는 정규분포이다.
3. 등분산성(homoscedasticity, equaltiry of variance) : 독립변수 값에 대해 대응되는 종속변수 값들의 분포는 모두 동일한 분산을 갖는다.
4. 독립성(independence) : 모든 관측값은 서로 독립이다.

> str(mtcars)
'data.frame':	32 obs. of  11 variables:
 $ mpg : num  21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
 $ cyl : num  6 6 4 6 8 6 8 4 4 6 ...
 $ disp: num  160 160 108 258 360 ...
 $ hp  : num  110 110 93 110 175 105 245 62 95 123 ...
 $ drat: num  3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
 $ wt  : num  2.62 2.88 2.32 3.21 3.44 ...
 $ qsec: num  16.5 17 18.6 19.4 17 ...
 $ vs  : num  0 0 1 1 0 1 0 1 1 1 ...
 $ am  : num  1 1 1 0 0 0 0 0 0 0 ...
 $ gear: num  4 4 4 3 3 3 3 4 4 4 ...
 $ carb: num  4 4 1 1 2 1 4 2 2 4 ...

📌 다중 회귀분석

> mtcars.lm <- lm(mpg ~ hp + wt + disp + drat , data=mtcars)
> plot(mtcars.lm)

총 4개의 진단 도표가 나타난다 Return 키로 확인할 수 있다.

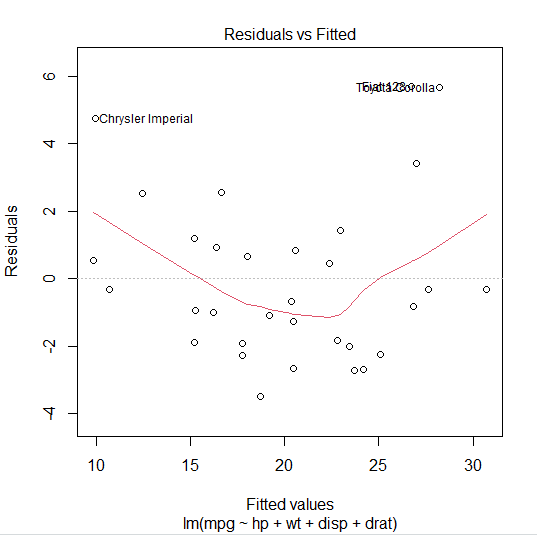
⭐ 첫 번째 그래프 : 선형성 ⭐

• 독립변수와 종속변수가 선형관계를 가지면 잔차와 예측값 간에는 어떠한 체계적 관계가 존재해서는 안 된다.
• 예측 가능한 패턴이 보이면 안 된다. 즉, 무작위적인 오차
• y는 잔차 x는 예측값
• 수평선을 중심으로 무작위적으로 배치되는 패턴을 보여아 선형성을 만족한다.
• 선형성 가정을 완벽히 충족하지는 못 한 것으로 보인다.

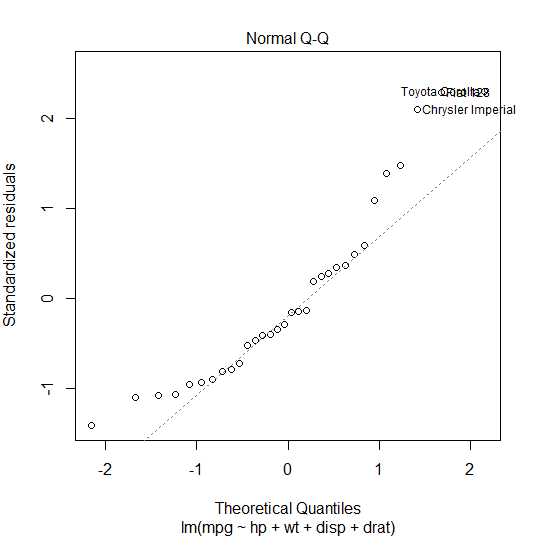
⭐ 두 번째 그래프 : 정규성 ⭐

• 정규분포라면 잔차는 평균 0의 정규분포를 따라야 한다.
• x는 이론적 정규분포 y는 실제 잔차이므로 직선의 형태가 대각선의 직선의 형태가 나타나야 정규성을 만족한다.
• 대각선을 벗어난 관측값들도 보이므로 온전히 정규성을 충족했다고 보이엔 어렵다.

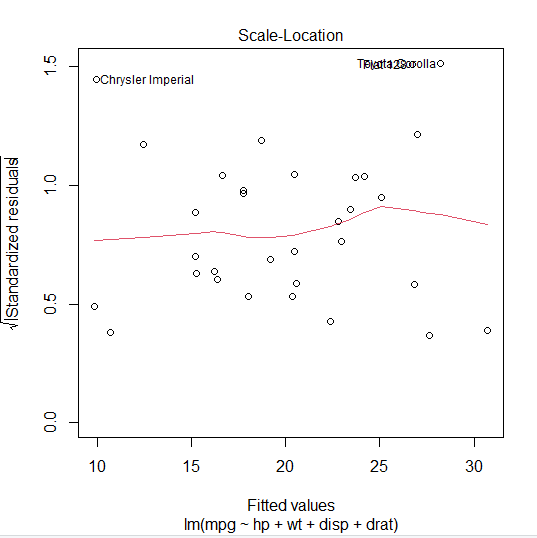
⭐ 세 번째 그래프 : 등분산성 ⭐

• y는 표준화 잔차의 루트 x는 예측값
• 등분산 가정을 충족한다면 무작위분포를 이뤄야 한다.
• 등분산성 가정을 충족한다.

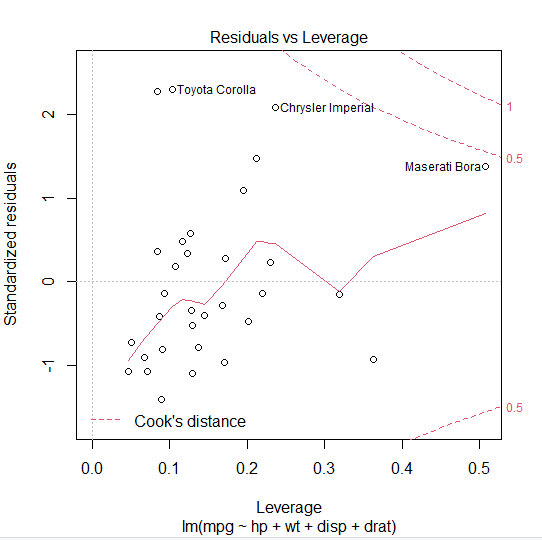
⭐ 네 번째 그래프 : 주의를 기울일 필요가 있는 관측값 ⭐

• 이상점, 영향점 식별
• 이상점은 y축을 기준으로 식별한다.
• 영향점은 쿡의 거리를 이용해 식별한다.
• 일반적으로 쿡의 거리가 1보다 큰 관측값을 영향점이라고 한다.

독립성은 진단 도표로는 확인할 수 없다.

📌 다중공선성(multicollinearity)

독립변수 간의 강한 선형관계

다중공선성이 존재할 경우 나타날 수 있는 현상 ❓

• 분산분석의 F값에 의해 회귀식의 전반적인 유의성이 확인되더라도 t값에 의한 개별 회귀계수에 대한 유의성이 나타나지 않는다.
• 회귀게수가 상식에 반하는 부호를 가진다.

• 다중공선성은 분산팽창지수(variance inflation factor, VIF)로 측정한다.
• VIF가 4를 넘으면 다중공선성이 존재하는지 점검할 필요가 있으며, 10을 넘으면 다중공선성이 존재할 가능성이 높다고 판단한다.
• VIF = 1 / (1 - R^2)

> library(car)
> vif(mtcars.lm)
      hp       wt     disp     drat 
2.894373 5.096601 8.209402 2.279547 

VIF가 10을 넘는 것은 보이지 않는다.

---

📌 회귀모델 수정

회귀모델 진단 결과로 회귀모델 가정이 위배되었다는 것을 알았을 때 회귀모델 수정 필요하다.

관측값 제거, 변수 변환, 변수 추가/제거

• 이상점/영향점 => 관측값 제거
• 선형적, 정규성, 등분산성 미충족 => 변수 변환
• 선형성의 가정을 위배 => 독리변수를 변환
• 정규성.등분산 가정을 위배 => 종속변수를 변환
• 다중공선성 => 변수 제거

⭐ 변수 변환 ⭐

원래의 변수 x를 x^lambda로 변환한다.

1. 정규성 가정 위배
   종속변수 변환

> powerTransform(mtcars$mpg)
Estimated transformation parameter 
mtcars$mpg 
0.02956537 

추정된 lambda=0.0296 => mpg를 mpg^0.0296로 대체한다.
0.0296은 0에 근접하므로 로그변환 ln(x)을 한다.

> summary(powerTransform(mtcars$mpg))
bcPower Transformation to Normality 
           Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
mtcars$mpg    0.0296           1      -1.0107       1.0698

Likelihood ratio test that transformation parameter is equal to 0
 (log transformation)
                             LRT df    pval
LR test, lambda = (0) 0.00310595  1 0.95556

Likelihood ratio test that no transformation is needed
                           LRT df    pval
LR test, lambda = (1) 3.212664  1 0.07307

가설검정 : lambda = 1 => x^1 이므로 즉, 변환을 하지 않는다.
p-value=0.07307로 귀무가설을 기각할 수 없다. 즉, 변수 변환이 필요하지 않다.

2. 선형성 가정 위배
   독립변수 변환

> boxTidwell(mpg ~ hp + wt, data=mtcars)
   MLE of lambda Score Statistic (z) Pr(>|z|)   
hp      -0.56824              2.3741 0.017592 * 
wt      -0.41743              2.7228 0.006473 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

iterations =  6 

hp=-0.56824, wt=-0.41743으로 대체한다.

p-value=0.017592와 0.006473으로 귀무가설을 기각한다.
즉, 변수 변환이 필요하다.

lambda가 -0.5에 근접하므로 hp^-0.5와 wt^-0.5으로 변환한다.

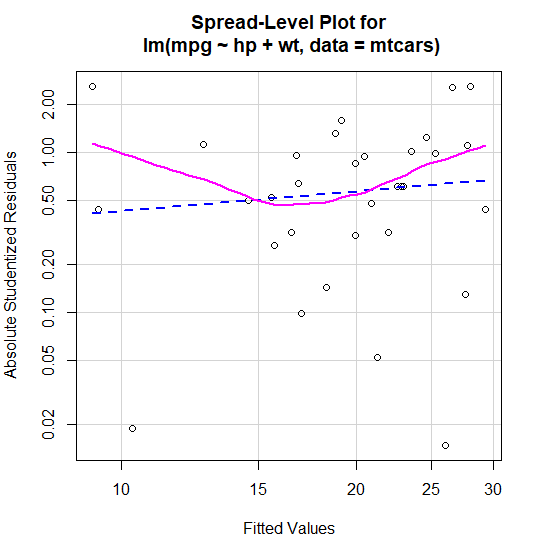
3. 등분산 가정 위배
   종속변수 변환

> spreadLevelPlot(lm(mpg ~ hp + wt, data=mtcars))

Suggested power transformation:  0.5853955

lambda=0.5853955 이므로 mpg^0.5로 대체한다.